这篇博客的内容摘自课本,针对课本中缺少的5道证明题,作为练习,给出证明。
算法运行时所需要的计算机时间资源的量称为时间复杂性。这个量应该集中反应算法的效率,并从运行该算法的实际计算机中抽象出来。换句话说,这个量应该是只依赖于要解的问题的规模、算法的输入和算法本身的函数。
如果分别用 N,I和A 表示算法要解的问题的规模、算法的输入和算法本身,而且用 T 表示时间复杂性,那么,应该有 T=T(N,I,A) 。通常 A 隐含在复杂性函数名中,因而将 T 简写为 T(N,I) 。
现在,时间复杂性分析的主要问题是如何将复杂性函数具体化,即对于给定的 N,I和A ,如何导出 T(N,I) 的数学表达式,来给出计算 T(N,I) 的法则。
根据 T(N,I) 的概念,它应该是算法在一台抽象的计算机上运行所需要的时间。设此抽象的计算机所提供的原运算有 k 种,它们分别记为 O1,O2,...,Ok 。又设每执行一次这些元运算所需要的时间分别为 t1,t2,...,tk 。对于给定的算法 A ,设经统计,用到元运算 Oi 的次数为 ei,i=1,2,...,k 。很清楚,对于每一个 i,1≤i≤k,ei 是 N和I 的函数,即 ei=ei(N,I)
。因此有
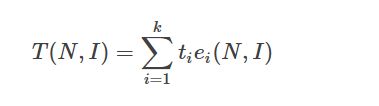
式中, ti(i=1,2,...,k ),是与 N和I 无关的常数。
显然,不可能对规模为 N 的每一种合法的输入都去统计 ei(N,I),i=1,2,...,k 。因此 T(N,I) 的表达式还要进一步简化,或者说,只能在规模为 N 的某些或某类有代表性的合法输入中统计相应的 ei,i=1,2,...,k ,评价其时间复杂性。通常只考虑三种情况下的时间复杂性,即最坏情况、最好情况和平均情况下的时间复杂性,并分别记为 Tmax(N)、Tmin(N)和Tavg(N) 。在数学上有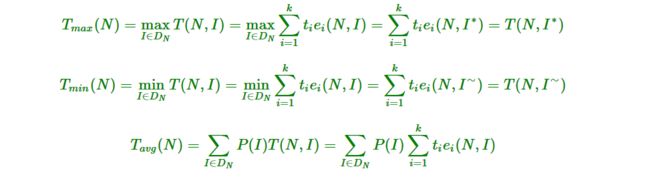
式中, DN 是规模为 N 的合法输入的集合; I∗ 是 DN 中使 T(N,I∗) 达到 Tmax(N) 的合法输入;I∼ 是 DN 中使 T(N,I∼) 达到 Tmin(N) 的合法输入;而 P(I) 是在算法的应用中出现输入 I 的概率。
以上三种情况下的时间复杂性从某一角度反应算法的效率,各有局限性,也各有各的用处。实践表明,可操作性最好且最有实际价值的是最坏情况下的时间复杂性。
为了简化算法复杂性的分析,下面引入复杂性渐近性态的概念。
设 T(N) 是前面所定义的关于算法A的复杂性函数。一般来说,当 N 单调递增且趋于 ∞ 时, T(N) 也将单调增加且趋于 ∞ 。对于 T(N) ,如果存在 T∼(N) ,使得当 N→∞ 时有 T(N)−T∼(N))/T(N)→0 ,那么,就说 T∼(N) 是 T(N) 当 N→∞ 时的渐近性态,或称 T∼(N) 为算法 A 当 N→∞ 的渐近复杂性,而与 T(N) 相区别。
因为在数学上, T∼(N) 是 T(N) 当 N→∞ 时的渐近表达式。直观上, T∼(N) 是 T(N) 中略去低阶项所留下的主项,所以它无疑比 T(N) 来得简单。比如当 T(N)=3N2+4NlogN+7 时,T∼(N) 的一个答案是 3N2 ,因为这时有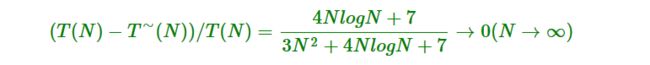
显然, 3N2 比 3N2+4NlogN+7 简单多了。
由于当 N→∞ , T(N) 渐近于 T∼(N) ,我们有理由用 T∼(N) 来代替 T(N) 作为算法 A 在 N→∞ 时的复杂性的度量。而且由于 T∼(N) 明显比 T(N) 简单,这种替换明显的是对算法复杂性分析的一种简化。进一步考虑到分析算法的复杂性的目的在于比较解同一个问题的两个不同算法的效率。而当要比较的两个算法的渐近复杂性的阶不同时,只要能确定出各自的阶,就可以判定出哪一个算法的效率高。换句话说,这时的渐近复杂性分析只要关心 T∼(N) 的阶就够了,不必关心包含在 T∼(N) 中的常数因子。所以,假设算法中用到的所有不同的元运算各执行一次所需要的时间都是一个单位时间。与此同时,引出以下渐近意义下的记号 O,Ω,θ和o 。
以下设 f(N)和g(N) 是定义在正数集上的正函数。
如果存在正的常数 C 和自然数 N0 ,使得当 N≥N0 时有 f(N)≤Cg(N) ,则称函数 f(N) 当 N 充分大时上有界,且 g(N) 是它的一个上界,记为 f(N)=O(g(N)) 。这时还说 f(N) 的阶不高于 g(N) 的阶。
举几个例子:
(1)因为对于所有的 N≥1 有 3N≤4N ,所以有 3N=O(N) ;
(2)因为当 N≥1 时有 N+1024≤1025N ,所以有 N+1024N=O(N) ;
(3)因为当 N≥10 时有 2N2+11N−10≤3N3 ,所以有 2N2+11N−10=O(N2);
(4)因为对所有 N≥1 有 N2≤N3 ,所以有 N2=O(N3) ;
(5)作为一个反例, N3≠O(N2) 。因为若不然,则存在正的常数 C 和自然数 N0 ,使得当 N≥N0有N3≤CN2 ,即 N≤C 。显然,当 N=max{N0,⌊C⌋+1} 时这个不等式不成立,所以N3≠O(N2) 。
按照符号 O 的定义,容易证明它有如下运算规则:
(1)O(f)+O(g)=O(max(f,g));
(2)O(f)+O(g)=O(f+g) ;
(3)O(f)O(g)=O(fg) ;
(4)如果g(N)=O(f(N)) ,则 O(f)+O(g)=O(f) ;
(5)O(Cf(N))=O(f(N)) ,其中 C 是一个正的常数;
(6)f=O(f) 。
下面仅给出规则(1)的证明过程,其余类似。
设 F(N)=O(f) 。根据符号 O 的定义,存在正常数 C1 和自然数 N1 ,使得对所有的 N≥N1 ,有 F(N)≤C1f(N) 。
类似地,设 G(N)=O(g) ,则存在正的常数 C2 和自然数 N2 ,使得所有的 N≥N2 ,有 G(N)≤C2g(N) 。
令 C3=max{C1,C2},N3=max{N1,N2},h(N)=max{f,g} ,则对所有的 N≥N3 ,
F(N)≤C1f(N)≤C1h(N)≤C3h(N)
类似地,有
G(N)≤C2g(N)≤C2h(N)≤C3h(N)
因而
O(f)+O(g)=F(N)+G(N)≤C3h(N)+C3h(N)≤2C3h(N)=O(h)=O(max(f,g))
O(f)+O(g)=O(f+g) 证明
设 F(N)=O(f) 。根据符号 O 的定义,存在正常数 C1 和自然数 N1 ,使得对所有的 N≥N1 ,有 F(N)≤C1f(N) 。
类似地,设 G(N)=O(g) ,则存在正的常数 C2 和自然数 N2 ,使得所有的 N≥N2 ,有 G(N)≤C2g(N) 。
令 C3=max{C1,C2},N3=max{N1,N2},则对所有的 N≥N3 ,有
F(N)≤C1f(N)≤C3f(N)
G(N)≤C2g(N)≤C3g(N)
故有:
O(f)+O(g)=F(N)+G(N)≤C3f(N)+C3g(N)=C3(f(N)+g(N))=O(f+g)
O(f)O(g)=O(fg) 证明
设 F(N)=O(f) 。根据符号 O 的定义,存在正常数 C1 和自然数 N1 ,使得对所有的 N≥N1 ,有 F(N)≤C1f(N) 。
类似地,设 G(N)=O(g) ,则存在正的常数 C2 和自然数 N2 ,使得所有的 N≥N2 ,有 G(N)≤C2g(N) 。
令 C3=C1*C2, N3=max{N1,N2}, 则对所有的 N≥N3 ,有
F(N)≤C1f(N)
G(N)≤C2g(N)
故有:
O(f)*O(g)=F(N)*G(N)≤C1f(N)*C2g(N)=C3*f(N)*g(N)=O(f*g)
O(Cf(N))=O(f(N)) ,其中 C 是一个正的常数;
对O(f(N))设 F(N)=O(f(N)) 。根据符号 O 的定义,存在正常数 C0 和自然数 N0 ,使得对所有的 N≥N0 ,有F(N)≤C0f(N) 。
因而存在正常数C0/C和自然数N0,使得对所有 N≥N0 ,F(N)≤(C0/C)*Cf(N)
因而O(Cf(N))=O(f(N))
f=O(f) 证明
设 F(N)=O(f) 。根据符号 O 的定义,存在正常数 C1 和自然数 N1 ,使得对所有的 N≥N1 ,有 F(N)≤C1f(N) 。
故有:
O(f)=F(N)≤C1f(N)=f
根据符号 O 的定义,用它评估算法的复杂性,得到的只是当规模充分大时的一个上界。这个上界的阶越低,则评估的就越精确,结果就越有价值。
Ω :如果存在正的常数 C和自然数 N0 ,使得当 N≥N0 时有 f(N)≥Cg(N) ,则称函数 f(N) 当 N 充分大时下有界;且 g(N) 是它的一个下界,记为 f(N)=Ω(g(N)) 。这时还说 f(N) 的阶不低于 g(N)) 的阶。
同样要指出,用 Ω 评估算法的复杂性,得到的只是该复杂性的下界。这个下界的阶越高,则评估就越精确,结果就越有价值。它常常与符号 O 配合以证明某问题的一个特定算法是该问题的最优算法或该问题的某算法类中最优算法。
定义 f(N)=θ(g,(N)) 当且仅当 f(N)=O(g(N)) 且 f(N)=Ω(g(N)) 。这时,我们说 f(N)与g(N) 同阶。
最后,如果对于任意给定的 ε>0 ,都存在正整数 N0 ,使得当 N≥N0 时有 f(N)/g(N)<ε ,则称函数 f(N) 当 N 充分大时的阶比 g(N) 低,记为 f(N)=o(g(N)) 。