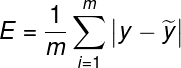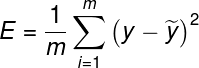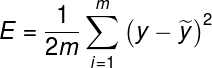「学习内容总结自 udacity 的深度学习课程,截图来自 udacity 的课件」
一. 建立简单线性回归
任务:本节练习提供的数据为各国男性人口的 BMI 与该国人口平均寿命。数据来自 Gapminder:https://www.gapminder.org
数据文件位于 "bmi_and_life_expectancy.csv" 中。其中 "Country" 列记录出生国家,"Life expectancy" 列记录该国平均寿命,"BMI" 列记录该国男性 BMI 数据。将使用 BMI 数据来预测平均寿命。
1.导入用到的库:
1)pandas:数据分析库,对数据处理和分析很有用处
2)scikit-learn:包含机器学习模型库,目前需要导入线性回归模型
import pandas as pd
from sklearn.linear_model import LinearRegression
2.加载数据集
需要用到 pandas 里的 read_csv() 函数导入 csv 文件
bmi_life_data = pd.read_csv("bmi_and_life_expectancy.csv")
3.建立模型并拟合数据
用 LinearRegression 类来创建线性回归模型,fit()函数拟合数据
bmi_life_model = LinearRegression()
bmi_life_model.fit([['BMI']],[['Life expectancy']])
4.预测模型
假设输入一个BMI的数据为:32.15678,预测平均寿命为多少。用predict()函数来预测
bmi_life_predict = bmi_life_model.predict(32.15678)
二.线性回归的注意事项
使用线性回归有一系列的隐含条件,并非所有条件都适用。需要注意下面两个事项:
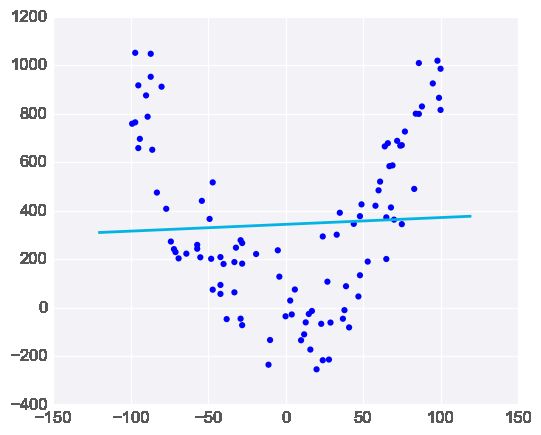
1.线性回归最适用于线性数据
线性回归会根据训练数据生成直线模型。如果训练数据包含非线性关系,就需要选择:调整数据(进行数据转换)、增加特征数量或改用其他模型。
2.线性回归容易受到异常值影响
线性回归的目标是求取对训练数据而言的 “最优拟合” 直线。如果数据集中存在不符合总体规律的异常值,最终结果将会存在不小偏差。
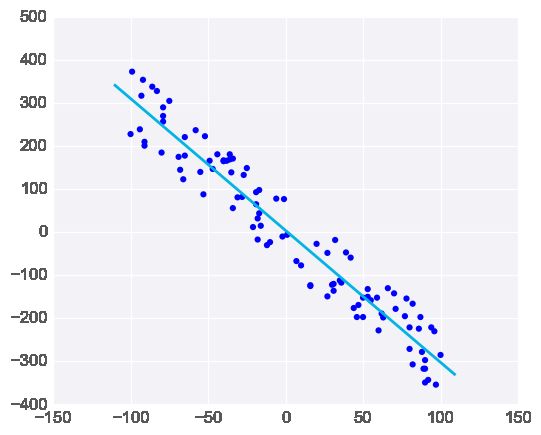
在第一个图表中,模型与数据相当拟合:
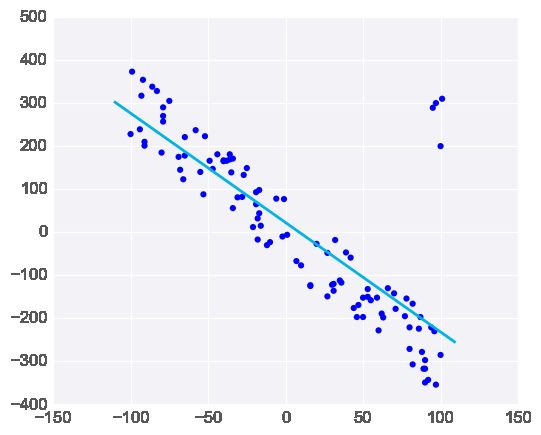
但若添加若干不符合规律的异常值,会明显改变模型的预测结果:
三.多元线性回归
我们在上面的任务练习中使用 BMI 来预测平均寿命。这里的 BMI 是预测变量,也称为自变量。预测变量被用来预测其他变量,而被预测的则称为因变量。
1)仅有单个预测变量时,线性回归可以用这个方程来描述:
y=mx+b
2)当有两个变量时,可以这样表示:
y=m1x1+m2x2+b
3)当有n个变量时,可以这样表示:
y=m1x1+m2x2+m3x3+...+mnxn+b
四. 评估线性模型的误差
-
平均绝对误差(Mean Absolute Error)
如下图所示,用一条直线拟合了坐标上的一些点,然后计算这些点到直线的竖直距离再求总和就是误差值。这种方法称为平均绝对误差。公式如下:
但这个方法有个缺点,即绝对值函数是不可微分的,会不利于使用梯度下降等方法。
在sklearn中的实现方法如下
from sklearn_metrics import mean_absolute_error
from sklearn_model import LinearRegression
classifier = LinearRegression()
classifier = fit(X,y) # 线性拟合模型
guesses = classifier.predict(X) #模型的预测值
error = mean_absolute_error(y,guesses) #平均绝对值误差
- 均方误差
为了避免平均绝对误差,引入更常见的指标-- 均方误差。均方误差是用一条直线拟合了坐标上的一些点,然后计算这些点到直线的竖直距离的平方再求总和,公式如下:
为了便于后面梯度下降法等的计算方便。常用这个公式: