阅读经典——《算法导论》03
矩阵乘法是种极其耗时的运算。
以C = A • B为例,其中A和B都是 n x n 的矩阵。根据矩阵乘法的定义,计算过程如下:
SQUARE-MATRIX-MULTIPLY(A, B)
n = A.rows
let C be a new nxn matrix
for i = 1 to n
for j = 1 to n
c[i][j] = 0
for k = 1 to n
c[i][j] += a[i][k] * b[k][j]
return C
由于存在三层循环,它的时间复杂度将达到O(n3)。
这是一个很可怕的数字。但是,凭着科学家们的智慧,这个数正在一步步下降。本文介绍经典的Strassen算法,该算法将时间复杂度降低到O(nlg7) ≈ O(n2.81)。别小看这个细微的改进,当n非常大时,该算法将比平凡算法节约大量时间。
分治法
Strassen算法基于分治的思想,因此我们首先考虑一个简单的分治策略。
每个 n x n 的矩阵都可以分割为四个 n/2 x n/2 的矩阵:
(式3-1)
因此可以将公式C = A • B改写为
(式3-2)
于是上式就等价于如下四个公式:
(式3-3)
C11 = A11 • B11 + A12 • B21
C12 = A11 • B12 + A12 • B22
C21 = A21 • B11 + A22 • B21
C22 = A21 • B12 + A22 • B22
每个公式需要计算两次矩阵乘法和一次矩阵加法,使用T(n)表示 n x n 矩阵乘法的时间复杂度,那么我们可以根据上面的分解得到一个递推公式。
T(n) = 8T(n/2) + Θ(n2)
其中,8T(n/2)表示8次矩阵乘法,而且相乘的矩阵规模降到了n/2。Θ(n2)表示4次矩阵加法的时间复杂度以及合并C矩阵的时间复杂度。
要想计算出T(n)并不复杂,可以采用画递归树的方式计算,或采用下一篇文章中讲的“主方法”直接计算。结果是
T(n) = Θ(n3)
可见,简单的分治策略并没有起到加速运算的效果。
Strassen算法
1969年,Volker Strassen发表文章提出一种渐进快于平凡算法的矩阵相乘算法,引起巨大轰动。在此之前,很少人敢设想一个算法能渐近快于平凡算法。矩阵乘法的渐近上界自此被改进了。
让我们回头观察前面使用分治策略的时候为什么无法提高速度。
因为分解后的问题包含了8次矩阵相乘和4次矩阵相加,就是这8次矩阵相乘导致了速度不能提升。于是我们想到能不能减少矩阵相乘的次数,取而代之的是矩阵相加的次数增加。Strassen正是利用了这一点。
现在,我们来看一下Strassen算法的原理。
仍然把每个矩阵分割为4份,然后创建如下10个中间矩阵:
S1 = B12 - B22
S2 = A11 + A12
S3 = A21 + A22
S4 = B21 - B11
S5 = A11 + A22
S6 = B11 + B22
S7 = A12 - A22
S8 = B21 + B22
S9 = A11 - A21
S10 = B11 + B12
接着,计算7次矩阵乘法:
P1 = A11 • S1
P2 = S2 • B22
P3 = S3 • B11
P4 = A22 • S4
P5 = S5 • S6
P6 = S7 • S8
P7 = S9 • S10
最后,根据这7个结果就可以计算出C矩阵:
C11 = P5 + P4 - P2 + P6
C12 = P1 + P2
C21 = P3 + P4
C22 = P5 + P1 - P3 - P7
是不是很神奇呢?话说我第一次看到这个算法的时候真的是惊呆了,10个S矩阵和7个P矩阵究竟是怎么凑出来的,简直不可思议。
我们可以把P矩阵和S矩阵展开,并带入最后的式子计算,会发现恰好是公式3中的四个式子。也就是说,Strassen为了计算公式3,绕了一大圈,用了更多的步骤,成功的把计算量变成了7个矩阵乘法和18个矩阵加法。虽然矩阵加法增加了好几倍,而矩阵乘法只减小了1个,但在数量级面前,18个加法仍然渐进快于1个乘法。这就是该算法的精妙之处。
同样地,我们可以写出Strassen算法的递推公式:
T(n) = 7T(n/2) + Θ(n2)
使用递归树或主方法可以计算出结果:
T(n) = Θ(nlg7) ≈ Θ(n2.81)
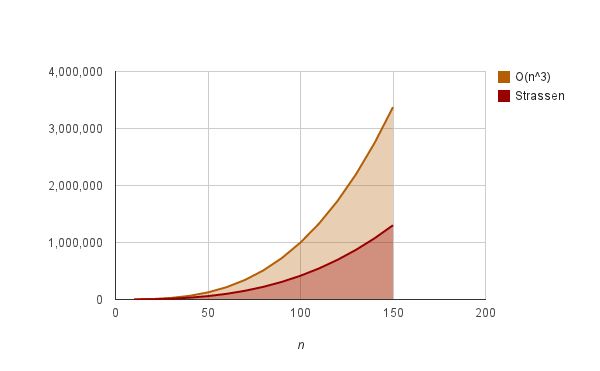
下图展示了平凡算法和Strassen算法的性能差异,n越大,Strassen算法节约的时间越多。
小技巧:如何计算n是否为2的幂
在矩阵分解的过程中,我遇到了这样一个问题:如何判断一个 n x n 的矩阵是否能恰好分解为4个大小相同的矩阵。它的本质是判断n是否为2的幂。
最先想到的方法是不断除以2,直到余数不为0时判断当前的被除数是否为1,是则为2的幂,否则不是2的幂。这相当于通过右移检查n的二进制形式是否为1000...0。
但这种方式有些繁琐,需要循环判断。为了提高效率,我发现有位高手用下面这行代码解决了这个问题:
n & (n - 1) == 0
没错,只需要一行代码,而且只做了一次加法运算和一次与运算,效率大大提高。其原理也很容易解释,把n和n-1的二进制形式写出来一看就明白了。假设n=0010 0000,那么n-1 = 0001 1111,相与得到
0010 0000
& 0001 1111
------------
0000 0000
恰好是0。只要把n中右边的任意一个0换成1,结果都不再是0。
还有一种类似的方法:
(n & -n) == n
本质和前面是一样的。据说后一种做法来自JDK,但我没有考证到。
参考资料
计算机算法:Strassen矩阵相乘算法 Stoimen
Gaussian Elimination is not Optimal Strassen