数组是最简单的数据结构,占据连续内存并且按顺序存储。
以下是与数组有关的算法题目。
(1)查询数组中重复数字
算法思路:(1)利用hash表,没有便放进去,有就返回(Java中HashMap存数字都是对象,判断数字是否唯一变为对象是否唯一,-128-127好说,其他不好说)。(2)借助基数排序思想,创建一个辅助数组(空间可能会很大)(3)i位置上j和j位置上元素互换,若j等于j位置上元素,说明重复(万一j的大小超出了矩数组大小则JJ)。(4)先排序,然后前后指针来实现,若A[i]==A[j] j++;若A[i]!=A[j] i = j;j++;
(2)二维数组的查找
算法思路:行、列有序,从小到大,则从右上角开始逼近,缩小搜索范围。
(3)把数组中的元素循环右移k位如12345678右移两位78123456
算法思路:3次翻转。把123456翻转65432178;把78翻转65432187;整体翻转78123456。
(4)字符数组中所有元素的排列
算法思路:利用递归,第一个字符一共有n种选择,剩下的变成一个n-1规模的递归问题。而第一个字符的n种选择,都是字符串里面的。因此可以使用第一个字符与剩下的位置上进行交换,得到n种情况,然后递归处理n-1的规模,只是处理完之后需要在换回来,变成原来字符的样子。
代码见:https://github.com/yuanfuqiang456/LeetCode/blob/master/src/Array/Permutation.java
(5)字符数组中所有元素的组合
算法思路:(1)通过二进制数字用01表示某个元素是否存在来实现,组合是没有顺序要求的(2)假设我们想在长度为n的字符串中求m个字符的组合。我们先从头扫描字符串的第一个字符。针对第一个字符,我们有两种选择:一是把这个字符放到组合中去,接下来我们需要在剩下的n-1个字符中选取m-1个字符;二是不把这个字符放到组合中去,接下来我们需要在剩下的n-1个字符中选择m个字符。这两种选择都很容易用递归实现。
代码见:https://github.com/yuanfuqiang456/LeetCode/blob/master/src/Array/Combine.java
(6)判断数组中的值是否连续
算法思路:数组中的0可以代替任何元素,如果没有0,则说明最大减去最小为数组大小;如果有0,则小于数组大小。例如:8 7 6 0 5 。
(7)寻找最小k个数
算法思路:方法一:先对这个序列从小到大排序,然后输出前面的最小的k个数;方法二:是维护容量为k的最大堆;方法三:快排思想。Partation,线性时间复杂度算法。
(8)和为定值的两个数
算法思路:1、二分(若无序,先排序后二分),时间复杂度总为O(N log N),空间复杂度为O(1);2、扫描一遍X-S[i] 映射到一个数组或构造hash表,时间复杂度为O(N),空间复杂度为O(N);3、两个指针两端扫描(若无序,先排序后扫描),时间复杂度最后为:有序O(N),无序O(Nlog N + N)=O(N log N),空间复杂度都为O(1)。
(9)和为定值的多个数
算法思路:如果取第n个数,那么问题就转化为“取前n-1个数使得它们的和为sum-n”,对应的代码语句就是sumOfkNumber(sum - n, n - 1);如果不取第n个数,那么问题就转化为“取前n-1个数使得他们的和为sum”,对应的代码语句为sumOfkNumber(sum, n - 1)。通过递归解法求出。
代码见https://github.com/yuanfuqiang456/LeetCode/blob/master/src/Array/KSum.java
(10)奇偶排序
输入一个整数数组,调整数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。要求时间复杂度为O(n)。
方法1: 借鉴partition的实现一,我们可以考虑维护两个指针,一个指针指向数组的第一个数字,我们称之为头指针,向右移动;一个指针指向最后一个数字,称之为尾指针,向左移动。这样,两个指针分别从数组的头部和尾部向数组的中间移动,如果第一个指针指向的数字是偶数而第二个指针指向的数字是奇数,我们就交换这两个数字。
方法2:我们也可以维护两个指针i和j,一个指针指向数组的第一个数的前一个位置,我们称之为后指针i,向右移动;一个指针指向数组第一个数,称之为前指针j,也向右移动,且前指针j先向右移动。如果前指针j指向的数字是奇数,则令i指针向右移动一位,然后交换i和j指针所各自指向的数字
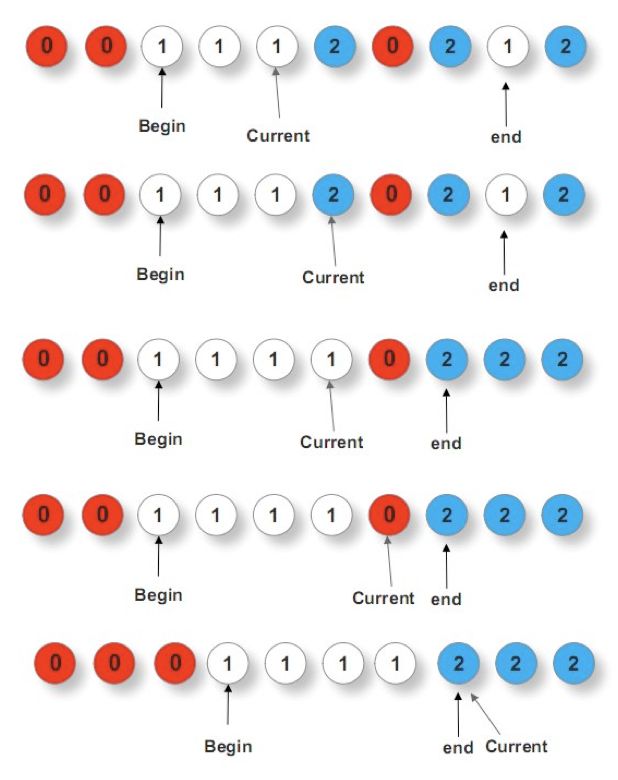
(11)荷兰国旗
现有n个红白蓝三种不同颜色的小球,乱序排列在一起,请通过两两交换任意两个球,使得从左至右,依次是一些红球、一些白球、一些蓝球。
算法思路:这个问题类似快排中partition过程,只是需要用到三个指针:一个前指针begin,一个中指针current,一个后指针end,current指针遍历整个数组序列,当
current指针所指元素为0时,与begin指针所指的元素交换,而后current++,begin++ ;
current指针所指元素为1时,不做任何交换(即球不动),而后current++ ;
current指针所指元素为2时,与end指针所指的元素交换,而后,current指针不动,end--
(12)完美洗牌算法
有个长度为2n的数组{a1,a2,a3,...,an,b1,b2,b3,...,bn},希望排序后{a1,b1,a2,b2,....,an,bn},请考虑有无时间复杂度o(n),空间复杂度0(1)的解法。
算法思路:方法1:蛮力B中的数步步前移;或者从中间开始两两交换;方法2: 前n个元素中,第i个元素去了第(2 * i)的位置。后n个元素,第i个元素去了第 (2 (i - n) ) - 1 = 2 i - (2 n + 1) = (2 i) % (2 * n + 1) 个位置。
(13)不使用除法进行数组运算
常见的算法面试题:两个数组a[N],b[N],其中A[N]的各个元素值已知,现给b[i]赋值,b[i]
= a[0]a[1]a[2]...*a[N-1]/a[i];要求解b[i],但是:
1.不准用除法运算
2.除了循环计数值,a[N],b[N]外,不准再用其他任何变量(包括局部变量,全局变量等)
3.满足时间复杂度O(n),空间复杂度O(1)。
算法思路:题目要求b[i] = a[0]a[1]a[2]...a[N-1]/a[i] ,相当于求:a[0]a[1]a[2]a[3]...a[i-1]a[i+1]..a[N-1],等价于除掉当前元素a[i],其他所有元素(a[i]左边部分,和a[i]右边部分)的积。
代码见https://github.com/yuanfuqiang456/LeetCode/blob/master/src/Array/CalculateWithoutMultiplication.java
(14)数组中唯一重复元素
1-1000放在含有1001个元素的数组中,只有唯一的一个元素值重复,其它均只出现一次。每个数组元素只能访问一次,设计一个算法,将它找出来;不用辅助存储空间,能否设计一个算法实现?
算法思路:做加法求和。
(15)找出唯一出现的数
一个数组里,数都是两两出现的,但是有三个数是唯一出现的,找出这三个数。
算法思路:相同数做异或运算结果为0,多次异或运算即可求出。
(16)找出反序的个数
给定一整型数组,若数组中某个下标值大的元素值小于某个下标值比它小的元素值,称这是一个反序。即:数组a[]; 对于i < j 且 a[i] > a[j],则称这是一个反序。给定一个数组,要求写一个函数,计算出这个数组里所有反序的个数。
算法思想:归并算法的思路。归并中需要调整的次数即反序的个数。
(17)两个数组元素求和,最小k个数
有两个序列A和B,A=(a1,a2,...,ak),B=(b1,b2,...,bk),A和B都按升序排列,对于1<=i,j<=k,求k个最小的(ai+bj),要求算法尽量高效。
算法思路:可借助最小堆来解决,由于a1+b1肯定是最小的和,首先把a1+b1的结果放大最小堆里,此时堆中只有一个元素,自然满足最小堆条件,然后开始出堆的操作,从堆里面取出根节点(也就是最小的值),假如此时堆顶元素为ai+bi,则需要像最小堆中压入a(i+1)+bj的和与ai+b(j+1)的和,当然,要保证下标不越界,如果下标越界了则忽略,另外要保证已经压入过堆中的组合(即使已经从堆中被取出了的)不再被压入堆中。不断地进行出堆、入堆的操作,重复k次,就得到了k个最小的组合值。
(18)螺旋矩阵
螺旋状打印矩阵
(19)一个整数数组,长度为n,将其分为m份,使各份的和相等,求m的最大值。
比如{3,2,4,3,6} 可以分成
{3,2,4,3,6} m=1;
{3,6}{2,4,3} m=2
{3,3}{2,4}{6} m=3
所以m的最大值为3。
算法思路:从1-N分别划分,找和为sum/N的数;
(20)输入一个正数n,输出所有和为n连续正数序列。
例如输入15,由于1+2+3+4+5=4+5+6=7+8=15,所以输出3个连续序列1-5、4-6和7-8。
算法思路:和为定值的N个数的多个K值的版本,且数字顺序要一致。若为奇数个,则中间数字为Sum/N;若为偶数个,则sum/n必定余1;通过这种方式,可以求出中间数字。
(21)找出数组中两个只出现一次的数字
题目:一个整型数组里除了两个数字之外,其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。
算法思路:异或操作。
(22)把数组排成最小的数
输入一个正整数数组,将它们连接起来排成一个数,输出能排出的所有数字中最小的一个。例如输入数组{32,321},则输出这两个能排成的最小数字32132。
算法思路:字典序排序,从前往后合并,如A,B比较AB与BA的大小,选最小的,然后逐步缩小数组长度。
(23)旋转数组的最小元素
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个排好序的数组的一个旋转,输出旋转数组的最小元素。例如数组{3, 4, 5, 1, 2}为{1, 2, 3, 4, 5}的一个旋转,该数组的最小值为1。
算法思路:从头到尾遍历数组一次,就能找出最小的元素,时间复杂度显然是O(N)。但这个思路没有利用输入数组的特性。可以2分查找,比较找到的元素与首位和末尾的元素,判断当前元素在哪个递增序列上。
(24)请把一个整形数组中重复的数字去掉
例如:1, 2, 0, 2, -1, 999, 3, 999, 88 ;处理后应该是:1, 2, 0, -1, 999, 3,88
算法思路:位图,hashtable.
(25)一个数组[1,2,3,4,6,8,9,4,8,11,18,19,100] 前半部分是是一个递增数组,后面一个还是递增数组,但整个数组不是递增数组,那么怎么最快的找出其中一个数?
算法思路:方法一:首先对前一半递增直接查找,找到即退出,后一半二分查找;方法二:找到零界点。分两个部分二分查找。临界点可2分查找,比较左右来判断。
(26)数组al[0,mid-1] 和al[mid,num-1],都分别有序。将其merge成有序数组al[0,num-1],要求空间复杂度O(1)。
算法思路:从中间开始两两互换,互换范围从2-4-6依次扩大。
(27)一个数组的值先从小到大递增后从大到小递减,找出最大的值
算法思路:二分查找,找到后和左右比较
(28)两个无序数组分别叫A和B,长度分别是m和n,求中位数,要求时间复杂度O(log(m+n)),空间复杂度O(1)
算法思路:首先先排序,分别求A和B的中位数,然后比较之,根据比较选择不同的数组区域继续进行筛选。假设两个数组为:Orda_1,Orda_2。先对比这个数组的中间数的大小,假设Orda_1的中间数为a_1,Orda_2的中间数为a_2,如果a_1 >= a_2,那么两个数组的中间数肯定在Orda_1数组前半段和Orda_2数组后半段中,接着再把Orda_1前半段和Orda_2后半段当做新的两个有序数组,重复前面的步骤,直至递归结束。
(29)约瑟夫环
n个数字(0,1,…,n-1)形成一个圆圈,从数字0开始,每次从这个圆圈中删除第m个数字(第一个为当前数字本身,第二个为当前数字的下一个数字)。当一个数字删除后,从被删除数字的下一个继续删除第m个数字。求出在这个圆圈中剩下的最后一个数字。
算法思路:每杀掉一个人,下一个人成为头,相当于把数组向前移动M位。若已知N-1个人时,胜利者的下标位置位f(N−1,M),则N个人的时候,就是往后移动M为,(因为有可能数组越界,超过的部分会被接到头上,所以还要模N),即f(N,M)=(f(N−1,M)+M)%n
递推公式:
f(N,M)=(f(N−1,M)+M)%N
f(N,M)表示,N个人报数,每报到M时杀掉那个人,最终胜利者的编号
f(N−1,M)表示,N-1个人报数,每报到M时杀掉那个人,最终胜利者的编号
代码见:https://github.com/yuanfuqiang456/LeetCode/blob/master/src/Array/JosephLink.java
(30)统计在从1到n的正数中1出现的次数
例如输入12,从1到12这些整数中包含1 的数字有1,10,11和12,1一共出现了5次。
算法思路:设定整数点(如1、10、100等等)作为位置点i(对应n的个位、十位、百位等等),分别对每个数位上有多少包含1的点进行分析。
根据设定的整数位置,对n进行分割,分为两部分,高位n/i,低位n%i
当i表示百位,且百位对应的数>=2,如n=31456,i=100,则a=314,b=56,此时百位为1的次数有a/10+1=32(最高两位0~31),每一次都包含100个连续的点,即共有(a/10+1)*100个点的百位为1
当i表示百位,且百位对应的数为1,如n=31156,i=100,则a=311,b=56,此时百位对应的就是1,则共有a/10(最高两位0-30)次是包含100个连续点,当最高两位为31(即a=311),本次只对应局部点00~56,共b+1次,所有点加起来共有(a/10*100)+(b+1),这些点百位对应为1
当i表示百位,且百位对应的数为0,如n=31056,i=100,则a=310,b=56,此时百位为1的次数有a/10=31(最高两位0~30)
综合以上三种情况,当百位对应0或>=2时,有(a+8)/10次包含所有100个点,还有当百位为1(a%10==1),需要增加局部点b+1
之所以补8,是因为当百位为0,则a/10==(a+8)/10,当百位>=2,补8会产生进位位,效果等同于(a/10+1)
(31)数量超过一半的元素
算法思路:排序,中间元素即是。
(32)两数组交换差最小
有两个序列a,b,大小都为n,序列元素的值是任意整数,无序。要求:通过交换a,b中的元素,使[序列a元素的和]与[序列b元素的和]之间的差最小。
例如:
var a=[100,99,98,1,2, 3];
var b=[1, 2, 3, 4,5,40]。
算法思路:看交换后两数组之和与所有数据和的1/2比较。是否更加接近