判断有向图中是否有环-课程安排(Leetcode207)

207. Course Schedule

There are a total of n courses you have to take, labeled from 0 to n-1.

Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]

Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?
Example 1:

Input: 2, [[1,0]]
Output: true
Explanation: There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
Example 2:

Input: 2, [[1,0],[0,1]]
Output: false
Explanation: There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should
also have finished course 1. So it is impossible.
Note:

1. The input prerequisites is a graph represented by a list of edges, not adjacency matrices. Read more about how a graph is represented.
2. You may assume that there are no duplicate edges in the input prerequisites.

题解：

有 n 个课程（0~n-1），课程之前存在依赖关系，比如想要学习课程 0，就需要先学习课程 1；输入 n 个课程的依赖关系，判断是否可以将这 n 个课程全部完成。
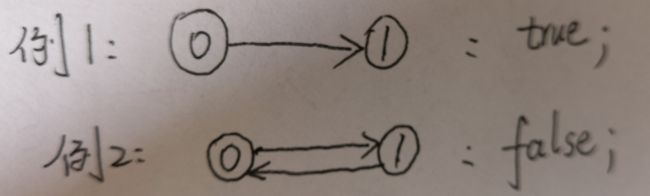
例：
输入：2, [[1,0]]；
2 表示两个课程， [[1,0]] 表示想要学习课程 1 需要先完成课程 0； 那我就先学 0 再学 1 就可以完成这 2 个课程了；
输出：true；
输入：2, [[1,0],[0,1]]
依然是两个课程，[[1,0],[0,1]] 表示想要学习课程 1 需要先完成课程 0；想要学习课程 0 需要先完成课程 1； 一脸懵逼发现死循环了，不可能将这两个课程全部完成；
输出：false；

分析：

这道题其实可以用有向图来实现；如图：

image.png

发现其实可以通过判断图中是否存在环来确认能否将课程全部完成；
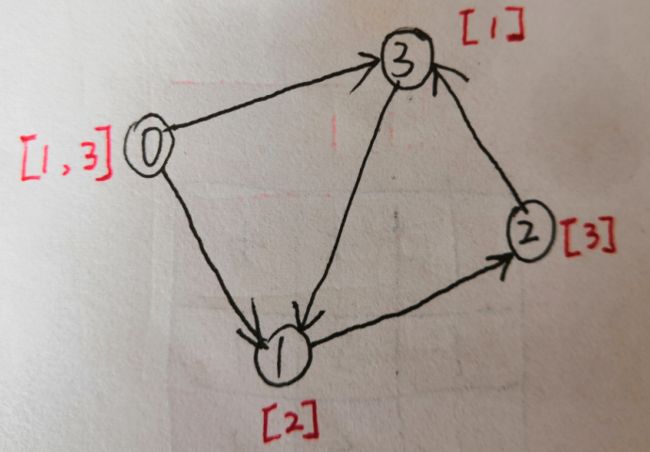
啥？你咋发现的，这才俩点啊？好吧，那我们给四个课程关系，搞波大的：

image.png

好的，emmm这图挺大了（笑）；分析下：
想要完成 0 ：需要完成 1，3；
想要完成 1 ：需要完成 2；
想要完成 2 ：需要完成 3；
想要完成 3 ：需要完成 1；
很明显，当我们要学习 1 的话，需要完成 2，学习 2 的话需要完成 3 ，学习 3 的话又要完成 1；这就死循环了，也就是图中的环；所以，只要构建的图中存在至少一个环的话，就一定无法完成所有课程；
那么重头戏来了，如何判断图中是否存在环呢？
我们用到了图的宽搜： https://www.jianshu.com/p/9828026169fc
对于图，我们可以删除入度为 0 的顶点，同时将从该点出发的相通的点入度减一；我们只要将图中所有入度为 0 的顶点全部删除，就可以判断图中是否有环了：如果图中所有顶点都能删除，说明所有的顶点最后入度都能减到 0 ，一定不存在环；反之，有环；而要实现这样一个过程，明显需要用到图的宽搜来解决；

image.png

遍历图中的顶点，对于每一个 未被访问过的顶点进行宽搜：
宽搜的过程中，将 入度为 1 的顶点存入队列中（因为入度为 1 说明该顶点只与当前队列头部的被宽搜的点相连，一旦删除队列头部的顶点，那么这个入度为 1 的点就是我们所需要的符合 入度为 0 的点；）；宽搜过程中，将该点相邻的顶点 入度减一；当前队列头顶点宽搜结束后，将 队列头删除，队列头变更为了新的入度为 0 的点，直到 相邻点中不存在减一后入度为 0 的点，宽搜结束；
重复该过程，直到所有顶点均已被访问过；
这时，再来判断，所有的顶点的 入度是否都为 0，都为 0 说明都被删除了，所以不存在环，反之，有环；

My Solution(C/C++)

#include 
#include 
#include 
#include 

using namespace std;

struct GraphNode {
    int label;
    vector neighbors;
    GraphNode(int x) : label(x) {}
};

class Solution {
public:
    bool canFinish(int numCourses, vector> &prerequisites) {
        vector Graph;
        vector visit;
        vector degree;  //顶点的入度
        for (int i = 0; i < numCourses; i++) {
            Graph.push_back(new GraphNode(i));
            visit.push_back(0);
            degree.push_back(0);
        }
        for (int i = 0; i < prerequisites.size(); i++) {
            GraphNode *begin = Graph[prerequisites[i].first];
            GraphNode *end = Graph[prerequisites[i].second];
            begin->neighbors.push_back(end);
            degree[end->label] += 1;
        }
        for (int i = 0; i < numCourses; i++) {
            //printf("Graph: %d degree: %d\n", Graph[i]->label, degree[i]);
            if (visit[Graph[i]->label] == 0 && degree[Graph[i]->label] == 0) {
                BFS_Graph(Graph[i], visit, degree);
            }
        }
        for (int i = 0; i < numCourses; i++) {
            //printf("Graph: %d degree: %d\n", Graph[i]->label, degree[i]);
            if (degree[Graph[i]->label] != 0) {
                return false;
            }
        }
        return true;
    }
private:
    void BFS_Graph(GraphNode *node, vector &visit, vector °ree) {  //从当前顶点宽搜，判断是否存在环；
        queue q;
        //printf("Node: %d\n", node->label);
        q.push(node);
        visit[node->label] = 1;
        while (!q.empty()) {
            for (int i = 0; i < q.front()->neighbors.size(); i++) {
                //printf("Graph: %d degree: %d\n", q.front()->neighbors[i]->label, degree[q.front()->neighbors[i]->label]);
                if (degree[q.front()->neighbors[i]->label] == 1) {
                    q.push(q.front()->neighbors[i]);
                }
                visit[q.front()->label] = 1;
                degree[q.front()->neighbors[i]->label] -= 1;
            }
            q.pop();
        }
    }
};

int main() {
    int numCourses = 4;
    //int numCourses = 10;
    vector> prerequisites;
    prerequisites.push_back(make_pair(0, 1));
    prerequisites.push_back(make_pair(0, 3));
    prerequisites.push_back(make_pair(1, 2));
    prerequisites.push_back(make_pair(2, 3));
    prerequisites.push_back(make_pair(3, 1));
    //prerequisites.push_back(make_pair(5, 8));
    //prerequisites.push_back(make_pair(3, 5));
    //prerequisites.push_back(make_pair(1, 9));
    //prerequisites.push_back(make_pair(4, 5));
    //prerequisites.push_back(make_pair(0, 2));
    //prerequisites.push_back(make_pair(7, 8));
    //prerequisites.push_back(make_pair(4, 9));
    Solution s;
    printf("%d\n", s.canFinish(numCourses, prerequisites));
    system("pause");
    return 0;
}

结果

0
请按任意键继续. . .