离散数学是跟整数有关的数学,也是计算机科学的基础,本章就着重于讲述如何将分数转化为整数的技巧
底和顶
我们使用以下标记
小于或等于的最大整数
大于或等于的最小整数
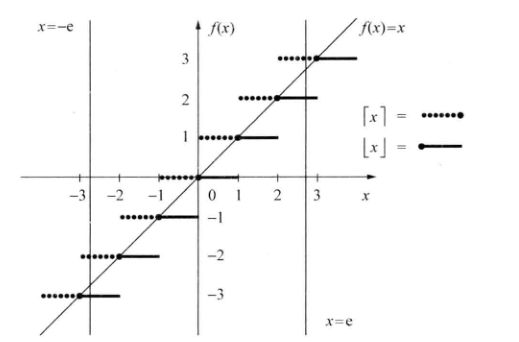
下面是一个函数的示意图
我们可以得出一个恒等式
这是因为当为整数时,,当不为整数时,
同样的很明显有
为了更直观的理解底和顶,可以通过以下不等式(其实就是上面不等式的变形,n表示一个整数)
同时像,可以将整数项挪入和挪出底或顶,但像则不可以
同样可以总结出以下几个不等式
我们把间的差称为的分数部分,同时称为的整数部分
对,,有
且,故有
等于或
等于或
底和顶的应用
任意一个整数写成二进制表示需要多少位?
经过简单的验证,我们可以通过或两种位数表示(这里默认的底显然是2)
而对于多个底或者顶的表达式,形如这样的内层是底或者顶外层多个底或者顶的表达式,可以把外层的底或者顶省略掉而不改变表达式的值
我们尝试证明以下命题
在证明其存在或不存在时,我们可以首先猜测一个可能的值,试图找一个反例去否定命题,一是因为否定更加容易,二是因为在寻找反例中,我们会有机会寻找到证明的方法。这个例子中,无论怎么尝试,是找不出反例来的。
如果我们借助微积分来证明,首先将分解为整数和分数部分,用牛顿二项式定理将其展开,但展开后过于复杂不好处理
我们换一种方式,先去掉原式左部分中外部的底和根号,然后去掉内层的底,最后将外层的符号还原回去最后得到右部分
首先设,根据性质1,有,
由于不等式三个值都是正的,将其平方,得
对这个不等式左边使用性质6,右边使用性质3,则有
再同时开方得,利用性质1,
即左式等于右式,命题得证
在以上证明中,并没有严重依赖平方根的性质,我们把这个命题推广:
设是任意一个具有如下性质且在实数区间连续的单调递增函数
只要都有定义,则有
下面是对顶的证明,底的证明类似
当,显然是成立的,否则,由于单调递增,非减,于是
如果,因为的连续性以及其必备的性质,必然存在一个整数,使得成立,但显然这样的数并不存在,于是命题得证
这个定理有如下一个应用特例
如果为整数且分母为正,则有
例如令,则,三次用10来除并抛弃个位数字,与用1000来除并抛弃余数,结果是一样的
重复下去即可得到左式结果
在了解上面对于数学问题水平的定义之上,我们研究一下以下等式等号成立的条件
我们在尝试几个数后发现,有时等号成立,有时不成立,以水平4的角度去寻找等号成立的条件会发现:
当时,等号左边为,右边则为,等号不成立
当时,等号成立
因此我们可以说等号成立的充要条件为:为整数或者不为整数
现在我们从区间的角度数一数其中的整数个数。我们知道开区间表示满足的所有取值,闭区间表示满足的所有取值,而半开半闭区间同理。事实上,两个同类型的半开半闭区间可以很方便的相加,但显然开区间和闭区间不能随便这么做。于是我们先从半开半闭区间研究。
当都为整数时,显然在区间内的整数有共个;区间内的整数有共个。
当为任意实数时,根据我们之前了解到的底和顶的性质,有
从而得出包含个整数,包含个整数,类似的包含个整数,包含个整数
这里规定一个习惯,对用顶来表示,对用底来表示,用表格来总结一下
| 区间 | 包含整数的个数 | 条件 |
|---|---|---|
下面我们看一个具体的例子来验证我们所总结的内容
计算1~1000中(包含两端)的整数个数,其满足,也就是一个数n能被它的立方根的底整除的条件
我们把个数设为,则有
注意到注释部分,之所以这么做是想要使得的取值范围变成一个半开半闭的区间,把单独列出来后,就可以做到这一点,之后使用上面表格中的性质就很方便了。
下面我们把1000这个具体的数字变成代数,同样的条件,我们来计算一下结果
我们设,也就是说,是小于或等于的立方根最大的整数,则根据上面我们计算的经验
后面的和式等于
故最后的答案为
这样就得出了一个一般性的答案
观察这个公式前两项近似于,而其余项可记做,在足够大的情况下,是可以忽略的,但在取一些不够大的值时,如果需要精确的数据,不可以随便忽略
下面我们讲一个新的概念:谱
一个实数的谱是整数组成的一个无限多重(元素可重复,数论里有讲)集合
例如的谱就是
谱有一个基本的性质,就是当时,,其证明如下:
假设,则存在一个正整数使得,即且,显然有少于个元素,而至少有个这样的元素
下面我们看一下谱一个有趣的性质,比如观察下面两个谱
观察到的第个元素恰好比的第个元素大,同时更惊人的是全体正整数是和的不相交并集,我们称这两个谱构成了正整数的一个划分
其证明思路就是对任意正整数,我们计算中有多少个元素是的,以及中有多少个元素是的,然后将两个值相加,如果等于,则命题得证
设是正数,中的元素个数是
在上面的推导中,有两处值得注意,首先有
均为整数
这一步将改为,根据性质3,可以将底去掉
同时我们限定求和而非,这是因为与区别的地方是有可能小于1,前者更加准确
下面我们套用这个公式,计算的结果
注意到在n为整数时必定不为整数,于是顶减1正好为底,于是可以化为
进一步化为
由于有恒等式
所以原式可以化为
也就是说只要我们证明
原式也就等于n了
我们设两个非整数,显然有,这两个数的整数部分的和显然是,分数部分的和显然就是1了,故命题得证
底和顶的递归式
含有底或顶的递归关系经常在计算机科学中出现,因为很多以分而治之为基础的算法,会把一个大小为的问题转化为的几分之一(取整)的多个小问题。例如给个记录排序的一种方法是把它们分为两个近乎相等的部分,一部分大小为,另一部分大小为,显然我们知道。在每一部分被分别排序后(切分过的部分自然也可以循环的切分为两部分),通过每一步做至多次比较,最后将这些记录合并成最后的排序,这样一来,我们设最终的比较次数最多为,则有
这里稍微解释一下为什么两个已排序的几乎等长(其实以最坏情况考虑,等长不等长结果是一样的)数组(为了叙述的习惯,叫数组比较顺口)需要至多次比较才能将两者合并为一个已排序的数组。我们惯用的方法是将两个数组两端(或者是最大或者是最小,这里举例用最小的)的元素进行比较,较小的放入新的存储结果的数组并改变这个数组的端点(角标向后移一位),较大的其数组端点保持不变,重复以上步骤直至两个数组中有一个没有元素,将另一个的数组中所有剩余的元素依次序放入新数组,结束整个步骤。显然每次比较会在新数组中填入一个元素,至多次比较后,一定会有一个数组元素为空,此时不再需要比较,直接将最后的元素填入新数组就结束了。
这个递归式的解在习题34中,我们提前把答案写出来
其封闭形式的计算如下:
我们设,则,显然当时,,这个区间有个整数,故和式可改写为
对可以化为,故原式可进一步化为
这个和式我们第二章有讲,这里直接给出答案
现在我们反过来计算
要知道的,所以我们有
注意这里式中的表示我们多计算了多少次,代表此时对应的值
所以最后化简得到
也就是说最终是一个比较次数为复杂度的算法
如果感兴趣的话,我们再来看一下如何证明这个答案就是我们需要的答案
绕了这么大一圈,我们回头看一下第一章的约瑟夫问题
此时我们可以更准确的将最基本的情况归纳为以下递归式
同时如果我们把条件变成每隔2人杀死一人,那么我们最终得到递归式
当 时
这个递归式有着分数、底和顶,想要化简不是一件容易的事,我们在下面给出一种更好的解决方案,同时附上其相应的java代码
我们规定每当循环中,一个人幸存了,就把他的号码替换为最大的号码加1,这样1号,2号跳过,于是变成了号,3号被杀,4号5号变成了,以此类推...和号变成号。最终是号被处死,比如当时,有下图
所以如果我们能算出标号为的人最初的号码,就可以获得我们想要的答案
当某时刻任意一个还活着的人的号码为时,如果,则他必定有一个以前的号码,则根据我们上文的规定,有或者,于是有,而这个人之前的号码分别可能为或,用一个式子来表示这两种情况可以通过
再把用表示,则上式可以写做,之后只需要不断把这个之前的号码以如上步骤循环迭代下去,直至这个号码,则这个号码就是最后活下去的人刚开始的编号
综上我们可以写出伪代码
虽然我们以上面的方式去设计算法,肯定是可以解出最后的答案的,但这个式子还是太复杂,我们尝试去简化这个算法
我们用来替换作为迭代的值,有,则我们根据上文中的迭代式从而写出的迭代式
此时我们将算法改写为:
在上一种算法中,从迭代减到小于等于,算法结束
而现在这种算法,从1迭代增到大于,算法结束
事实上,我们可以通过类似的推理获得一个结论:
当每隔个人就杀掉一人,幸存者可以使用以下方式计算
注意到这种算法的复杂度为
使用换底公式可以化为
显然除了之外,其余都是常数,所以复杂度是
下面我们看一下常见的解约瑟夫问题的算法,同时我们对其复杂度进行分析
这里我们用表示数到几的人被杀,表示一共多少人
先看一种最普通的解法:通过对环形单向链表的节点进行删除获得最后结果,其具体步骤如下:
- 如果链表节点数为1,或者m的值小于1,则直接返回
- 在环形单向链表中不断循环遍历每个节点,在此过程中,让节点报数
- 当报数从1到m时,删除报数为m的节点
- 删除节点后,注意要保持链表的环形状态
我们看一下具体的代码实现