第一篇
空时物理学
本篇不求助于完美的数学指导,先较快地(1.1)再稍慢地把读者引向Einstein几何动力学的主干及若干细节
第一章 几何动力学概要
1.1苹果的寓言
1666年的某一天, Newton来到了乡间,看见一只苹果掉下来,正如他的侄女告诉我的那样,这使他陷入了沉思:究竟是什么原因使每一个物体都沿着一条其延长线几乎通过地球中心的直线被拉下来呢? Voltaire (1738)
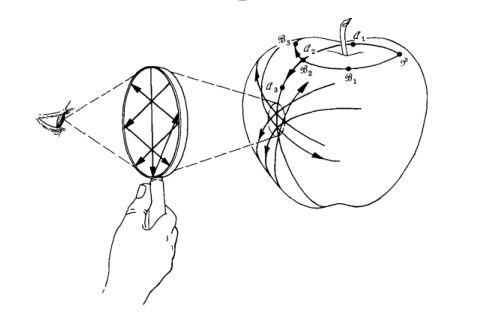
从前,有一个学生躺在花园里的一株苹果树下思索着Einstein和 Newton关于引力*的见解之间的差异。他为附近掉下的一个苹果所惊动。当他注视着个苹果时,他注意到一些蚂蚁开始沿着苹果表面爬行(1.1)。好奇心驱使他想研究蚂蚁所遵循的导航原理。他用放大镜仔细记下了一条足迹,又取出小刀,在苹果皮上这条足迹一侧一毫米处切了一刀,在它另一侧一毫米处也切了一刀。他削下苹果皮上这条小小的路径,并把它铺平在他的书面上。蚂蚁沿着这条路径的足迹像激光束那样笔直,要走过这一窄条从头至尾长十厘米的苹皮,蚂蚁再也找不出比这更简捷的这路了。沿着这条削下的苹果皮,从起点到终点,路径的任何曲折或甚至任何光滑的弯曲,都会增加它的长度
「多么美妙的一条短程线啊」。学生惊叹地说。
他的视线落在从同一点沿稍稍不同方向出发的两只蚂蚁上。它们的路径恰能使它们从两侧经过苹果顶端的下凹区域。每一只蚂蚁都认真的追随着它的短程线,并尽其所能,在苹果皮的窄条上直走。而且由于下凹处自身的弯曲
*在典力学中常源为「重力」此二法是等同的
图1.1
这里,以苹果表面的二维几何代表征广义相对论空时的 Riemann几何。以蚂蚁在苹果表面爬行的短程线足迹代表一自由粒子经过空时所循的世界线。在任何充分地局域化的空时区城内,正如在苹果的二维表面上,用放大镜看到的直足迹所表征的那样,几何学可以理想化为平直的(空时几何学的「局域 Lorentz性质」)。在一个更大的延展区域内,可以感
受到流形的弯曲(在实际的物理世界是四维空时,在苹果的情形是弯曲的二维几何学)
两条足迹和,起初从同一点散开,然后接近,交叉,再沿极为不同的方向分开。根据 Newton的理论,这个效应是由于吸引中心的超距引力作用所致,此处吸引中心由苹果柄表征。根据 Einstein的理论,一个粒子只能局域地,即从它所在处的空时几何,得到它的运动指令。这指令很简单:尽可能走一直最直的足迹(短程线)。物理学的简单正在于它可以是局域的。只是因为在大范圈内空时是弯曲的,足迹才相交。扼要地说,几何动力学就是几何对物质的效应(使起初分开的短程线相交)以及物质对几何的效应(质量集中引起的空时弯曲,此处以苹果柄对其附近苹果表面的效应表示)的双重故事。
两条足迹不仅交叉,还展示出很不同的方向。
「对于Einstein的重力的几何理论,人们可能祈求什么样的更为恰当的说明呢?」学生喃喃地说「蚂蚁似乎在苹果柄的吸引下移动。人们也许曾经相信过 Newton的超距作用力。然而,除了根据蚂蚁足迹沿线的局域几何外,蚂蚁是无从获得它的运动指令的。这确实是Einstein的概念,即全部物理学都是『局域作用』形成的。这和Newton物理学的『超距作用』观点多么不同啊现在,对这本书的含义我理解得更清楚了。」
他一边说,一边打开他的书朗读起来。「描写运动时,无须涉及远处物体。
仅当局域分析时,物理学才是简单的。局域地说,与任何世界线一样,一个
卫星(在围绕地球的空时中)所循的世界线也总是直线。忘掉所有关于『偏转』和『引力』的谈论吧。我在一艘宇宙飞船内,或者在飞船外边附近浮动时是否感受到任何『引力』呢?一点都没有。宇宙飞船是否感受到这样一个力呃?也没有。那么,为什么还要谈论它呢?应该认识到宇宙飞船和我都邀游在没有任何力的空时区域,应该承认经过该区域的运动已经是理想的直线了。吃饭玲响了,但学生仍旧坐在那里,独自思忖:「让我想一下,是否可以把Einstein的重力几何理论概括为三个观念:(1) 局域地说,短程线是直线;(2)在较宽广的空间和时间范围内,原先彼此分离的短程线开始以空时曲率所规定的速率互相靠近,而对于物质的这种几何效应就是今天我们用古老的『引力』一词所表达的意思。(3)反过来,物质又使几何弯曲。苹果上出现下凹,是由于果柄在那里。我想,我懂得怎样更为扼要地叙述整个故事了:空间作用于物质,决定了物质如何运动。而物质又反过来作用于空间,决定了空间怎样弯曲,换句话说, 「这里的物质」他拿住果柄,拾起苹果继续说,「使这里的空间弯曲,而使这里的空间弯曲就会迫使那里的空间也弯曲。」这时他注视着一只徘徊不去的蚂蚁,在离果柄一指宽处忙禄地沿其短程线爬行,并接着说:「因而,这里的物质影响着那里的物质,这就是Einstein对『引力』的解释。」
尔后,吃饭铃静下来,他带着书丶放大镜以及苹果离开了。
1.2带坐标和不带坐标的空时
现在。我想到:……引力加速度与落体的性质无关,可表述如下:在(空间广延很小的)引力场中,事物的行为与在无引力的空间中一样…..这种想法产生于1908年。为什么还要花费七年时才完成广羲相对论呢?主要原因是人们难以摆脱坐标必须具有直接度规意义的观念 Einstein (1949)
在这个陌生的领域中,初次接触「弯曲空时」概念时,最令人苦恼的是担心每一种简单的测量方法都会失去功效。试设想,在波涛汹涌的海面上,有人站在颠簸的划艇中,手中拿着一根米尺,面临着测量既庞大又刻蚀成奇形怪状的冰山形状的任务。如果要测量划艇本身的形状,办法很简单。把划艇拉上海岸,翻过来,在它表面各关键点轻轻地钉上一些平头钉。记下测出的各平头钉之间的距离,即可显示其表面形状。任意地增加平头钉的数目,即可使测量精度任意地提高。而想在高耸的冰山上钉上一些作为标志的爬山钉:就需要更大的勇气。但是,即使具有人世间的全部勇气。又怎样把钉子钉入空时以标志
图1.2
在装满干草的谷仓中稻草的交叉,对于充满空时的世界线而言,是一种象征。这些世界线,利用它们的交叉和弯曲,完全不需要坐标系和坐标,就可以唯一地标明一些事件。图中,从左到右用黑点标出的典型事件是:光子的吸收;光子的再发射;粒子和粒子的碰撞;光子和粒子的碰撞;光子和粒子的另一次碰撞;爆竹的爆炸;以及外来粒子与该爆竹碎片的碰撞。
一个点呢?幸而,正如Einstein首先强调指出的那样,自然界本身提供了定域空时中一点的方法。即用某处发生的事来表示该点的特征!给空时中的点定名为
「事件」。事件所在的位置是清晰分明的(图1.2),正如在充满干草的谷仓,两根稻草彼此交叉的位置一样。指出事件标志了某某光子与某某粒子的一次碰撞,就足以识别了。该光子和该粒子的世界都根植于过去,并延伸到未来。它们与附近的世界线联成一幅富丽的网。而附近的这些世界线又以成千上百种方式联系着更远的世界线。那么,人们怎样指出一个事件的位置呢?首先指出哪些世界线参与了这个事件。其次,跟踪这些世界线中的每一根,为它们所过到的另外一些事件命名。这些事件可以挑出更远的世界线。最后,整个装草的谷仓都被编目。每一个事件均被命名。正像市民能选出到圣会姆斯街和
图1.3
上图:利用坐标系,规定各事件的「电话号码」。所谓坐标系是「平滑」的,意既几乎在同一地点的各事件应具有几乎同样的坐标。
下图:利用不同坐标系:同样可把同一组事件编成很好的次序。这里,特别挑出两个邻近的事件,「」事件,其坐标为
「」事件,其坐标为
。事件「」和「 」通过间隔「矢量」相联。(在弯曲空时中,矢量的精确定义要求取两点的间隔为;无限小的数学极限[间隔 的N重缩并]。并且,在所得的局域平坦空间中,将间隔乘以因子N[;切向空间;切向矢量]。这里,我们摈弃了描选事物的固有方法,摈弃了完全的精确度,因而「矢量」这个词加上了引号。)在每一种坐标系中间隔矢量用「分量」(各坐标值之差)表征:
关于事件,坐标和矢量的详述,参看框1.1
框1.1
事件用一个大写草体拉丁字母表示,如:有时还加用下角标。
事件的坐标表为,或或更简单的表为 或其中希腊文指标理解为可取0,1,2,3中的任何值。
时间坐标(设已选定四个坐标之一担任此角色)。
空间坐标为有时表为拉丁文指标可理解为可取值1,2,3中的任何值。
简化符号:人们不久就会厌倦已明显的写出坐标的函数依赖关系;因此,对于事件的坐标,采用简化符号,对于事件的空间坐标采用简化符号,人们甚至一开始就想用来表示事件本身,但必须提醒自己:的值不仅取决于的选择,还取决于坐标的任意选择。
其他坐标:对同一事件的其他坐标可表为或,或,或例:图1.3中和指的是同一事件,用横线,撇,帽号把某一个坐标系与其他坐标系区别开来;把他们加在指标上,而不是x上,是为了简化后者的符号。
变换:从一个坐标系到另一个坐标系的变换可用四个函数来完成
间隔矢量*:从一个事件到邻近事件的间隔矢量(小箭头)可简要的表为也可以用的坐标值之(称为矢量的分量)表示,。
分量的变换:因为,所以从一个坐标系到另一个坐标系,矢量分量的变换变换方程的偏微商来完成
Einstein求和惯例:在此采用Einstein求和惯例,即在乘积中任何重复的指标自动求和
*矢量的这一定义只适用于平直空时。在弯曲空时中改进定义(切向矢量)现在还写不出来(见第九章),但当两个点充分接近时,即使在弯曲几何找那个也可以把平直几何的概念作为很好的近似来使用。
仅当所考虑的空时区域是平直的,且坐标是Lorentz坐标时,这些公式才是精密准确的。否则,它们是近似的,不过当点的间距和矢量长度任意变小时,它们变得任意精确。
皮卡迪利街的叉路口的路线一样,人们也一定能够找出到达给定交点的方法
这里无需数字。无需坐标系。无需坐标。在日本,大部分街这道有路名,大部分房子没有号码,这说明人们有能力识别,而无需坐标。作为识别在两条世界线交叉点处发生事件的方法,可以不管这两世界线的名称。正像人们可用年长居民的姓名命名一幢日本厉子一样对于空时中的特定事件,人们可以并常常加上任意的名称,如框1.1所示,然而,使用坐标是方便的。要不然,人们怎么能够轻易地从既大又厚、随意编排的事件目录中看出:沿着某一条世界线,首先会遇到事件T,其次遇到事件B,再次是事件M,然后是事件A—而不是这几个同样事件的某种置换了的次序呢?
为了使各种事件井然有序,应引入坐标!(见图1.3)在空时中每一个事件的坐标是四个标志数,在一张纸片上的事件只有二个标志数。事件T的坐标是
用坐标命名事件时,应要求平滑性,而放弃测量的各种想法。一个事件的四个数没有什么含义。只不过是某类精心制作的电话号码。比较两个事件的「电话」号码,可以确定它们是否邻近。但是,不要指望从电话号码的差别中得出它们相距多少来!无法禁止互相竞争的电话公司为用户服务,也无法禁止用不同的坐标系为事件编目(图1.3)。框1.1说明了一个坐标系和另一个坐标系之间的关系并列出了用来表示坐标及其间变换的符号。
选择两个事件,由于它们在一平滑坐标系中的坐标值相近,而知其为近邻事件。从一事件到另一事件画一小箭头。这样的箭头叫做矢量(在平直空时或弯曲空时中趋于零的长度,这是一个十分明确的概念;但对于弯曲空时中的有限长度,必须在新的名称「切向矢量」下予以改进并精确化,参看第九章)
这一矢量,像事件一样,可以命名。但无论命名J、C或K,它只是一个单值的十分明确的几何对象。使用名称固然有方便之处但即使不用名称,矢量仍然存在。
正如四个坐标
对于事件「T」是特别有用的名称一样(它可用来辨别哪些其它事件是邻近的),因此四个「分量」
对于从
引到
的矢量J也是方便的名称。框1.1讨论了一个矢量的分量如何起作用。
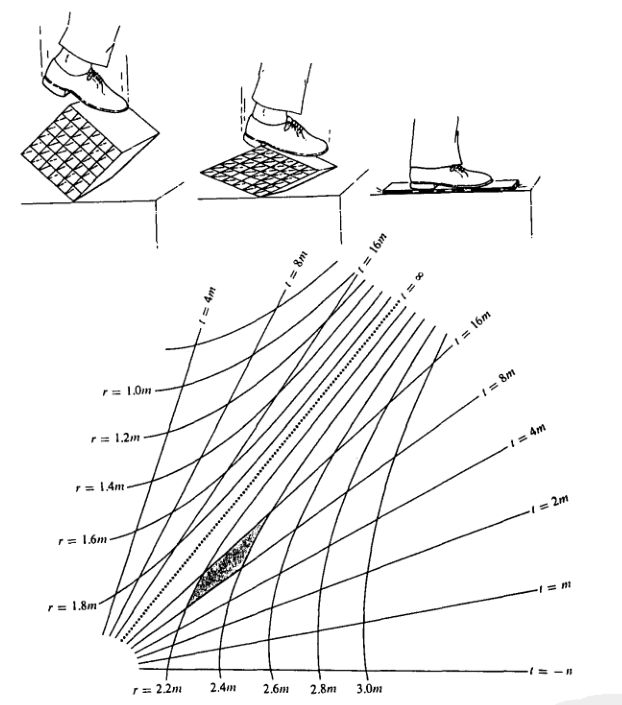
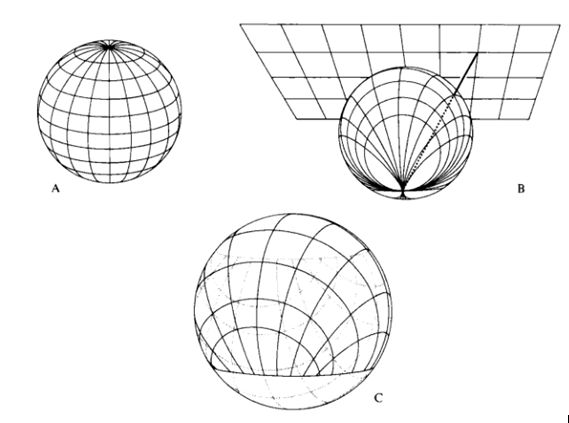
对此,有许多做法,其中坐标系可能是不完全的。图1.4说明了一个坐标奇点。作为另一个坐标奇点的例子,试沿地球仪表面浏览到北极,注意到许多子午线在这里会令(「鸡蛋框的小方格塌缩到容积为零」)。人们是否能做得更好呢?人们是否能找到一种简单的坐标系覆盖地球仪而无奇点呢?有一条定理断定:不能!要求无奇点地覆盖二维球面的「布片」的最小数目2(图1.5)。这一情况再次强调,点和事件是第一性的,而坐标只不过是一种记录手段而已。
图1.2和图1.3仅画出少数几根世界线和事件。更详细的图将使世界线、光线以及它们的相交点显得十分迷乱。从这样的图象出发,可以想象理想化的极限情形,即光线和无限小试验粒子的世界线无限密集。根据这一理想化的物理极限,连续四维「流形」(具有一定的平滑性质的四维空间)的数学概念就有了一一对应;并且,在此极限下,可运用连读、可微的(即平滑的)坐标系。因此,数学提供了推演物理学的工具。简单地倒着数可以揭示流形的维数。在n维流形中取一点,其邻域是n维球(即表面维n-1维的球形内部)。选择此球使其边界是一平滑流形。这一流形的维数是(n-1)。在此(n-1)维流形中挑选一点,其邻域是一个(n-1)维球。选择此球使得……等等。按这种方法最后会得到二维流形,但却并不知这是否就是二维的流形(二维球)。在此二维流形中挑选一点。其邻域是二维球(「图盘」)。选择此图盘使其边界是平滑的流形(图)。在此流形中挑选一点。它的邻域应是一维球,但并不知这是否就是一维的(「线段」)。这一对象的边界是两个点。这种情况表明伸在两点之间的流形是一维的。因此前一个流形是二维的,等等。原始流形的维数等于在此方法中所使用的点的数目。对于空时来说,维数是4。如果根据高能(相应的 de broglie波长为厘米)量子电动力学的预言和观测的符令一致来判断,那么,维数的这种数学论证对于日常的距离尺度、原子距离(厘米)、核线度(厘米)以及甚至更小几个量极的长度,都有完善的意义。此外,经典广义相对论把空时流形看作是一种决定论的
图1.4
单纯的坐标奇点是如何发生的。上图:当「鸡蛋框的小方格」压扁到体积零时,坐标系变成奇异的。下图:显示 Schwarzschild坐标r,t中这种奇点的一个例子,它常用来描述黑洞周围的几何(第三十一章)。简单起见,删去了角坐标,中。奇点本身可用两种方法表示。其一,虚线上彼此完全不同的全部点都用同一对(r,t)值,即r=2m,t=∞来表示。此坐标无法区分这些点。其二,「鸡蛋框的小方格」(图中,小方格之一用灰色表示)在虚线上坍缩到容积为零。总之,虚线上的几何并不陌生,全部奇点都取决于坐标系(「拙劣的电话号码系统」)。坐标t沿虚线取无限大值的偶然情形,不应引起混乱。
如果定义
(t/2m)= tan(/2m)
用新坐标来代替t,那么,这类无限大就不会发生。当=∞时,新坐标。坐标r,仍无法区分虚线上的点·它们仍然给出「鸡蛋框的小方格」沿虚线坍缩到容积为零。
图1.5
在二维球面上通常坐标的奇点可用两个交迭的坐标布片覆盖球面来滑除。A.球极坐标,奇
异性在南北极,不连续性在国际日界线。B. Euclid二维平面与球面在北极相切,通过引向南极的直线,平面上的 Euclid坐标投影于球面,坐标奇点在南极C.采用两个交迭坐标布片的二维球面的覆盖层。按照B那样做法,一片无奇点地覆盖北半球以及直到回归线的南部热带区,另一片(灰线)也可以无奇点地覆盖整个热带区以及南半球。
结构,这种结构直到任意小的距离都定义得很完善。与之不同,量子广义相对
论或「量子几何动力学」预言,在Planck长度
$L ^ { * } = \left( \hbar G / c ^ { 3 }\right) ^ { 1 / 2 }$
=
(1·1)
量极的距离上几何形状有激烈的起伏。没有人找到摆脱这一预言的任何方法。在尙可估计的邻域内,这些起伏赋于空间在小距离上一种『多连通的」或「类泡沫的」特性。在 Planck距离的尺度上,这总平滑性的丧失甚至完全剥夺了任何意义下的维数概念本身。这一论点的进一步研究,引导到 Einstein理论的前沿(第四十四章)。
如果空时在小距离上离开连续流形的数学模型很远,那么,在较大的距离上,数学的理想化和物理的现实之间不是也会有很大的差距吗?光线的无限密集以及无限小试验粒子的世界线的无限密集定义了流形的全部点;它们确实超出了实际的真实。从来没有人见到过在类时世界线上运动的粒子(有限静止质量)比电子要轻。电子的集令,即使其电荷密度为零(e+和e-的世界线数相等),仍具有质量密度。这一密度将使所研究的真实流形弯曲。无限细致的研究意味着密度不受限制,几何的干扰不受限制。
然而,正像在电动力学或气体动力学中那样,在刚才所述意义下,无限细致可研究性的要求,在广义相对论中也是不适当的。电动力学讨论空间每一点以及每一时刻的电磁场强度。为了测量那些场值,可以设想把无限小试验粒子按随意密集程度分散于各处。然而,根本毋需这些试验粒子来得出该处的真实场。不论有无无限小的试验粒子,场处处都有确定值,并必将连续进行其确定的动力学演化。空间的几何学与之类似。
最后,在经典物理范圈内研究空时的时候,应承认(1)「无限小试验粒子的观念,(2)可区别事件的总体可以理想化为四维连续流形。仅在本书的结尾在按某种方式论述和分析空时的时候,再给出量子原理所引起的某些限制的概貌。
1.3失 重
「重力是一个巨大的迷。丢下一块石头,看着它下落,听见它落地。可谁也不明白是什么道理。」多么令人迷惑的谈吐!下落难道还是个谜?石块不下落还能怎么样呢?下落是正常的。反常的倒是有物体挡在石块下落的路上。如果有人希望揭开「迷」底,他无需跟踪石块下落的轨迹,而应当去观察撞击,并且硏究是什么力把石块从它的自然的「世界线」(即它通过空时的自然轨迹)推开了。这将导致一个有趣的固体物理学问题,但已不是此处所谈的题目。此处涉及的是下落。自由下落是失重的同义语:没有任何力把物体推离它通过空时的正常轨迹。为了体验失重,可以乘坐自由下落的升降机,或者乘坐笔直落向地球的宇宙飞船。或者更愉快地乘坐沿国轨道运行的平糖地落向地球的宇宙飞船。在这些情况下,人们都是循着一条通过空时的自然轨迹运动。
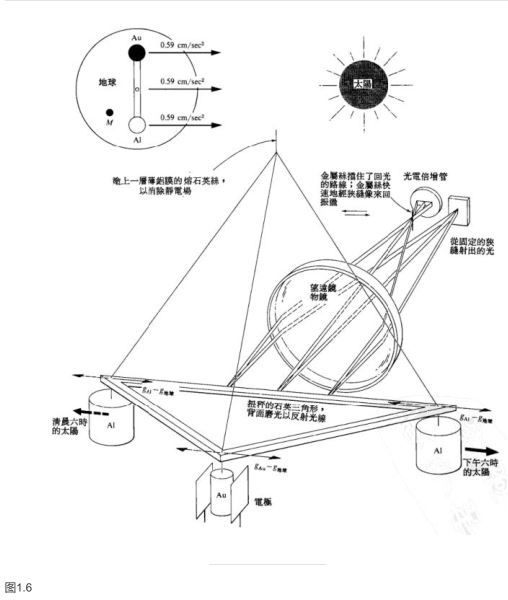
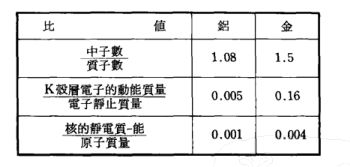
旅行者具有一种化学租成,宇宙飞船具有另一种化学租成,但是它们在起旅行,旅行者在其运动之冢中失重,根据Roll,Krotkov和 Dicke在1964年所作的实验,这一实验在全部物理学中是最重要的示零实验之一,参看图1.6,由诸如铝和金之类不同核成分组成成的物体,其下落加速度之间的相符优于10^{11}分之一。各个分子也与宏观物下落的步调一致[ Estermann, Simpson,和 Stern(1938)];各个中子[ Dabbs, Harvey,Paya,和Horstmann(1965)],各个电子[ Witteborn和 Fairbank(1967)],以及各个μ子[ Beall(1970)]也
图1.6
Roll-Krotkow- Dicke实验的原理。此实验表明金和铝引力加速度的一致达到或优于分之一(普林斯顿,1964)·如图左上角所示,质量相等的金和铝悬挂在一根支撑棒的两端,棒则在其中点受到支撑。若两物体以相同加速度落向太阳,则棒不旋转。若金得到较大的加速度,则在固定于地球的参考系中看来,棒的金端将向太阳方向旋转。十二小时后,因太阳处在另一侧,故从反向拉棒。由于这个交变的力矩具有精确的24小时周期,因而很容易从背景噪声中证认出来。令人不快的是,近处任何相当大的质量,如M处的实验者,都将产生一个力矩·它会淹没所寻找的效应。因此,实际的安排如图中主体部分所示。一金制重物和二铝制重物质于水平等边三角形的三个顶点,三角形边长6厘米,(三重对称轴,对于引力场中一切最简单的非均匀性都无响应)。又,观测者在远处进行一切操作,以消除自身的引力效应*。为了在不影响平衡的情况下探测到扭秤小至弧度的转动,Roll, Krotkov和 Dicke从石英三角形的光学平的背面反射一束非常弱的光线。源狭缝的像落在大小与狭缝像相近的金属丝上。越过金属丝的光线落在光电倍增管上。一个单独的振荡电路以3000赫的频率推动金属丝来回扫过该像。当像恰好处于中间时。光的强度中只出现振荡频率的偶次谐波。而当像稍稍偏向一边时,基频将要在光的强度中出现。这时光电倍增管的电输出将包含3000赫的成份。自动地测定还个成份的量值和符号,同样自动地在如图所示的电极上施加一个与之成比例的直流电压。它使扭秤恢复到初始位置。自动记录使扭秤恢复其初始位置的直流电压值,以此量度作用于摆的力矩。
对多日的力矩作 Fourier分析。以24小时为周期的 Fourier分量的量值表明比值=。因此,尽管金和铝有如下表所列的重要不同·却是以同样加速度下落的。
本实验的理论含意将在第十六章和第三十八章详加讨论。
莫斯科大学的 Braginsky和 Panov(1971)会作过一个实验,其原理与Roll- Krotkov- Dicke的相同,而实验装置有所改进。比较了白金和铝(而不是金和铝)的加速度,他们宣称
*其他干扰必防止,也已轻防止了·(1)扭秤边上厘米大小的一点点铁,就会在地磁场中产生出比所测力矩大百倍的力矩。 (2)只要物体两侧的温度差超过K,则两侧的不同幅射压就会产生大得不可容许的干扰。(3)从物体一侧散发的气体就像火箭一样推动此物体。当气体散发的速度大到克/日时,计算表明力可达,足以影响测量结果。 (4)旋转是相对于支承整个装置的墩子测出的。为了保证墩子本身不转动,把它固定在岩床上。(5)应消除静电力,不然它们会干扰平衡。
都是这样。不仅如此,这些物体中没有哪一个必须观看远处的空间才能知道自己应如何运动。注视一个宇宙飞船的内部,注视偶然地或按计划自由放置在飞船内部的钥匙、硬币、核桃或豌豆。它们因飞船舱壁而与船外边的世界隔开但是每个物体相对飞船而言保持静止,或者在室内作匀速直线运动。这就是经验的大声告戒。不要再讲到加速度!「所有物体都以同样加速度下落」这一教义是荒谬的。归根到底,那些加速度应归咎于谁呢?加速度来自允许一个地面观察者在场。地面观测者由于脚下地面的推举而偏离了自己的自然世界线。由于安排中的这一弊病,他便需对所有这些加速度负责。把他放入空间,并用皮带把火箭捆在他的腿上。毫无差别*!他仍需对他所见到的负责。他再一次注意到「一切物体都以相同的加速度下落」。由喷汽发动机推动的观测者和站在地面的观测者看来,物理学是同样复杂的。取消着两类观测者,代之以乘坐自由运动的宇宙飞船旅行,就使得物理学看起来简单明了。这时没有什么能比他所看见的更为自然了:每一个自由物体都作匀速直线运动。这就是研究物理学的方法!在
*「毫无差别」说明了 Einstein(1911)关于「引力场」和加速度之局域等效这一原理的全部内容。「如果假设参考系K和K’在物理上完全等效,即假设可以同样认为K系也处在无引力场的空间之中,物理上完全等效的假设,使我们不能再谈参考系的绝对加速度,正如通常的相对论禁止谈论一个系统的绝对速度一样,这使得引力场中所有物体应同样下落是理所当然的。
图1.7
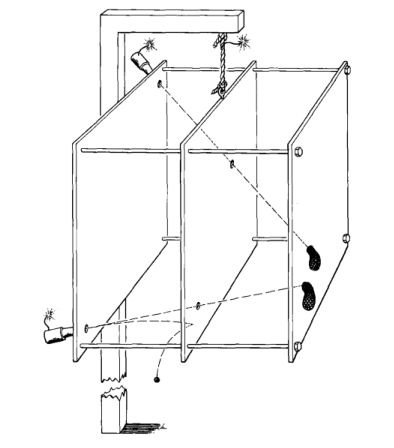
用失重检验局域惯性参考系(「Lorentz参考系」)当框架无旋转地自由下落(「通过空时的正常世界线」)时,每个弹簧炮都能成功地把它的弹丸,一颗钢球,经留西特(lucite)板上排成直线的几个洞口,射入袋之中。发炮时,若框架如图所示那样悬挂着(「框架被绳子从其通过空时的正常世界线拉开」),则发射将失败(在图下部弹道弯曲并弹跳)。普林斯幁的 Harold Waage会用约一米见方的留西特板作成一个这样的惯性参考系模型。其中,用继电器代替象征时间延迟的「熔断器」。当框架(1)旋转(2)加速(3)上两者的任意组合,穿透都会失败。很难引述任何其它能更清楚地阐明「局域 Lorentz参考系」的含义而又易于实现的装置了。
一个非常特殊的坐标系中从事工作;这就是一个失重的坐标系,即局域惯性参考系。或者计算一下物体在这种参考系中看起来会如何运动,或者一如果观测者被迫处于地面参考系时——利用一个运动得很快的粒子,并且路径的长度很有限,则理想的自由下落的参考系与实际的地面参考系偏离准直的总量在实验的尺度上可以忽略。[例如给定1500米长的直线加速器,以及一个一京电子伏的电子,则飞行时间≈(1.5×10^5厘米)/(3×10^{10}厘米/秒)=0.5×10^{-5}秒;在这段时间内自由下落的距离≈1/2gt^2=(490米/秒^2)(0.5×10^{-5}秒)^2≈10^{-8}厘米。]
在局域惯性参考系中分析物理学时,或者沿着一小条苹果皮追踪妈蚁时,放弃各个远离的参考系就赢得了简明性。只有局域地观察时,物理学才是简单的!这就是 Einstein的至关重大的吿诚。
Newton与此不同地说过:「绝对空间,按照其自身的性质,与任何外界事物无关,永远保持同一和静止」。但是,人们应如何赋于 Newton的绝对空间以含义,如何找出它的基石,并标志出它的直线呢?在实际的引力世界中,从来没有一个粒子沿着一条Newton的理想几何学超越于观测之外。「一颗彗星经过太阳旁边时偏离了理想的直线」。不对。不存在一条可以标志出该直线的路面。所谓「理想的直线」只是一个神话。它从来没有存在过,将来也不会存在。
(对于 Newton来说)为了得到发展理论所不可缺少的,独立而绝对的空间概念,曾经经历了一番激烈的斗争…… Newton的决定,在当时的科学状况下,是唯一可能的决定,而且特别也是唯一有效的决定。但是这问题以后的发展,却循着一条当时谁也无法预见到的曲折道路前进,它表明 Leibniz 和Huygens的那种直觉上有根据的,但以不适当的论据来支持的抵制,实际上是正常的。……尔后,人们仍需要付出同样艰巨的努力来战胜这个[绝对空间的]概念」[A. Einstein (1954)].
按照 Einstein的意见,直接、简单而有意义的是每一个局域惯性参考系中几何学的特征。在局域惯性系中每一个粒子都作匀速直线运动。定义局域惯性系使得第一批少数粒子具有这种简明性(图1.7)。则在这样定义的参考系中,观测到每一个其它的自由粒子也都作匀速直线运动。碰撞和蜕变过程遵从狭义相对论的动量和能量守恒定律。为基本粒子物理学中成千上万次观测所证实的所有这些奇迹的出现,证明了世界这部机器的内在作用。这些启示很容易概括如下:(1)物理学始终而且处处是局域Lorentz的,即局域而言特殊相对论的规律适用;(2)这种简明性最淸楚地表现在局域 Lorentz参照中(「惯性参考系」;图1.7);(3)为了检验局域 Lorentz参考系,可以检验失重!