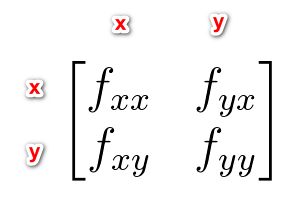一、说明
本博客讲述内容根据MIT线性代数第二十八课归纳而成。
MIT线性代数链接:http://open.163.com/newview/movie/courseintro?newurl=%2Fspecial%2Fopencourse%2Fdaishu.html
二、主要讲述问题
1-如何判断一个矩阵是正定矩阵
2-正定矩阵的最小值
3-正定矩阵的几何解释
三、如何判断一个矩阵是正定矩阵
1-正定矩阵
一个矩阵是正定矩阵,那么必须要满足以下的关系
(1)它必须是一个nXn的方阵(我们用符号A来表示)
(2)对于任意的一个向量x(不是每一个元素都是0), 都必须满足这样的一个条件:$x^{T}Ax>0$
2-正定矩阵具有的特点
(这个可以参考第二十六课内容,如果有时间我会补充)
(1)它的所有的主元都必须是大于0的
(2)它的所有的特征值都是大于0的(实际上,特征值和主元的符号是相同的,比如,如果主元有三个正的,两个负的,那么特征值也是这样)
(3)它的所有的子行列式都是大于0的。
至于什么是子行列式,我们可以看一下下面的例子:
对于一个矩阵:
$\begin{bmatrix}2 & 3 & 1\\ 0 & 2 & 2\\ 1 & 1 & 1\end{bmatrix}$
那么它的子行列式有:$\begin{bmatrix}2\end{bmatrix}$,
$\begin{bmatrix}2 & 3\\ 0& 2\end{bmatrix}$
$\begin{bmatrix} 2 & 3 & 1\\ 0 & 2 & 2\\ 1 & 1 & 1\end{bmatrix}$
3-如何判断
根据上面的条件,那么自然而然就知道如何判断一个矩阵是不是正定矩阵:
(1)只有所有的主元都是正的,那么这个矩阵是正定矩阵
(2)所有的特征值是正的,那么这个矩阵是正定矩阵
(3)这个矩阵的所有子行列式是正的,那么这个矩阵是正定矩阵
(4)如果对于矩阵A, $x^{T}Ax>0$ (这个是根据定义式出发)
4-一个例子
4.1对于一个二阶矩阵$\begin{bmatrix}a & b\\ c & d\end{bmatrix}$,那么下面的四个条件都可以判断:
(1) $\lambda _{1}>0, \lambda _{2}>0$
(2) $a>0, \frac{ac-bd}{a}>0$
(3)$a>0, ac-bd>0$
(4) $x^{T}Ax>0$
4.2如下面一个矩阵:$\begin{bmatrix}2 & 6\\ 6 & 18\end{bmatrix}$
我们可以看到,第一列和第二列存在一个倍数的关系,所以这是一个奇异矩阵。
奇异矩阵一定有一个特征值是0, 另外一个特征值就等于迹减去这个特征值(这里是根据特征值之和等于主对角线的元素之和,也就是迹)
所以另外一个特征值是:20。
可以看到,一个特征值是0,另外一个特征值大于0,这个时候我们说这个矩阵是一个半正定矩阵。
这个时候我们根据$x^{T}Ax$,看一下其得到的结果:
$x=\begin{bmatrix}x_{1}\\ x_{1}\end{bmatrix} $
$f(x_{1},x_{2})=\begin{bmatrix} x_{1}&x_{2} \end{bmatrix}\begin{bmatrix}2 &6 \\ 6 & 18\end{bmatrix}\begin{bmatrix}x_{1}\\ x_{2}\end{bmatrix}$
$f(x_{1},x_{2})=2x_{1}^{2}+12x_{1}x_{2}+18x_{2}^{2}$
这个时候函数就相当于:
$f(x,y)=2x^{2}+12xy+18y^{2}$
这个时候我们画出它的图像如下:
matlab代码:
[x,y]=meshgrid(-100:0.1:100); z=2*x.^2+18*y.^2+12*x.*y; mesh(x,y,z); xlabel('x'),ylabel('y'),zlabel('z');
图像如下:
可以看到,它在(0,0)位置的值是0,但是这个时候并不是一个最低点,所形成的曲面是一个马鞍形的面。
四、几何含义
其实其几何含义我们在上面已经表示出来了。
4.1例子一
下面我们可以再举出来一个例子:
对于一个二维矩阵:$\begin{bmatrix}2 &6 \\ 6& 7\end{bmatrix}$,这个时候我们得到的 $x^{T}Ax$函数为:
$f(x,y)=2x^{2}+12xy+7y^{2}$
也可以知道这是一个非正定矩阵,我们按照上面的方法画出来,可以知道这也是一个马鞍面。
这也说明了,当一个矩阵不是正定矩阵的时候,这个时候所得到的函数$x^{T}Ax$并不是每一处都是大于0的,也无法得到最小值
4.2 例子二
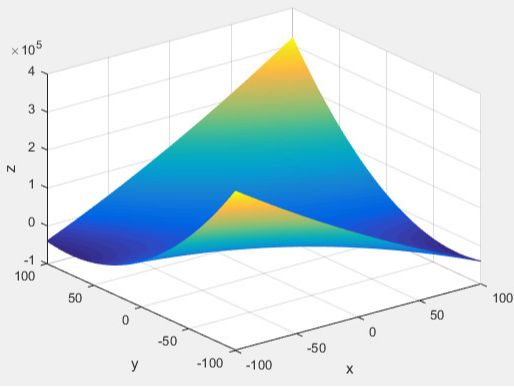
如果对于正定矩阵:$\begin{bmatrix}2 &6 \\ 6& 20\end{bmatrix}$
这个时候我们得到的函数是:
$f(x,y)=2x^{2}+12xy+20y^{2}$
我们得到下面的一个抛物面图像:
我们可以看到,对于一个正定矩阵,这个时候所得到的函数每一处都是大于0的。
其最小值在(0,0)处,且根据函数极值的只是我们知道:
在该点的函数一次导数为0,二次导数大于0
4.2.1<最小值判断>
对于一维函数来说是当其二次导数大于0的时候,一次函数等于0,这个时候函数存在极值。
而对于一个n维函数来说,只有当它的二阶导数矩阵是正定的时候,这个时候这个n维函数才存在最小极值点(上面两个例子已经说明了这一点)。
比如一个二阶函数f(x,y),那么它的二阶导数矩阵就是:
4.2.2利用配方法证明上述函数始终大于0:
我们可以利用配方法对于上面函数始终是大于0的做一个证明:
$f(x,y)=2x^{2}+12xy+20y^{2}\\=2(x+3y)^{2}+2y^{2}$
同时我们可以对矩阵$A=\begin{bmatrix}2 &6 \\ 6& 20\end{bmatrix}$做一个分解,分解为一个上三角矩阵(U)和一个下三角矩阵(L):
$A=\begin{bmatrix}1 & 0\\ 3 & 1\end{bmatrix}\begin{bmatrix}2 &6 \\ 0& 2\end{bmatrix}$
同时我们可以知道,这个矩阵的主元是:2, 2。
我们可以对比一下上面的函数和矩阵里面的系数。
这个时候我们可以先这样一个事实:
1-矩阵的主元是配方法里面平方外面的系数。
2-置换矩阵的系数是配方法平方里面的系数。
实际上,高斯的配方法就是对于矩阵消元的一个过程。
4.3 例子三
对于这样一个矩阵:
$A=\begin{bmatrix}2 &-1 &0 \\ -1 & 2 & -1\\ 0& -1 & 2\end{bmatrix}$
我们可以得到如下特点:
1-子行列式:
一阶子行列式:2
二阶子行列式:3
三阶行列式:4
2-根据行列式。其实我们可以得到主元:
2,1.5, 4/3
3-特征值: $2+\sqrt{2},2-\sqrt{2},2$
4- $ x^{T}Ax$
$f(x,y,z)=2x^{2}+2y^{2}+2z^{2}-2x_{1}x_{2}-2x_{2}x_{3}$
这个时候如果我们令f = 1 去截取这个图像(这是一个思维的图像)的时候,我们可以得到一个橄榄球样式的三维图像。
代码如下:
f = @(x,y,z)2*x.*x+2*y.*y+2*z.*z-2*x.*y-2*y.*z-1; % 函数表达式 [x,y,z] = meshgrid(-10:.2:10,-10:.2:10,-10:.2:10); % 画图范围 v = f(x,y,z); h = patch(isosurface(x,y,z,v,0)); isonormals(x,y,z,v,h) set(h,'FaceColor','r','EdgeColor','none'); xlabel('x');ylabel('y');zlabel('z'); alpha(1) grid on; view([1,1,1]); axis equal; camlight; lighting gouraud
可以看到,这里存在存在一个长轴,一个中轴,一个短轴,整个物体相对于这三个轴中任意两个所构成的平面对称。
这三个轴就是特征向量的方向,三个轴的长度是特征值的大小。
并且是对应的。
这个时候我们可以得到,$A=Q\Lambda Q^{T}$,也与刚才我们的表述相符合。
其中Q是正交矩阵,其中因为A是对称矩阵,所以将$A=Q\Lambda Q^{-1}$换成了$A=Q\Lambda Q^{T}$。
所以可以看到,对于一个函数,我们可以通过判断二阶矩阵的是否正定来判断是否存在其是否存在最小值。
如果是正定矩阵,对应的函数有最小值,且整个函数都是大于0的。
如果不是,则(0,0)不是最小值。
并且当我们截取函数的时候(令f = 一个常数)
这个时候我们得到的往往是一个特殊的形状,并且和特征值、特征向量相互联系。
而且通过高斯配方法的时候,其系数往往和矩阵的LU分解有关。