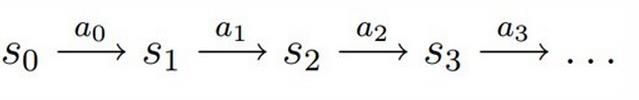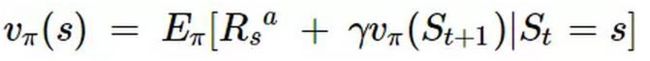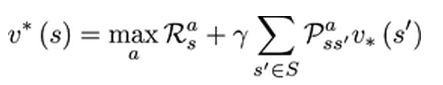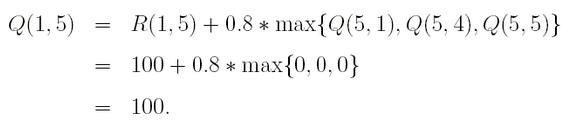强化学习详解与代码实现
本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/10789375.html
目录
1.引言
2.强化学习原理
2.1 强化学习定义(RL Reinforcement Learing)
2.2 马尔科夫决策过程(MDP Markov Decision Process)
2.3 贝尔曼方程(Bellman)
2.4 Q-Learning
3.代码实现与说明(python3.5)
4.运行结果
5.参考文献
1.引言
相信大家对由Google开发的AlphaGo机器人在2016年围棋对弈中击败韩国的围棋大师李世石还记忆犹新吧。当时,个人也确实被这场人机大战的结果深深震撼并且恐惧了。震撼是因为机器人的智慧超越了人类只有在科幻大片中看到,而今,这种故事却真真实实的发生在我们的现实中,恐惧是对未知的一种自然反应,也正是因为这种恐惧,我们才有了去探索未知的本能,去揭开AlphaGo机器人背后技术原理的面纱。相信大家已经猜到了AlphaGo机器运用的技术原理,不错,那就是强化学习(Reinforcement Learning)。
2.强化学习原理
2.1 强化学习定义
强化学习是一种通过交互的目标导向学习方法,旨在找到连续时间序列的最优策略。这个定义比较抽象(说实话,抽象的东西虽然简洁、准确,但是也非常难以理解)。举个容易理解的例子:
在你面前有两条路,自然就有两个不同方向,只有一条路,一个方向可以到达目的地,有个前提条件是你不知道目的地在他们当中的哪个方向?
是不是感觉很抓瞎,完全没办法。对的,如果按照这种场景,我们肯定是没办法的,但是如果给你个机会,让你在两个不同方向都去尝试一下,你是不是就知道哪一个方向是正确的。
强化学习的一个核心点就是要尝试,因为只有尝试了之后,它才能发现哪些行为会导致奖励的最大化,而当前的行为可能不仅仅会影响即时奖励,还会影响下一步的奖励以及后续的所有奖励。因为一个目标的实现,是由一步一步的行为串联实现的。
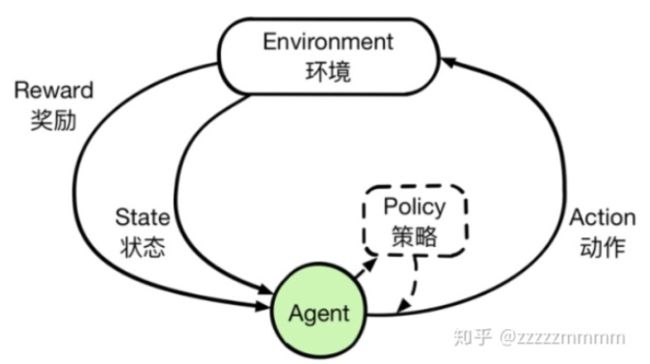
在上面的场景当中,涉及到了强化学习的几个主要因素:智能体(Agent),环境(Environment),状态(State)、动作(Action)、奖励(Reward)、策略(Policy)。
智能体(Agent):强化学习的本体,作为学习者或者决策者,上述场景是指我们自己。
环境(Environment):强化学习智能体以外的一切,主要由状态集合组成。
状态(State):一个表示环境的数据,状态集则是环境中所有可能的状态。比如,走一步就会达到一个新的状态。
动作(Action):智能体可以做出的动作,动作集则是智能体可以做出的所有动作。比如,走一步这个过程就是一个动作。
奖励(Reward):智能体在执行一个动作后,获得的正/负反馈信号,奖励集则是智能体可以获得的所有反馈信息。走正确就奖励,错误就惩罚。
策略(Policy):强化学习是从环境状态到动作的映射学习,称该映射关系为策略。通俗的理解,即智能体如何选择动作的思考过程称为策略。
第一步:智能体尝试执行了某个动作后,环境将会转换到一个新的状态,当然,对于这个新的状态,环境会给出奖励或者惩罚。
第二步:智能体根据新的状态和环境反馈的奖励或惩罚,执行新的动作,如此反复,直至到达目标。
第三步:智能体根据奖励最大值找到到达目标的最佳策略,然后根据这个策略到达目标。
要注意的是,智能体要尝试执行所有可能的动作,到达目标,最终会有所有可能动作对应所有可能状态的一张映射表(Q-table)。
这里借用知乎论坛关于强化学习各个因素关系的一幅图(https://www.zhihu.com/topic/20039099/intro)
原理我们明白了,接下来我们就来看大神如何将这些原理抽象出来,如何用数学的公式来表示的。
2.2 马尔科夫决策过程(MDP Markov Decision Process)
马尔科夫决策过程由5个因素组成:
S:状态集(states)
A:动作集(actions)
P:状态转移概率
R:即时奖励(reward)
γ:折扣系数(未来反馈的reward相比当下的重要性,在[0,1)之间)
决策过程: 智能体初始状态![]() ,选择一个动作
,选择一个动作![]() ,按概率转移矩阵
,按概率转移矩阵![]() 转移到下一个状态
转移到下一个状态![]() ,如此反复...
,如此反复...
表示在 ![]() 时刻的状态
时刻的状态 ![]() 能获得奖励的期望。
能获得奖励的期望。
2.3 贝尔曼方程(Bellman)
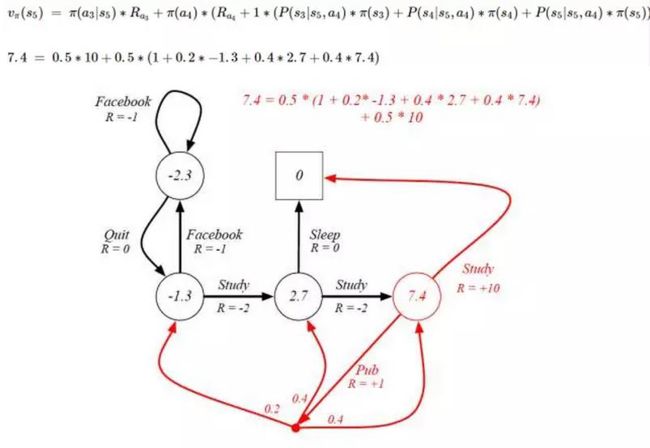
贝尔曼方程是更一般的状态价值函数表达式,它表示当前状态的价值由当前的奖励和下一状态的价值组成。这里借用某位大神的一幅图形象说明:
这里假定期望都是 0.5,7.4对应的状态 ![]() 的下一个状态是
的下一个状态是 ![]() (红色圆圈) 和
(红色圆圈) 和 ![]() (0) 。
(0) 。
![]() 下一个状态分别是
下一个状态分别是 ![]() ,
,![]() ,
,![]() ,
,![]() 没有下一个状态。
没有下一个状态。
![]() 对应的价值
对应的价值 ![]() = 当前的奖励 + 下一状态的价值
= 当前的奖励 + 下一状态的价值
上述图计算 ![]() 价值在表述上有点不对,没有将即时奖励和下一状态价值分开,在理解上容易造成混乱。
价值在表述上有点不对,没有将即时奖励和下一状态价值分开,在理解上容易造成混乱。
所以 ![]() 对应的价值
对应的价值 ![]() = 0.5 * (10 + 1) + 0.5 * (0.2 *(-1.3)+ 0.4 * 2.7 + 0.4 * 7.4 )
= 0.5 * (10 + 1) + 0.5 * (0.2 *(-1.3)+ 0.4 * 2.7 + 0.4 * 7.4 )
贝尔曼最优化方程:
表示在某个状态下最优价值函数的值,也就是说,智能体在该状态下所能获得累积奖励值得最大值。
2.4 Q-Learning
学习在一个给定的状态时,采取了一个特定的行动后,所得到的回报 ![]() ,然后遍历所有可能的行动,得到所有状态的回报 Q (Table)。
,然后遍历所有可能的行动,得到所有状态的回报 Q (Table)。
其实,每个 ![]() ==
== ![]() 。Q-Table生成的算法流程:
。Q-Table生成的算法流程:
1. 初始化Q-Table 每个状态(s)对应的回报为 0;
2. 随机选取一个状态(s)作为遍历的起始点;
3. 在当前状态(s)的所有可能的行动(A)中按顺序遍历每一个行动(a);
4. 移动到下一个状态 ![]() ;
;
5. 在新状态上选择 Q 值最大的那个行动(a1);
6. 用贝尔曼方程更新Q-Table中相应状态-行动对应的价值(![]() )。按顺序遍历第3步其他可能的行动,重复第3 - 6步;
)。按顺序遍历第3步其他可能的行动,重复第3 - 6步;
7. 将新状态设置为当前状态,然后重复第2 - 6步,直到到达目标状态;
这里注意有两层循环:
外层:遍历所有状态;
内层:遍历每个状态的所有可能的行动;
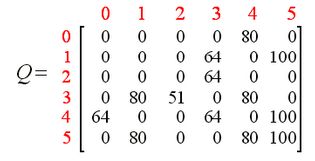
举个样例,左边是Q-Learning过程(R:奖励),中间是state = 1,action = 5生成Q-Table结果,右边是最终Q-Table结果。
3.代码实现与说明(python3.5)
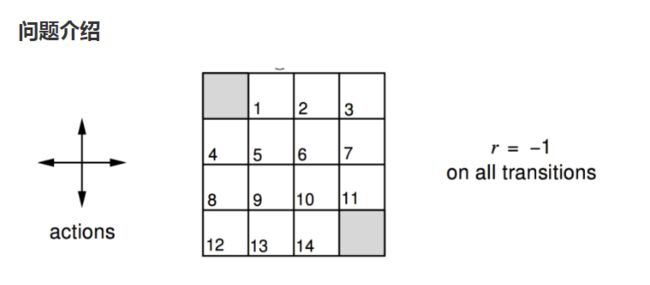
这里举一个例子来加深对强化学习原理的理解。游戏规则如下:以灰色两个框作为目标出口,图中有16个状态(加上目标出口),每个状态都有4个方向(上,下,左,右),找出任一状态到目标出口的最优方向(如下图)。
gridworld.py
1 import io 2 import numpy as np 3 import sys 4 from gym.envs.toy_text import discrete 5 6 UP = 0 7 RIGHT = 1 8 DOWN = 2 9 LEFT = 3 10 11 class GridworldEnv(discrete.DiscreteEnv): 12 """ 13 Grid World environment from Sutton's Reinforcement Learning book chapter 4. 14 You are an agent on an MxN grid and your goal is to reach the terminal 15 state at the top left or the bottom right corner. 16 17 For example, a 4x4 grid looks as follows: 18 19 T o o o 20 o x o o 21 o o o o 22 o o o T 23 24 x is your position and T are the two terminal states. 25 26 You can take actions in each direction (UP=0, RIGHT=1, DOWN=2, LEFT=3). 27 Actions going off the edge leave you in your current state. 28 You receive a reward of -1 at each step until you reach a terminal state. 29 """ 30 31 metadata = {'render.modes': ['human', 'ansi']} 32 33 def __init__(self, shape=[4,4]): 34 if not isinstance(shape, (list, tuple)) or not len(shape) == 2: 35 raise ValueError('shape argument must be a list/tuple of length 2') 36 37 self.shape = shape 38 39 nS = np.prod(shape) 40 nA = 4 41 42 MAX_Y = shape[0] 43 MAX_X = shape[1] 44 45 P = {} 46 grid = np.arange(nS).reshape(shape) 47 it = np.nditer(grid, flags=['multi_index']) 48 49 while not it.finished: 50 s = it.iterindex 51 y, x = it.multi_index 52 53 # P[s][a] = (prob, next_state, reward, is_done) 54 P[s] = {a : [] for a in range(nA)} 55 56 is_done = lambda s: s == 0 or s == (nS - 1) 57 reward = 0.0 if is_done(s) else -1.0 58 59 # We're stuck in a terminal state 60 if is_done(s): 61 P[s][UP] = [(1.0, s, reward, True)] 62 P[s][RIGHT] = [(1.0, s, reward, True)] 63 P[s][DOWN] = [(1.0, s, reward, True)] 64 P[s][LEFT] = [(1.0, s, reward, True)] 65 # Not a terminal state 66 else: 67 ns_up = s if y == 0 else s - MAX_X 68 ns_right = s if x == (MAX_X - 1) else s + 1 69 ns_down = s if y == (MAX_Y - 1) else s + MAX_X 70 ns_left = s if x == 0 else s - 1 71 P[s][UP] = [(1.0, ns_up, reward, is_done(ns_up))] 72 P[s][RIGHT] = [(1.0, ns_right, reward, is_done(ns_right))] 73 P[s][DOWN] = [(1.0, ns_down, reward, is_done(ns_down))] 74 P[s][LEFT] = [(1.0, ns_left, reward, is_done(ns_left))] 75 76 it.iternext() 77 78 # Initial state distribution is uniform 79 isd = np.ones(nS) / nS 80 81 # We expose the model of the environment for educational purposes 82 # This should not be used in any model-free learning algorithm 83 self.P = P 84 85 super(GridworldEnv, self).__init__(nS, nA, P, isd) 86 87 def _render(self, mode='human', close=False): 88 """ Renders the current gridworld layout 89 90 For example, a 4x4 grid with the mode="human" looks like: 91 T o o o 92 o x o o 93 o o o o 94 o o o T 95 where x is your position and T are the two terminal states. 96 """ 97 if close: 98 return 99 100 outfile = io.StringIO() if mode == 'ansi' else sys.stdout 101 102 grid = np.arange(self.nS).reshape(self.shape) 103 it = np.nditer(grid, flags=['multi_index']) 104 while not it.finished: 105 s = it.iterindex 106 y, x = it.multi_index 107 108 if self.s == s: 109 output = " x " 110 elif s == 0 or s == self.nS - 1: 111 output = " T " 112 else: 113 output = " o " 114 115 if x == 0: 116 output = output.lstrip() 117 if x == self.shape[1] - 1: 118 output = output.rstrip() 119 120 outfile.write(output) 121 122 if x == self.shape[1] - 1: 123 outfile.write("\n") 124 125 it.iternext()
ValueIteration.py
1 import numpy as np 2 import gridworld as gw 3 4 5 env = gw.GridworldEnv() 6 # V表是当前状态走下一步时最大回报(先求下一步不同方向的回报,然后求最大值); 7 # Q表是计算所有状态所有可能的走法; 8 def value_iteration(env, theta=0.0001, discount_factor=1.0): 9 """ 10 Value Iteration Algorithm. 11 12 Args: 13 env: OpenAI environment. env.P represents the transition probabilities of the environment. 14 theta: Stopping threshold. If the value of all states changes less than theta 15 in one iteration we are done. 16 discount_factor: lambda time discount factor. 17 18 Returns: 19 A tuple (policy, V) of the optimal policy and the optimal value function. 20 """ 21 22 def one_step_lookahead(state, V): 23 """ 24 Helper function to calculate the value for all action in a given state. 25 26 Args: 27 state: The state to consider (int) 28 V: The value to use as an estimator, Vector of length env.nS 29 30 Returns: 31 A vector of length env.nA containing the expected value of each action. 32 """ 33 """ 34 游戏规则: 0,15 作为出口 ,找出每个状态(16个)到达出口最快的一步 35 0 o o o 36 o x o o 37 o o o o 38 o o o 15 39 """ 40 # env.P 是个初始状态table 在状态0,15 有奖励,其他都是惩罚 -1 41 # 每个action回报(上,下,左,右) = 概率因子 *(即时奖励 + 折扣因子 * 下个状态回报(当前行动到达的下个状态) 42 A = np.zeros(env.nA) 43 for a in range(env.nA): 44 for prob, next_state, reward, done in env.P[state][a]: 45 A[a] += prob * (reward + discount_factor * V[next_state]) 46 return A 47 48 #每次获取16个状态的回报V(矩阵), 49 # 找到当前状态某个行为的最大回报与当前状态历史回报最小值 < 超参theta,就结束循环。 50 # 这时状态V就是每个状态某个即将行为的最大回报 51 V = np.zeros(env.nS) 52 while True: 53 # Stopping condition 54 delta = 0 55 # Update each state... 56 # 有16个状态,每次都需要全部遍历 57 for s in range(env.nS): 58 # Do a one-step lookahead to find the best action 59 A = one_step_lookahead(s, V) 60 best_action_value = np.max(A) 61 # Calculate delta across all states seen so far 62 delta = max(delta, np.abs(best_action_value - V[s])) 63 # Update the value function 64 V[s] = best_action_value 65 # Check if we can stop 66 if delta < theta: 67 break 68 #(16,4) 69 # Create a deterministic policy using the optimal value function 70 policy = np.zeros([env.nS, env.nA]) 71 for s in range(env.nS): 72 # One step lookahead to find the best action for this state 73 A = one_step_lookahead(s, V) 74 best_action = np.argmax(A) # 最大值对应索引 75 # Always take the best action 76 policy[s, best_action] = 1.0 77 78 return policy, V 79 80 policy, v = value_iteration(env) 81 82 print("Policy Probability Distribution:") 83 print(policy) 84 print("") 85 86 print("Reshaped Grid Policy (0=up, 1=right, 2=down, 3=left):") 87 # 返回的是最大值的索引 axis = 1 列 88 print(np.reshape(np.argmax(policy, axis=1), env.shape)) 89 print("")
4.运行结果
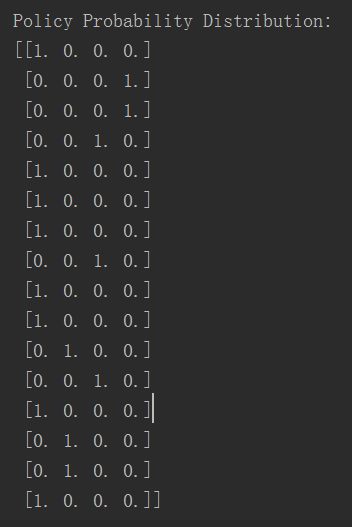
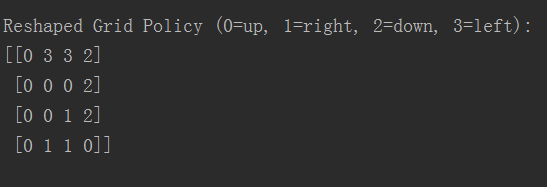
游戏规则有16个状态(state),每个状态有4个行动方向(action),因此Q-Table大小是(16, 4),具体生成结果如下图:
最终每个状态最佳行动方向大小(4, 4),结果为
5.参考文献
1.https://www.zhihu.com/topic/20039099/intro
2.http://baijiahao.baidu.com/s?id=1597978859962737001&wfr=spider&for=pc
3.https://applenob.github.io/gridworld.html