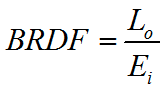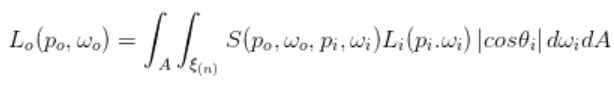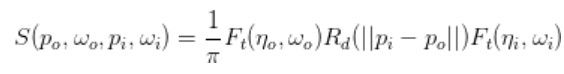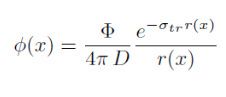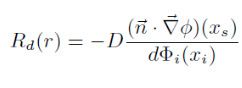Lambert
Lambert不包括任何镜面属性,对粗糙物体来说,这项属性是非常有用的,它不会反射出周围的环境。简单来说是一种“磨砂效果”。
Lambert材质可以是透明的,可以在光线追踪渲染中发生折射,但是如果没有镜面属性,该类型就不会发生折射。
平坦的磨光效果可以用于砖或混凝土表面。它多用于不光滑的表面,是一种自然材质,常用来表现自然界的物体材质,如:木头、岩石等。
Lambert radiator
一般来说,辐射面源射向各个方向的辐射亮度是不同的,具有方向性。若辐亮度不随方向x(x为辐亮度方向与平面法线之间的交角)变化,这类辐射体就称为朗伯辐射体(Lambert radiator),也称为余弦辐射体。
朗伯辐射体发光强度的空间分布符合余弦定律的发光体(不论是自发光或是反射光),其在不同角度的辐射强度会依余弦公式变化,角度越大强度越弱。
一个均匀的球形余弦发光体,从远处的观察者看来,与同样半径同样亮度的一个均匀发光圆盘无异。太阳看起来近似像一个亮度均匀的圆盘,这表明它接近于一个余弦发光体。此外,日常生活中常见的光源,许多也接近于余弦发光体。
Lambert 光照模型
Lambert光照模型(Lambert illumination model)用于纯粹的漫反射表面的物体,光源照射到物体表面后,向四面八方反射,产生的漫反射效果。
这是一种理想的漫反射光照模型,比如磨砂的玻璃表面,观察者的所看到的反射光和观察的角度无关,这样的表面称为Lambertian。高端一点的说法就是他表面的亮度是各向同性的。
Phong光照模型
对于漫反射的物体表面,使用Lambert就足够,但是实际生活中并不存在这种理想的漫反射材质,所以Bui Tuong Phong就提出了Phong模型。
Blin-Phong光照模型
这个模型作为Phong光照模型的改进,在表现上基本与Phong模型一致,但是性能上却优化了很多。下图为对比图:
BRDF
双向反射分布函数(Bidirectional Reflectance Distribution Function,BRDF)用来定义给定入射方向上的辐射照度(Irradiance)如何影响给定出射方向上的辐射率(Radiance)。
更笼统地说,它描述了入射光线经过某个表面反射后如何在各个出射方向上分布——可以是从理想镜面反射到漫反射、各向同性(Isotropic)或者各向异性(Anisotropic)的各种反射。
光线照到一个物体,首先产生了反射,吸收和透射,所以BRDF的关键因素即为多少光被反射、吸收和透射(折射)了,是怎样变化的。这时的反射多为漫反射。
然而,要想知道这些光线反射透射的变化就需要清楚三样东西——物体的表面材质、光线的波长(即它是什么样的光,是可见太阳光,节能灯光还是紫外线)和观察者与物体之间的位置关系。
三维世界角度可以类似是球体的,光线角度除了纵向180°的变化,还有横向360°的不同发散方向。会有相应的入射光,反射光,入射角和反射角,它们在物体表面的法平面和切平面上的关系成为了BRDF的关键参数。
由于人类眼睛对光的特殊敏感性,我们之所以能看到物体都是通过光线在物体上的发射和转移实现的。而双向反射分布这样的函数表示可以更好地描述光线在物体上的变化,反射光线同时发向分布在法线两边的观察者和光源两个方向,从而使人在计算机等模拟环境下,视觉上可以看到更好的物体模拟效果,仿佛真实的物体存在。
在计算机图形学中实现BRDF理论模型的一个方法是用微小面元对物体表面进行建模,每一个小平面都是表面上的一个小平面镜,具有随机的大小和角度。这些小平面通常被赋予一个高斯分布的尺寸和角度。
P.S.
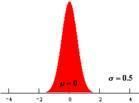
正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution),最早由A.棣莫弗在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。
是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。
BSSRDF
对于一般的材质采用BRDF(bidirectional reflectance distribution function)可以很好的表达,而对于皮肤来说因为其具有半透明属性光线会在皮肤的表层进行多次散射,散射根据其通过的路径衰减,简单来说就是光线会扩散到周围,这对于表现皮肤的质感起到很大作用。
模拟透明物体的方法有很多,例如Volumetric Path Tracing,Volumetric Photon Mapping和BSSRDF(Bidirectional Surface Scattering Reflectance Distribution Function)。BSSRDF目前是主流技术,其和BRDF的不同之处在于,BSSRDF可以指定不同的光线入射位置和出射的位(见下图)。Jensen在2001年的论文是次表面材质建模最重要的一篇论文[Jensen, Henrik Wann, Stephen R. Marschner, Marc Levoy, and Pat Hanrahan. 2001. "A Practical Model for Subsurface Light Transport." In Proceedings of SIGGRAPH 2001.],推导了许多重要的物理公式,计算模型,渲染时的参数转换,以及测量了许多生活中常见材质的散射系数等等。大部分后来的论文都是在基于这篇文章中的理论的一些提升。
对于BRDF模型来说,一次反射光照的计算是在光线交点的法线半球上的球面积分。而对于BSSRDF来说,每一次反射在物体表面上每一个位置都要做一次半球面积分,是一个嵌套积分。
其中BSSRDF的定义是:
Rd只接受一个标量参数,这个参数的意义是光线入射位置和初设位置的曼哈顿距离。直观的理解就是,BSSRDF尝试将光线在物体表面内部中数千次的散射后所剩余的能量用一个基于入射点和出射点之间距离的函数去近似只接受一个标量参数,这个参数的意义是光线入射位置和初设位置的距离。也就是说,BSSRDF尝试将光线在物体表面内部中数千次的散射后所剩余的能量用一个基于入射点和出射点之间距离的函数去近似。这个近似则是基于几个假设:
1. 次表面散射的物体是一个曲率为零的平面
2. 这个平面的厚度,大小都是无限
3. 平面内部的介质参数是均匀的
4. 光线永远是从垂直的方向入射表面。
正因为有这些假设,所以很容易把出射光的强度与出射点和入射点之间的距离用一个函数去近似。而真实的模型往往比理想中要复杂的多,光线也有可能从各个角度入射,因此通过BSSRDF渲染的结果会有一定误差。
Rd的求解非常复杂,通过近似可以得到
有的可以得到:
可以看出和自然指数有关系。
Cook-Torrance光照模型
上面所说模型都只能运用在理想的材质下,要么理想漫反射,要么理想镜面反射,这样渲染出来的物体就很假,真实的情况是漫反射和镜面反射都需要依据材质特征和物体表面微平面分布(Microfacet Distribution)特征。
Cook-Torrance 光照模型将物体粗糙表面( rough surface)看作由很多微小平面(微平面)组成,每一个微平面都被看作一个理想的镜面反射体,物体表面的粗糙度由微平面斜率的变化来衡量。一个粗糙表面由一系列斜率变化很大的微平面组成,而在相对平滑的表面上微平面斜率变化较小。