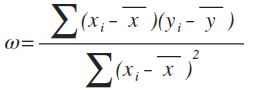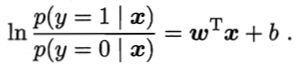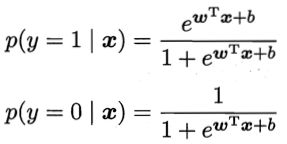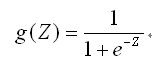积跬步以致千里,积怠惰以致深渊
注:本篇文章在整理时主要参考了 周志华 的《机器学习》。
主要内容
线性模型(linear model)试图学得一个通过属性的线性组合来进行预测的函数。其形式简单、易于建模,许多功能更为强大的非线性模型可在线性模型的基础上通过引入层级结构或高维映射而得。
基本形式
给定由d个属性描述的示例,即:
一般用向量形式写成:
其中xi是样本的第i个属性的属性值,wi是线性模型对第i个属性的权重,b是模型的线性偏移量。此外,由于ω直观表达了各属性在预测中的重要性,因此线性模型有很好的可解释性。
线性回归
“线性回归” (linear regression) 试图学得一个线性模型以尽可能准确地预测实值输出标记。
因为是函数训练,所以我们在训练之前需要将离散值属性转换为连续值属性。并且该属性的属性值之间是否存在“序”关系,会有不同的转换方式。如果是有序属性,我们会根据属性序数高低给予一个数字序列,比如身高,具有“高、中等、矮”三个有序属性值,那么我们就能将其转换为{1,0.5,0};如果属性值之间没有序列,我们要将这k个属性值转为k维向量,比如天气,“下雨、晴天、多云”三个属性值之间并没有序列关系,那么就应该将其转换为3维向量,(1,0,0),(0,1,0),(0,0,1)。
在对数据进行转换之后,为了能生成线性回归模型,我们应该如何确认w和b呢?通过分析线性回归的函数目的,我们发现线性回归是为了能使得生成的回归函数能更贴近样本标签,也就是说当训练出来的模型f(x)和真实值y之间的误差最小时,对应于训练出来的模型f(x)和真实值y之间欧几里得距离或称“欧氏距离”(Euclidean distance)最小时,该线性回归模型就是我们要的,此时我们称之为函数收敛。该模型求解方法称为“最小二乘法”(least square method)。在线性回归中,最小二乘法就是试图找到一条直线,使所有样本到直线的欧氏距离之和最小 (sum of square) 。
应该如何使得距离最小呢?我们通过对距离之和求导,当导数为0时,说明原函数达到了一个极值(因为是凹函数,所以该极值是最小值)。
广义线性模型
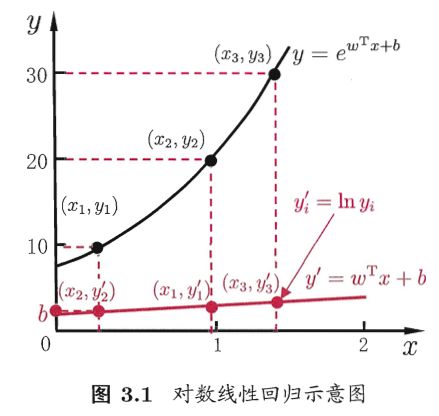
线性回归函数可以简写为:y = wx + b,这是用模型的预测值去逼近真实标记y。那么我们能不能令预测值去逼近y的衍生物呢?基于这样的考虑,我们就得到了线性回归的各种变型函数。
比如,假设我们认为示例所对应的输出标记是在指数尺度上变化的,那么就可将输出标记的对数作为线性模型逼近的目标,即可得到“对数线性回归”(log-linear regression):
ln(y) = wx + b
更一般地,考虑单调可微函数g,令:
g(y) = wx + b
这样得到的模型称为“广义线性模型”(generalized linear model),其中函数g称为“联系函数”(link function)。不同的联系函数会构成不同的线性回归模型。广义线性模型的参数估计常通过加权最小二乘法或极大似然估计法进行。
逻辑回归
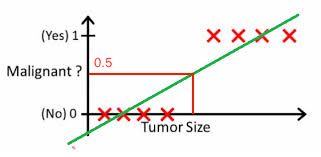
同样,当我们根据肿瘤的大小判断一个肿瘤是不是恶性的时候,输出结果只有是或者否,分别用1和0表示。给定的样本点,并且我们使用传统的线性回归问题解决拟合的图像如下:
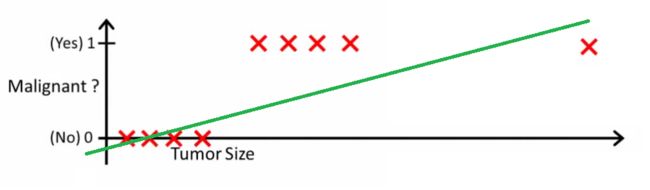
图像中我们可以根据拟合曲线,当输出值大于0.5(根据图像判断的值)的时候,确定输出的为恶性(即为1);当输出值小于0.5(根据图像上的值)的时候,确定输出的为良性(即为0)。但是,当我们有新的样本点加入的时候,如下图:
我们会发现,对于新的拟合曲线使用上面的方法和标准(0.5)并不能很好的作出预测。因此我们判断这种形式的曲线不合理。
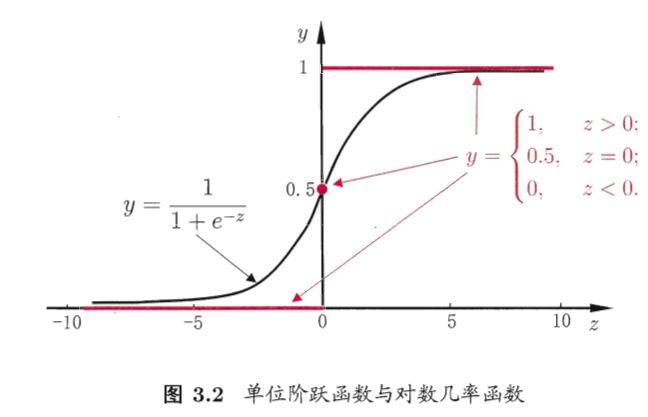
针对以上问题,我们提出当 g(y) = ln( y / (1-y) ) 时,我们得到了“对数几率回归”(logit regression),也称“逻辑回归函数”。通过联系函数,我们可以看出该模型实际上是在用线性回归模型的预测结果去逼近真实标记的对数几率。
同样我们需要确定w和b,我们将y视为后验概率估计p(y=1|x),则
显然
于是,我们可通过“极大似然法” (maximum likelihood method) 来估计w和b。即令每个样本属于其真实标记的概率越大越好。
注解
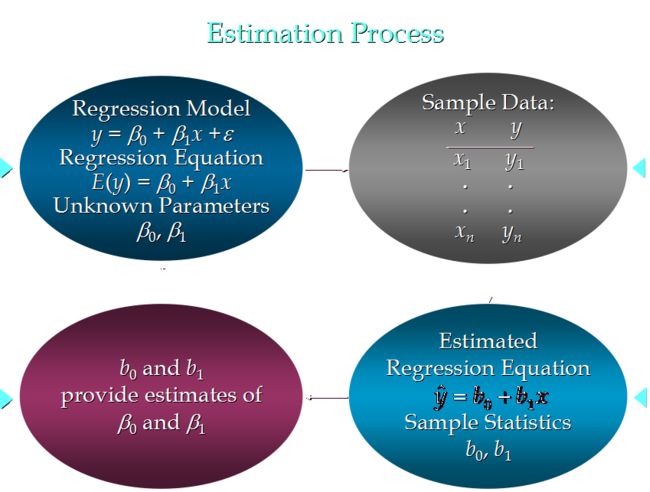
简单线性回归模型
被用来描述因变量 (y) 和自变量 (x) 以及偏差 (error) 之间关系的方程叫做回归模型。
错误项ε满足期望值为0的正态分布,则E(y)=β0+β1x。其中,E(y)是一个给定x值下y的期望值(均值)。假定估计线性回归方程̂y=b0+b1x。程̂y是我们训练得出线性模型在自变量x下的估计值。
关于偏差ε的假定:
1、是一个随机的变量,均值为0;
2、ε的方差 (variance) 对于所有的自变量x是一样的;
3、ε的值是独立的;
4、ε满足正态分布。
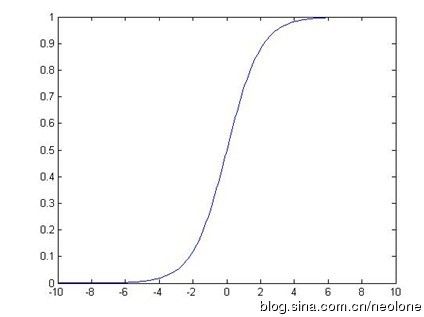
Sigmoid函数
由于函数定义域为0~∞,值域为0~1,而且我们想要一个非线形的转化关系。因此我们引入Sigmoid函数令曲线平滑化,处理二值数据。
梯度下降(Gradient Descent)
总结
线性模型是一个形式简单、易于建模的机器学习模型,因为w直观表达了各属性在预测中的重要性,因此线性模型有很好的可解释性
线性回归背后的逻辑是用模型的预测值去逼近真实标记y,并通过计算训练样本在向量空间上距离模型线的欧式距离之和的最小值来确定参数w和b
线性回归可写成广义线性模型形式:g(y) = wx + b,通过选择不同的联系函数g(.)会构成不同的线性回归模型
在遇到多分类学习任务时,基本的解决思路是“拆解法”,即将多分类任务拆为若干个二分类任务求解
当不同类别的样例数不同时,会造成类别不平衡问题,解决该问题的基本策略是对数据进行“再缩放”