巴菲特曾说:他相信概率,但他也很含蓄的说中国人更喜欢运气。
那么我们就来看看到底概率是什么,让巴爷如此这般宠幸。
什么是概率论:
是根据大量同类随机现象的统计规律,对随机现象出现某一结果的可能性作出一种客观的科学判断,对这种出现的可能性大小做出数量上的描述;比较这些可能性的大小、研究它们之间的联系,从而形成一整套数学理论和方法。
(还记得我上一篇反复唠叨的,把模糊的概念弄清楚的重要性了?你一定忘了。)
我估计有人看到概率论这三个字就头疼了吧?
是的,头疼,怎么办?
有办法,把它弄明白了,你再看到这三个字就肯定不头疼了,所以说,概率论是良药,不只让你避免上当受骗还能包治头疼病。
那么如果要弄明白它,首先我们必须先知道“随机事件”是个什么鬼?
这鬼的特点是试验之前我们不能知道结果,例如买彩票,可能中可能不中,每天火车站,机场每天出现的人数都是随机的自然现象。
那么随机事件是否有规律可循?
几个世纪前的确有2位统计学家们热爱做这个事,他们用投币试验这个试验结果给了 我们准确的回答:小伙伴们,不用愁,数字解你犹。
实验得出的结论就是随机现象在相同的条件下,大量的重复实验中呈现的规律性,是统计规律性,由此看来概率论和统计学也是一对好基友哦!
让我们来先看一看投硬币这个简单的实验吧:
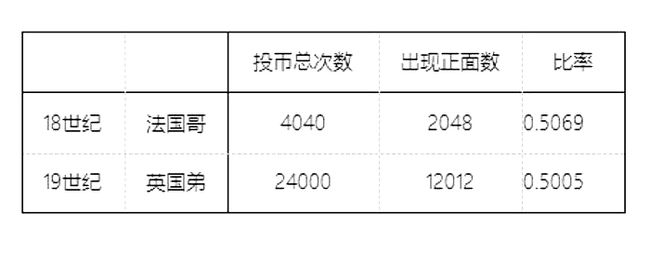
18世纪的法国和19世纪的英国,两位哥给我们做了一个投硬币的随机试验。
一个哥做了4040次,另一个哥做24000次,我服了我的这两位哥,首先感谢这两哥,在没有任何赌注的前提下,做了这么多次重复的动作还不吐,也就是想让我们知道,无论抛多少次硬币,抛的次数越多,正面出现的概率越接近50%,同理,反面也一样。
下面我是手动统计列出来2位哥投了硬币次数和出现的“正面”的次数以及各自概率数据,表示我对2位哥的敬意!
此刻我要向能坚持看到这里的小伙伴致敬,为此,让我们暂停,休息一下,来个小运动!
摸摸口袋,拿出一枚硬币,跟我一起玩一次抛硬币游戏吧!
你们还记得吗?在我们小时候,大部分人都玩这个游戏,基本”正面”都是定义为赢方,富裕点的玩法就是拿糖做赌注,穷一点的玩就是拿扑克牌做赌注,此刻回想一下,巴爷说的没错,从小我们就学会玩赌博游戏了,并且,长大了之后,也仍然有一大部分人相信运气,甚至还如此痴迷。
我就在写这篇文章的时候,也顺手拿了一枚1元硬币,每次都是抛投6次硬币,我一共做了2次同样的试验,然后简单统计一下每次我得到正面的比率。
奇迹出现了,我第一次连续抛了6次硬币,结果全部是正面,那叫一个心花怒放,就着第一次的好运气,我又连续抛了6次,结果又是6次全部正面。此刻,我听到了你们的欢呼声,参杂着一种蠢蠢欲动,然后就是空气里弥漫着一种气氛,一种弥漫的会促使你过分相信运气这玩意的气氛,然后便觉得周身都围绕着一个叫”好运气“的妹子和一个叫”赚大钱“的姑娘,直到这两迷一般的妞儿叫做你痴一样的决定压上全部,结果是,我不但血本无归,说不定还债台高筑呢。
幸好,此刻概率先生抽了我一嘴巴,说醒醒吧!我的妹!
游戏结果,回到正题:
其实通过这个小游戏,你们可以发现在实验次数相对较少的情况下,“正面”出现的概率波动很大的,也就是不确定性极强,那么只有在次数逐渐增大,概率才会相对稳定在50%左右,这个发现反射到股票价格波动上,你这会儿一定会明白了一个道理,短期股票价格的波动,是如此不确定,同时股票市场价格的波动是随机的,像一个在广场上行走的人一样,价格的下一步将走向哪里,是没有规律的。证券市场中,价格的走向受到多方面因素的影响。一件不起眼的小事也可能对市场产生巨大的影响,更何况近年来随时出现的大胖黑天鹅全球胡乱飞翔,它的出现概率比过往开始逐渐变大,如果黑胖天鹅出来的次说多了,那么它就不再是那种发生机率很小的小概率事件了,估计《黑天鹅》这本书需要改名了。也就是说,金融圈还只是个圈,而且金融圈都被几个数学家的“假说”玩坏了,不同的年代,不同的数学家们提出的“随机市场假说”,被普林斯顿大学的一位叫伯顿的写在该圈畅销书《漫步华尔街》里之后,就成了该圈的宝典了。但,我说”假说“就是”假说“,连“理论”二字都没勾搭上,也只算圈规了。
话说回来了,我们在从长时间的价格走势图上也可以看出,价格的上下起伏的机会差不多是均等的。
也就是说,如果把投币“实验次数的数量”用“时间”和“空间”来替换,那么长期来看,价格的预测还是可能的,而且预测时间拉的越长,预测难度越低。
希望来了对不对,对不对,对不对?重要的话说3遍!
一个小小的投币试验,告诉我们一个很简单的事实,不要过分相信运气,甚至痴迷它,它该来的时候会来。有这么一句老话叫:“机会总是会给有准备的人而准备的”,还有一句巴爷的我觉得用在这会儿也贴切“你想要的东西,你得配得上它”。那么你想要的那个机会或者叫运气,来了之前,你得有识别它的能力,识别的能力都没有,即使机会如四月的绽放的樱花漫天飞你都看不到。
世界如此之大,而人与人的区别也只不过是认知区别,你认为是好的事情,他认为是坏,你觉得炒股是赌博,而他认为是投资,你觉得帝都机会多,有发展空间,而他认为这个城市房子贵,生活压力大,生活中,我们还有许多许多我们不知道的和被忽略的认知偏差,如果你不善于发现和纠正它,小的会犯错,大的酿苦果都说不定呢。
就比如在赌博这件事情上,有些人根本就不计算,甚至想都不想,很多人也不知道自己在赌什么,真是因为赌徒的知识欠缺,他们无法理解和接受概率学上的重要概念”独立事件”,于是肾上腺彪飞的时候觉得漫天的银子在朝他飞奔而来,不但押上全部,还要借钱炒股炒房,这明明就是炒焦你的后半生,也许有些人炒的更诗意一些,你会看到他从高楼上一跃而下,随风飘荡,说不定去了诗一样的远方。
如果你看到了这里,我再次给你敬意,说明你不是个伸手党,但你一定会问我,你说的可以长期预测的那个希望在哪里?
我的回答:耐心
巴菲特和他的好基友查理芒格的最优品质就是:耐心
2017.03.31
Lola
魔都
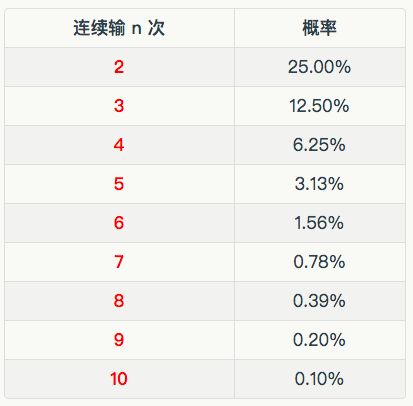
这里“手动福利”,送给赌徒们,这就是无知无畏的代价:看你几次输光光!
赌赢和赌输的概率是:根据赌徒谬论,连续几次都输,会在第几次全部输光,由图可以看出是第6次就差不多了。
再送2个跟概率有关的小案例:
1)这是巴爷的:
有人质疑巴菲特的投资策略只是运气好而已,他讲了一个有关概率的故事:一群猪共有128000只,分别来自全世界各农场举行丢铜板比赛,投出正面的晋级,投出反面的淘汰,经过九回合后,只剩下250只猪晋级,有人认为那250只猪只是运气好而已。如果你发现晋级的250只猪有200只全是某农场来的,那你就必须问:那个农场喂猪的饲料有没有特别之处?
2)而我喜欢的是这个:送给我自己
A、B、C三牛仔连环决斗,规则如下:1、抽签决定开枪顺序;2、有开枪权者可以自行选择射杀对象;3、每次只能开一枪;4、直至剩下一个人。已知A和B百发百中,C的命中率是50%。请问谁活下来的几率最大?是多少?
答:抽签顺序可能有六种--ABC,ACB、BAC、BCA、CAB、CBA。前四种,A和B都会选择先开枪干掉对方,然后轮到C开枪,其50%得手。后两种,C先开枪,他最明智的办法是对天开一枪(这个是本题亮点,和概率无关哈),然后留着AB彼此灭一个,然后在由C开枪,其50%得手。