贵州茅台（600519）股价预测——金融时序模型(ARIMA)

很久没有更新了！！！咱再忙也不能忘记学习啊~

最近无论同事也好，朋友也好，都提到一只股票"贵州茅台"，所以就拿来试水，接下来会介绍下简单介绍下该模型概念，以及python如何使用该模型。

基本概念

ARIMA模型的全称叫做自回归移动平均模型，全称是(ARIMA, Autoregressive Integrated Moving Average Model)。也记作ARIMA(p,d,q)，是统计模型(statistic model)中最常见的一种用来进行时间序列预测的模型。

建模步骤

1. 获取被观测系统时间序列数据；
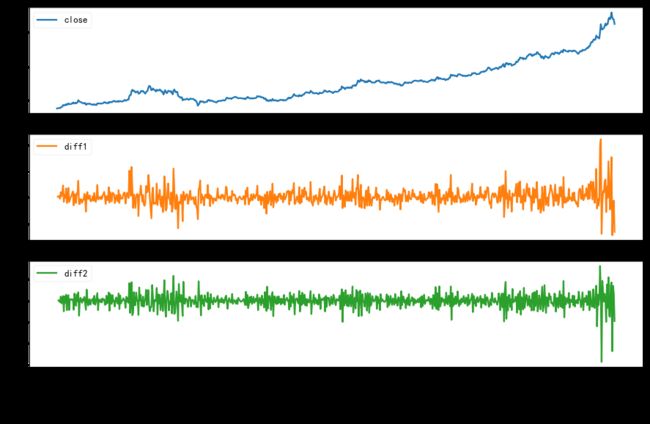
2. 对数据绘图，观测是否为平稳时间序列；对于非平稳时间序列要先进行d阶差分运算，化为平稳时间序列；
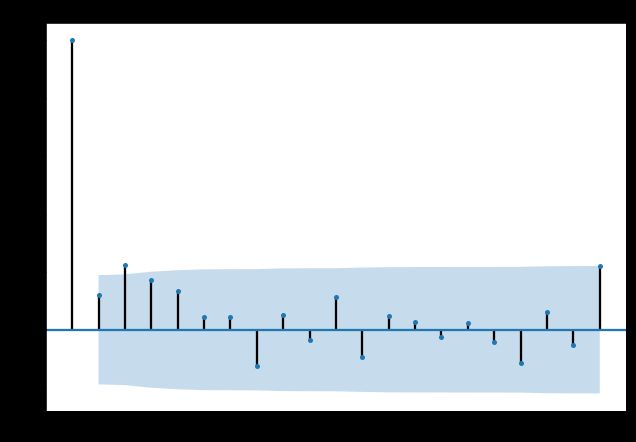
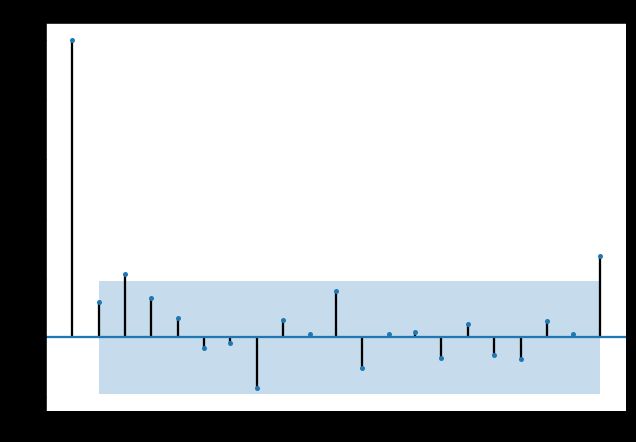
3. 经过第二步处理，已经得到平稳时间序列。要对平稳时间序列分别求得其自相关系数ACF和偏自相关系数PACF，通过对自相关图和偏自相关图的分析，得到最佳的阶层 p 和阶数 q
4. 由以上得到的d、q、p，得到ARIMA模型。然后开始对得到的模型进行模型检验。

实战解析

原理大概清楚，实践却还是会有诸多问题。下面就通过Python语言贴出主要实现代码。

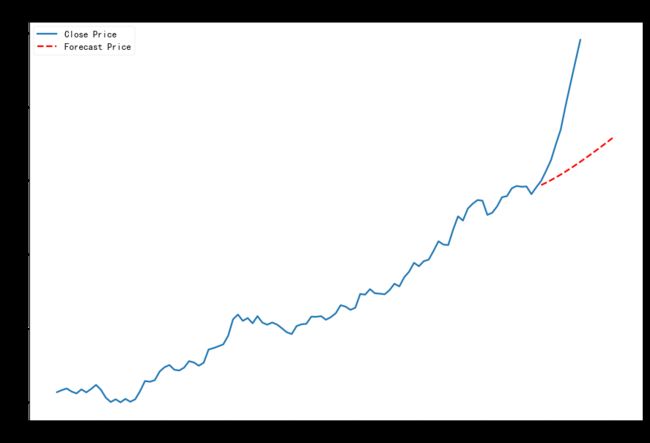
先上最终结果图，红色虚线为预测部分，实线为当前股价，预测趋势向上

# 文中使用到这些基础库：
import tushare as ts 
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima_model import ARIMA
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf

# 获得贵州茅台数据
df_source = ts.get_hist_data('600519')

# 对收盘价进行排序
ser_close = df_source['close'].sort_index()

# 收盘曲线
ser_close.plot(kind='line', c='r', label='Close')

# 20日均线
ser_close.rolling(window=20).mean().plot(kind='line', c='b', ls='--', alpha=.8, label='M_20')

# 趋势不平稳，对数据进行一阶差分
df_close['diff1'] = df_close['close'].diff(1)
# 二阶差分
df_close['diff2'] = df_close['diff1'].diff(1)

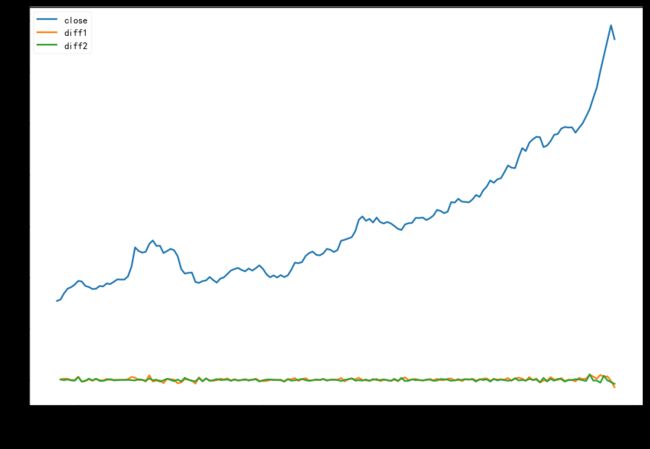
# 日频数据太多，对数据做降频处理
df_close_resample = df_close.resample('W-MON').mean()

# AM与MA定阶，落在置信区间的前一个点位为模型阶数
acf_dif = plot_acf(train_dif1, lags=20)
pacf_dif = plot_pacf(train_dif1, lags=20)

# 把得到的参数放进模型中训练
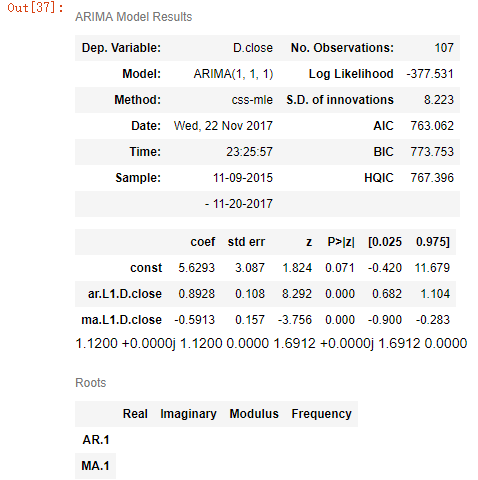
model = ARIMA(stk_train_set['close'], order=(1, 1, 1), freq='W-MON')
arima_result = model.fit()

# 得到预测结果
pred_vals = arima_result.predict(startdate,enddate,dynamic=True, typ='levels')

ARIMA pre result