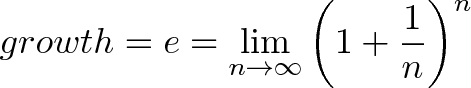在《飞蛾真的是因为趋光所以扑火?》中我们谈到了自然底数e,自然底数e确实是一个神秘数字,这里的e不是一个字母,而是一个数学中的无理常数,约等于2.718281828459。但我总是在想,它到底怎么来的?
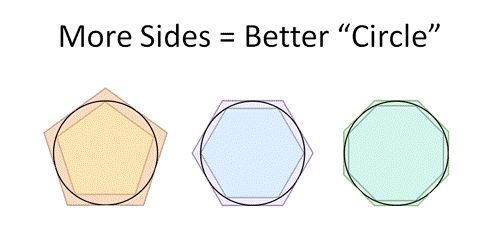
说到e,我们会很自然地想起另一个和它很像的常数π,它们都是常数(拥有确定不变的值),而且都是无理数(也称为无限不循环小数,无法写成两个整数之比) 。π的含义可以通过下图内接与外切多边形来很形象的理解。
假设圆的直径为1,其外切与内接多边形的周长可以构成π的估计值的取值范围上下限,内接与外切多边形的边越多,取值范围就越窄,只要边数足够多,取值范围上下限就可以越来越逼近圆周率π。
那e呢?首先,我们需要知道e这个自然底数的符号是由瑞士数学和物理学家Leonhard Euler(莱昂纳德·欧拉)命名的,取的Euler的首字母“e”。
但实际上,第一个发现这个常数的并而欧拉本人,而是雅可比·伯努利(Jakob Bernoulli)。要了解e的由来,就要谈到一个经济学名称“复利(Compound Interest)”,用俗话说就是所谓的“利滚利”。在引入“复利模型”之前,我们先看看最最基本的 “指数增长模型”。
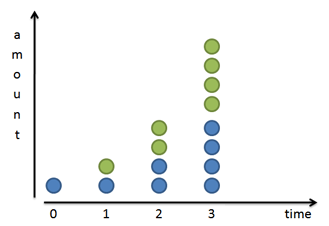
我们知道大部分细菌是通过二分裂进行繁殖的,假设一种细菌1天分裂一次,也就意味着其每一天的数量都是前一天的两倍。
显然,如果经过x次分裂,通俗地说,也就是翻了x倍,那我们得到的总数将是初始数量的2x倍。即:
如果将 “翻倍”换一种更“文艺的”说法,也就是 “增长率为100%”,那我们可以将上式写为:
那么,当我们的增长率不是100%,而是50%、25%之类的,我们只需要将100%换成我们想要的增长率即可,这样就得到了更加普遍的公式:
这个公式的数学内涵是:数量以大小为return的增长率增长,在增长x次之后所得到的总数量为growth。
好了,介绍完指数增长,我们来看看雅可比·伯努利的发现:
从“离散复利”到“连续复利”
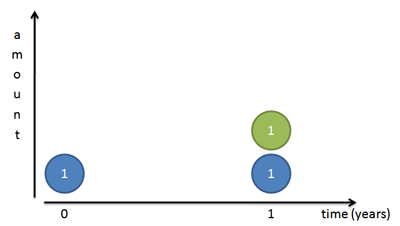
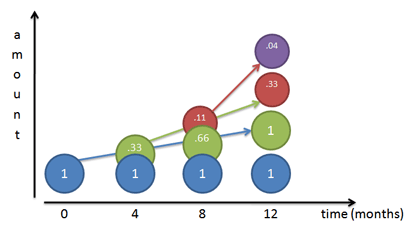
假设你有1元钱存在银行里,而且发生了严重的通货膨胀,银行的利率飙到了100%(就当银行疯了),银行一般一年付一次利息,自然,一年后你可以拿到1元的本金(蓝)和1元的利息(绿),一共两元。
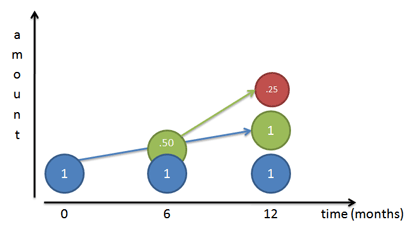
现在银行的年利率不变,但银行为了招揽客户,推出一项惠民政策,每半年就付一次利息。那么到第六个月时,你就能够提前先拿到0.5元的利息。
机智的你会马上把利息提前存入,利息生利息(红),专业术语叫“复利”,那么年底的存款余额将等于2.25元。
此时,我们可以这样看:即银行每半年的利率是50%(或者说100%/2),但一年结算两次。此时我们的计算公式和结果如下:
好,继续,假设现在银行为了和其他银行抢生意,短期不想赚钱了,彻底疯了!每四个月就付一次利息!而机智的你依然一拿到利息就立马存入,与半年付一次利息类似,只不过现在我们可以这样看:即银行每半年的利率是33.33%(或者说100%/3),但一年结算三次。
此时我们的计算公式和结果如下:
我的天,年利率虽然没有变,但随着每年利息交付次数的增加,你年底能从银行拿到的钱也在增加!那么是不是会一直增大到无穷大呢?
想得倒美…
现在假设存款人和银行都疯了,银行在保证年利率为100%的前提下连续不断地付给存款人利息,存款人天天呆在银行不走,拿到利息就往银行里存,感觉耳边响起了:左手右手一个慢动作。
但是,你会发现,似乎有一个“天花板”挡着你疯狂赚钱的小目标,这个“天花板”就是e!
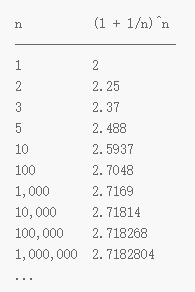
如果,我们进行一系列的运算,不断地提高n的值,我们将看到以下结果:
只要n足够大,结果就会逼近e=2.718281845…
所以,当复利次数趋于无穷大,问题也就从离散复利变成了连续复利,所以我们称其为单位时间增长率为100%的连续复利模型,或者简称“连续复利模型”。对于连续模型,其结果都可以写成与e的表达式:e^rate·time,其中,rate代表利率,time表示时间。当利率为100%,时间为1个单位时间,结果即为e^100%·1=e。因此,e是所有连续增长过程都共有的基本增长率,其“自然”就体现在这儿!
然后,放个大招,高等数学微积分里的一个著名的极限,现在是不是顿时感觉好理解了,而不像高等数学课本中那样感觉就是一个傲娇的公式,总有一种拒人于千里之外的感觉。
好了,也就是说,就算银行的年利率是100%,你再怎么求银行给你“复利”,年底也不可能得到超过本金e倍的余额的。
况且,我是没见过哪个银行的年利率是100%而且还连续复利,还是洗洗睡吧~
Reference:
[1] Leonhard Euler, Wikipedia, http://en.wikipedia.org/wiki/Leonhard_Euler
[2]An Intuitive Guide To Exponential Functions & e,
https://betterexplained.com/articles/an-intuitive-guide-to-exponential-functions-e/
[3] Prehistoric Calculus: Discovering Pi,
https://betterexplained.com/articles/prehistoric-calculus-discovering-pi/
(Sample picture source:betterexplained.com)