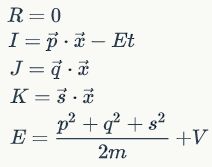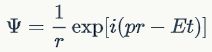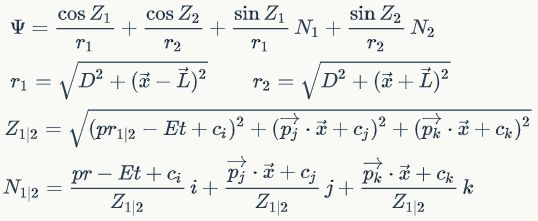如果波函数在四元数体上取值……

让我们开一个脑洞：如果取值为复数的波函数，现在可以在四元数体上取值，那么情况会如何？

首先，波函数依然满足薛定谔方程：

然后，现在波函数和原来量子力学的相比，唯一的区别就是可以取四元数。

为了简单起见，我们做一个简化：

势能V是常值，然后取自然单位制所以薛定谔常数为1。

我们进一步要求此时波函数可以写为如下形式：

代入演化方程可得：

如果我们将J与K这两部分都去掉，那么剩下的当然就是普通的薛定谔方程了。求其自由解，典型的平面波解就为：

我们当然可以参照这一形式来给出自由波函数：

但对于这种波函数的物理解是却存在了问题——

我们现在多了两个静态的标量势，且这两个势能似乎无法通过某些更加基本的第一性原理来获得——它们不是动能，也不知道到底是什么能。

现在我们可以来看球面波。

原本取值为复数时，几率波的自由球面波形式为：

现在，在四元数体上，球面波的形式会变得非常丰富（且荒谬），下面给出一种相对来说最简单的形式：

其中

可见，球对称的情况下，允许存在一些“变化”这的第二、第三复相位所共轭的场，这个场本身可以分解为静态平面波形分布的部分，以及一个球对称且在径向越来越快速震荡的场这么两部分，且这第二、三复相位共轭的场的这第二部分是相互存在耦合的。

我们发现这里总能量除了粒子的动能加势能，还有额外的几项来源，一个就是j和k这两个复方向所共轭的“动量”提供的动能，一个是径向逐渐增大的部分，另一个则存在一定的方向性。

这等于说，如果我们将E依然看作粒子总能量从而必须是守恒的，那么这个系统显然就破坏了这种性质，这样的波函数必然不存在，除非没有这一径向场。

于是，我们下面考虑没有这一第二、三复相位共轭径向场的情况下，球对称波函数的形式：

柱面波的形式与球面波类似。

于是现在考虑双个点源构成的干涉现象：

其中两个N是在三个复单位构成的R3空间中的单位向量。

当不存在第二、三复相位时，两个N当然是相等的，但当存在第二、三复相位的时候它们就不等了，从而可以引发不同的干涉条纹。

其中，最关键的就在于第二、三共轭动量的存在，可能引起干涉条纹的整体偏移等改变。

比如说，当第二、三复相位所关联的常数c非常巨大时，我们发现，系统“退相干”了——这是一个非常有趣的结果。

上述双点源的波干涉结果可以写为：

可见，第二、三复相位的存在的作用便是降低量子相位的“起伏”。

是不是觉得这个Toy Theory很有趣？

由于第二、三复相位现在多了自由度，所以原则上可以得到很多和传统量子理论不同的结果，但有多少是物理上真实的，这个就再说了。

当然了，整个这个模型本就是Toy Theory，和物理也未必有多少关系。

这个模型还可以玩得再“有趣”一点。

比如说，传统的薛定谔方程在标量条件下考虑相对论效应，我们可以得到克莱恩方程：

这个方程相对薛定谔方程来说，最“有趣”的一点在于：没有特别指定的复相位单位i，从而可以得到更加自由的解：

是不是自由度大了很多？

我们还可以做一个适当的变形：

这个的两个方程是不是很眼熟？如果我们将那个任意的复相位单位向量n取为常规的虚数单位i，那么我们实际上得到的（形式上）就是相对论性量子力学中的狄拉克方程！

更有趣的是，四元数的虚数单位之间也恰好满足了Dirac矩阵反对易的特点。

所以，将四元数作为波函数的取值空间，似乎看起来也不是完全没可能哟～～～

当然，这依然只是一个Toy Theory。

---

本文遵守创作共享CC BY-NC-SA 4.0协议

通过本协议，您可以分享并修改本文内容，只要你遵守以下授权条款规定：姓名标示 、非商业性、相同方式分享。
具体内容请查阅上述协议声明。

本文禁止一切纸媒，即印刷于纸张之上的一切组织，包括但不限于转载、摘编的任何应用和衍生。网络平台如需转载必须与本人联系确认。

---

如果喜欢，想要下载App的话，轻戳这里～～
私人推荐订阅专题：《有意思的文章》、《严肃码匠圈》