1.插值函数
%%n次插值多项式
%%X是插值节点,n是插值多项式次数,若已知函数表达式则attribute为0,未知函数表达式但已知函数值时为1
function IPn = Interpolation_polynomials_of_degree_n(X,Y,precision,attribute)
global MAX;global m;global n;global i;
X = sort(X);
[m,n] = size(X);MAX = max([m,n]);error = [];
if attribute == 0
F = ones(1,MAX);
for i = 1:MAX
F(i) = subs(Y,X(i));
end
sum = 0;
for i = 1:MAX
sum = sum+F(i)*Interpolation_basis_fun(X,i-1);
end
IPn = vpa(collect(sum),4);
for i = 1:MAX
error(i) = abs(F(i)-subs(sum,X(i)));
end
%%作图
h=figure;
set(h,'color','w');
t = min(X):(max(X)-min(X))/precision:max(X);
Yreal = subs(Y,t);
T = subs(sum,t);
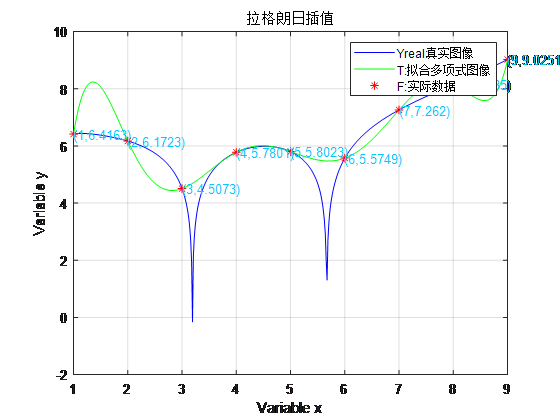
plot(t,Yreal,'b',t,T,'g',X,F,'r*');
grid on
title('拉格朗日插值');
xlabel('Variable x');
ylabel('Variable y');
legend('Yreal:真实图像','T:拟合多项式图像','F:实际数据');
%%显示坐标
for i = 1:MAX
text(X(i),F(i),['(',num2str(X(i)),',',num2str(F(i)),')'],'color',[0.02 0.79 0.99]);
end
disp('误差值为');error
elseif attribute == 1
sum = 0;
for i = 1:MAX
sum = sum+Y(i)*Interpolation_basis_fun(X,i-1);
end
IPn = vpa(collect(sum),4);
h=figure;
set(h,'color','w');
t = min(X):(max(X)-min(X))/precision:max(X);
T = subs(sum,t);
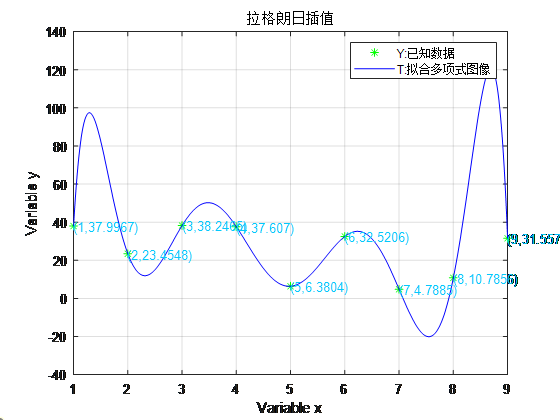
plot(X,Y,'g*',t,T,'b');
grid on
title('拉格朗日插值');
xlabel('Variable x');
ylabel('Variable y');
legend('Y:已知数据','T:拟合多项式图像');
for i = 1:MAX
text(X(i),Y(i),['(',num2str(X(i)),',',num2str(Y(i)),')'],'color',[0.02 0.79 0.99]);
end
end
end
2.插值基函数
%%插值基函数
function IBF = Interpolation_basis_fun(X,k)
[m,n] = size(X);MAX = max([m,n]);
X = sort(X);
mult_x = 1;mult_v = 1;
for i = 1:MAX
syms x;
if i ~= k+1
mult_v = mult_v*(X(k+1)-X(i));
mult_x = mult_x*(x-X(i));
end
end
IBF = mult_x/mult_v;
end
3.插值余项与误差界
%%插值余项与误差限(仅能计算已知的函数表达式下的余项)
function MI = More_than_the_interpolation(X,f,xi,precision)
X = sort(X);
a = min(X);b = max(X);
disp('xi应在以下区间中:');
[a,b]
[m,n] = size(X);MAX = max([m,n]);
Df = diff(f,MAX);Df_value = subs(Df,xi);
MI = vpa(collect(Df_value*omiga(X)/factorial(MAX)),4);
%%误差限
Df_max = max(subs(Df,X));
R_x = vpa(collect(Df_max*abs(omiga(X))/factorial(MAX)),4);
disp('误差上限为:');
R_x
%%作图区
t = a:(b-a)/precision:b;
T1 = subs(R_x,t);
T2 = subs(MI,t);
h=figure;
set(h,'color','w');
plot(t,T1,'r--',t,T2,'g');
grid on
title('误差图像');
xlabel('Variable x');
ylabel('Variable y');
legend('T1:误差上限','T2:指定误差限');
function fac = Factorial(n)
if n == 0
fac = 1;
else
fac = Factorial(n-1)*n;
end
end
end
4.连乘多项式
function ox = omiga(X)
[m,n] = size(X);MAX = max([m,n]);
syms x;
mult = 1;
for i = 1:MAX
mult = mult*(x-X(i));
end
ox=mult;
end
5.例子
clear all
clc
precision=500;
X=1:1:9;
R1=reshape(rand(9),1,9^2);
R2=reshape(rand(18),1,18^2);
R=zeros(1,9);
for i=1:9
R(i)=R1(9*i)*R2(18*i)*100;
end
%%已知函数
disp('已知函数的表达式');
syms x;
f=x*exp(-x^2)+log(abs(exp(x)+precision*sin(x)));
Interpolation_polynomials_of_degree_n(X,f,precision,0)
%%已知函数数值
disp('已知函数值');
Interpolation_polynomials_of_degree_n(X,R,precision,1)
结果
已知函数的表达式
误差值为
error =
0 0 0 0 0 0 0 0 0
ans =
1.621e-5*x^8 + 0.002542*x^7 - 0.1033*x^6 + 1.566*x^5 - 12.15*x^4 + 52.22*x^3 - 122.5*x^2 + 141.6*x - 54.27
已知函数值
ans =
- 0.06151*x^8 + 2.428*x^7 - 40.08*x^6 + 359.3*x^5 - 1899.0*x^4 + 6000.0*x^3 - 10950.0*x^2 + 10420.0*x - 3849.0
图像如下