前两天谈Nassim Nicholas Taleb的遍历性(Ergodicity),那篇译文可能译得太烂不好理解,而近几天得到的万维钢一样在谈Skin in the game一书,今晚也谈了遍历性,他解释得很清楚,这个概念很重要的,不可不听,他解释的部份内容和我早前的另一篇文章「下行风险的秘密」( https://www.facebook.com /notes/yuen-cheng/%E4%B8%8B%E8%A1%8C%E9%A2%A8%E9%9A%AA%E7%9A%84%E7%A7%98%E5%AF%86/ 1244888382310445/ )都有很类近的思想,其实我也说了很多次,不要相信固定合约数的回测,那会误导你相信你的策略或市场是具遍历性,但当有资金大小考虑后就变了一个复杂系统,那是不具遍历性,那些所谓的期望值在真实市场都是没用的东西。
今天是塔勒布《利益攸关》这本书的最后一讲,主题是风险。整个这本书中,塔勒布都在鼓励读者要有点利益攸关,要到真实世界中去冒险,而今天这最后一讲,说的恰恰是要避免重大风险。我们还要讲一个不太容易理解的概念,叫“遍历性”。
1.再论损失厌恶
我们看心理学、行为经济学的书,会经常听到“损失厌恶”这个词。这是一种心理偏误,说人对损失的害怕超过了对获得的喜爱。比如丹尼尔·卡尼曼在《思考,快与慢》里就举了一个非常经典的例子[1]。
咱俩玩一个赌硬币的游戏。如果硬币扔出来是正面朝上,你就要给我100块钱;如果是反面朝上,我给你120块钱。那会有多少人愿意玩这个游戏呢?包括卡尼曼本人、很多研究者都做过类似的实验,结果是大部分受试者都不想玩这个游戏。
硬币正反面朝上的概率都是50%。算概率,这个游戏对你来说是合算的,因为数学期望是你玩一次“平均”净赚10块钱。但是人们就是不愿意玩。
因为大家都觉得损失100块钱有点太多了。研究者就问受试者,你赢了我给你多少钱你才愿意玩?很多人说需要150甚至200块钱。你得把利润率给人提到这么高,别人才愿意冒损失100元的风险。
心理学家认为这是一个偏误(bias),是错误的决策。理性的决策,应该只要数学期望是正的,就坚决选择玩这个游戏。
心理学家这个说法似乎没有毛病。但是塔勒布认为,损失厌恶就算是个偏误,也是一个有道理的偏误。
这就引出了一个重大学术问题。现在有一些学者认为,过去几百年间搞社会科学的这帮人—— 特别是心理学家和经济学家—— 把一个数学问题给搞错了。而这些提出质疑的学者包括塔勒布、包括我们专栏前面讲过的信息论祖师爷香农、包括诺贝尔物理奖得主盖尔曼。
想要理解这一点,我们就必须了解一个不太容易理解的概念。
2.“遍历性”
很多做心理学、社会学研究的人整天跟概率统计打交道,也未必知道这个概念,这就是“遍历性(ergodicity)”。
咱们还是先打比方,塔勒布举了个例子。比如说昨天晚上有100个人去一家赌场赌博,其中99个人赌完了都没事,只有一个人赌到输光了。那请问,这家赌场是不是一个危险的所在?答案似乎是并不危险的,毕竟输光率只有1%。
好。还是这家赌场,我们干脆假定去一次的输光率真的是1%。那请问,如果是同一个人,连续去了这家赌场100次,请问他输光的概率有多大?
答案是他几乎肯定会输光。
这个道理就是空间上—— 也就是同一时间一群人的集合—— 的数学期望,和时间上—— 也就是一个人连续去很多次—— 的数学期望是不一样的。在数学上,这就叫“没有遍历性”。如果空间上和时间上的数学期望相同,就叫“有遍历性”。
2016年,物理学家奥利·彼得斯(Ole Peters)和夸克理论的创始人、诺贝尔物理奖奖得主默里·盖尔曼(Murray Gell-Mann),专门写了一篇论文[2] ,说此前几百年研究社会科学的学者们,都搞错了这个遍历性问题。他们错就错在把集合的概率和时间上的概率给混淆了。
我特意找到了彼得斯和盖尔曼的原始论文。论文有个例子是这样的——
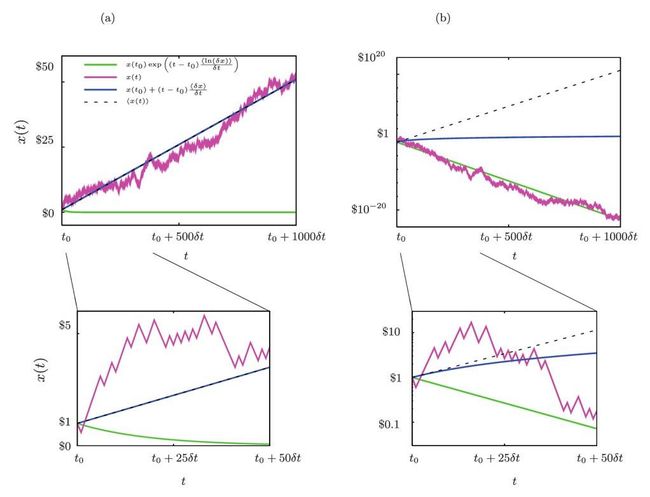
比如现在有个赌硬币的游戏。你投入1元,它50%的可能性会变成0.6元,50%的可能性会变成1.5元,也就是说你或者损失40%或者盈利50%。这么算来,你的数学期望是正的5%,对吧?这跟我们开头说“损失厌恶”时候讲的赌局是一个道理。那么根据心理学家的说法,你应该坚决玩这个游戏,对吧?
先别急。彼得斯和盖尔曼说,这个游戏有两种玩法。
一个玩法是你每次只拿1块钱去玩,假设你有无限多个1块钱,你能够一直玩下去的话,那你长期看来的确是赚钱的。数学期望可以用,你平均每把赢0.05元。这是一个加法的关系。
但是生活中真正的投资,一般不是这么一点一点地玩的。更常见的做法是你把自己所有能动用的资金都押在这个游戏上面,第一把游戏玩完之后,不管结果是多是少,把剩下的钱再次全部押上,这样不断地玩下去。
这种玩法,可就是乘法的关系了。那你最可能的结局是什么呢?是账户清零。
我来帮你算算。比如你玩两把,平均而论你会一赢一输,那么总资产要先乘以0.6再乘以1.5,结果相当于乘以0.9。每玩两把,你平均会赔10%。如果这么一直玩下去的话,玩不了多少把你的资产就清零了。
彼得斯和盖尔曼论文插图。假设遇到的硬币序列是一样的。左边是第一种玩法,财富线性增长;右边是第二种玩法,财富指数清零。
这就是“遍历性”的厉害之处。第一个玩法有遍历性,但是赚钱速度太慢实际生活中没人感兴趣。第二个玩法更实际,但是没有遍历性。对没有遍历性的系统来说,“数学期望”没有太大意义。而历史上那么多研究心理学、决策科学、行为经济学的学者,居然没有考虑到遍历性的问题。
当然也不是所有人都没考虑到。十八世纪的数学家拉普拉斯就已经指出过这个问题,但是学者们没有吸取教训。塔勒布说,香农也考虑过这个问题,而且香农和彼得斯、盖尔曼这些人一样都想对了。这些人为什么能想对呢?因为这些人是天才。
交易员不是天才,但是也想对了,因为交易员有利益攸关。交易员都懂得这个道理,如果你手头的资金确实比较雄厚,那你可以选择风险稍微大一点的投资;但如果你手上的资金并不多,你一定要小心小心再小心,不然你就很可能赔光出局,没有资格再玩了。交易员从来不只看数学期望。心理学家没有利益攸关,反而还觉得交易员都有心理偏误。
这个道理是如果存在赔光的可能,数学期望就没意义。所谓损失厌恶,其实是人们本能地反感这种赌博游戏,这是一种防微杜渐、矫枉过正、勿以恶小而不为的态度,这不叫非理性。
巴菲特有句名言说得好:成功人士和真正的成功人士之间的区别就是,真正的成功人士几乎对所有事情都说不。
谨慎,不是毛病。
3.避免一切尾部风险
遍历性这个概念听着挺复杂,其实说白了也简单。如果你在生活中经常去冒一些可能致命的小风险,而且还是all-in(全压上)—— 比如说高速骑摩托车—— 那就早晚有一天会出事儿。
所以君子不立于危墙之下。很多宗教也好、传统习俗也好、老奶奶的唠叨也好,有各种禁忌,其实说的就是没事儿别作死。
特别是一定要避免所谓“尾部风险”。什么是尾部风险呢?就是在正态分布曲线里面,尾部发生的概率看似很小,但是它对应的后果极其严重,也就是标准的黑天鹅事件。
传统习俗对黑天鹅有非常敏鋭的反感,但是现代一些所谓“理性”的人,却看不到这个危险。
比如说,埃博拉病毒流行的时候,有些记者就说没有必要恐慌,要知道全世界死于埃博拉病毒的人数比美国每年在自己家浴缸中淹死的人都少!这个事实肯定对,但这是不是说埃博拉病毒就不可怕了呢?
塔勒布说,连老奶奶都明白这是两码事。病毒,是“极端斯坦”的事儿,在自己家浴缸里淹死,是“平均斯坦”的事儿。不管世界怎么变化,明年在浴缸里淹死的人数也不会比今年突然增大一倍—— 而病毒就不一样了,如果没有有效的控制,病毒很容易把死亡人数翻倍甚至增加十倍百倍。病毒是有连带效应的东西,它是一个“尾部风险”。
恐怖袭击也是如此。说恐怖袭击不可怕的人,是把恐怖袭击跟车祸相提并论了,是根本就没理解恐怖袭击。
所以塔勒布是个很有意思的人。一方面,他非常赞赏那些冒险的人,他认为人应该冒险、要经历反脆弱,要在风险中成长—— 但这种风险,主要是“波动性”,是不致命的。而另一方面,他强烈反对冒黑天鹅式的风险。
| 由此得到
今天如果你只想记住一个简单的道理,那就是如果这件事存在一个尾部风险,哪怕这个风险很小,你也应该避免去做。这个道理连老奶奶都知道,可是有些专家不知道。
而如果你想变复杂,那就应该仔细琢磨一下“遍历性”这个概念。这是一个很重要的思想,有很多搞了一辈子社会科学的学者都不知道它。理解这个道理,能让你做出更准确、更复杂的决策。本周五我还会专门再讲讲这个数学原理。
至此《利益攸关》这本书就给你讲完了。我们跟着塔勒布探讨了一番道理,演练了一点数学,最酷的是还颠覆了象皮凯蒂、平克、道金斯、卡尼曼这些牛人的思想和道德、雇员、黄金大米、损失厌恶这些概念,至于什么鲁宾、戈尔、扎克伯格这些所谓名人,更是不在话下。
读书人不能像个追星族一样整天仰望世界,你得变成俯视视角,才是真的钻研学问。我说过读塔勒布能让你充满底气,我们做到了。
参考文献
[1] 我们专栏以前讲“标准差”的时候说过类似的例子,那是另一个视角和主题。
[2] O. Peters and M. Gell-Mann, Evaluating gambles using dynamics, Chaos 26, 023103 (2016); https://aip.scitation.org/doi/full/10.1063/1.4940236
来源:得到:万维钢精英日课