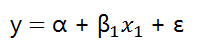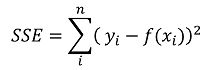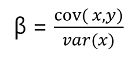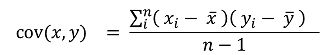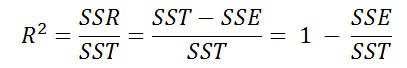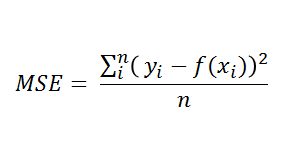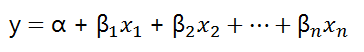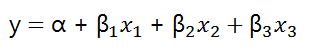摘要:本文结合实际案例,介绍机器学习的线性回归模型,包括一元线性回归和多元线性回归,以及模型的评估。案例展示用Python代码实现。
一元线性回归
在机器学习系列1——机器学习概况中我们讲到,监督学习的主要任务是做预测,其中一种是回归性预测,预测某一个连续型变量的数值。在线性回归模型中,根据输入变量的个数(即特征值个数),可以将模型分为一元线性回归模型和多元线性回归模型。我们先讲解一元线性回归。
如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。
一元线性回归模型的表示:
这里
的ε表示误差项,也叫随机干扰项,即真实值和预测值之间的差异。
在线性回归模型中,有六大假设:
- 对模型设定的假设:
【假设1】回归模型是正确设定的,即模型选择了正确的变量,且选择了正确的函数形式。 - 对解释变量的假设:
【假设2】解释变量x是确定性变量,不是随机性变量,在随机抽样中取固定值。
【假设3】解释变量X在所抽取的样本中具有变异性,而且随着样本容量的无限增加,解释变量X的样本方差趋于一个非零的有限常数。样本方差的极限为非零的有限常数的假设,则旨在排除时间序列数据出现持续上升或下降的变量作为解释变量,因为这类数据不仅使大样本统计推断变得无效,而且往往产生所谓的伪回归问题(spurious regression problem)。 - 对误差项ε的假设:
【假设4】误差项ε是一个期望为0的随机变量。
【假设5】误差项ε与解释变量之间不相关,即两者协方差为0。
【假设6】误差项ε是一个服从正态分布的随机变量,且相互独立。
案例
假设我们有以下汽车相关的数据(仅以前两行示例)。
| 燃油 | 气缸 | 排量 | 马力 | 重量 | 加速度 | 型号年份 | 原产地 |
|---|---|---|---|---|---|---|---|
| mpg | cylinders | displacement | horsepower | weight | acceleration | model_year | origin |
| 18.0 | 8 | 307.0 | 130.0 | 3504.0 | 12.0 | 70 | 1 |
| 15.0 | 8 | 350.0 | 165.0 | 3693.0 | 11.5 | 70 | 1 |
数据集下载: https://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/
其中:
mpg - 燃油效率
model_year - 型号年份,70代表1970年
origin - 原产地,0:北美;1:欧洲;2:亚洲
我们想知道,汽车的气缸、排量、马力、重量、加速度、型号年份、原产地等这些特征,对汽车的燃油效率有什么影响,从而判断可以根据哪些特征,预测出燃油效率。
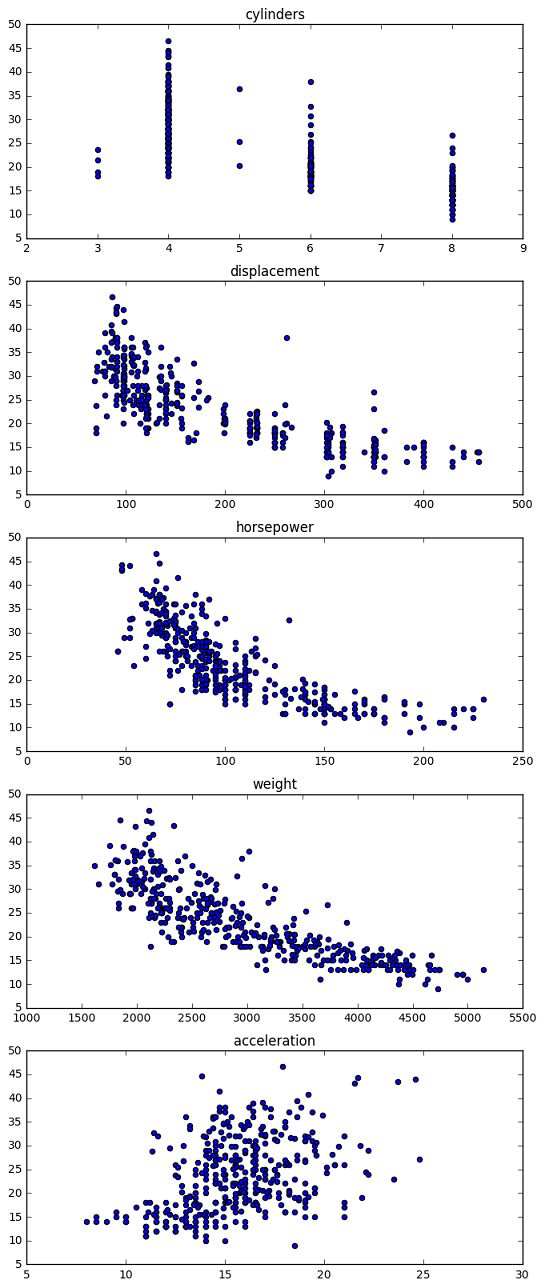
我们可以先探索一下,这些特征分别和燃油效率的相关度有多大。
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
cars = pd.read_table('auto-mpg.data', delim_whitespace = True)
#删除horsepower值为'?'的行
cars = cars[cars.horsepower != '?']
#用散点图分别展示气缸、排量、马力、重量、加速度与燃油效率的关系
fig = plt.figure(figsize = (8,20))
ax1 = fig.add_subplot(5,1,1)
ax2 = fig.add_subplot(5,1,2)
ax3 = fig.add_subplot(5,1,3)
ax4 = fig.add_subplot(5,1,4)
ax5 = fig.add_subplot(5,1,5)
ax1.scatter(cars[['cylinders']], cars['mpg'], label='a')
ax1.set_title('cylinders')
ax2.scatter(cars[['displacement']], cars['mpg'])
ax2.set_title('displacement')
ax3.scatter(cars[['horsepower']], cars['mpg'])
ax3.set_title('horsepower')
ax4.scatter(cars[['weight']], cars['mpg'])
ax4.set_title('weight')
ax5.scatter(cars[['acceleration']], cars['mpg'])
ax5.set_title('acceleration')
plt.show()
可以看出,重量Weight、马力Horsepower、排量Displacement和燃油效率呈现明显的相关性。为了说明一元线性回归,这里我们先假设,重量Weight和燃油效率的关系最大,我们采用重量Weight来预测燃油效率。
为了预测,我们需要找到一个模型,能够很好的描述重量和燃油效率之间的关系,这个过程叫做拟合。我们用一元线性回归方程y=α+βx来表示他们之间的关系,其中y表示输出变量,这里是燃油效率,x为输入变量,这里是重量,α为截距,β为相关系数,这两个参数是我们最关心的。因为重量和燃油效率之间为负相关,这里β应该是一个负数。
我们利用Python中的 Scikit-learn中的LinearRegression来构建一元线性回归模型。Scikit-learn是建立在Python的NumPy和matplotlib库基础之上机器学习库,支持的机器学习算法包括分类,回归,降维和聚类,还有一些特征提取(extracting features)、数据处理(processing data)和模型评估(evaluating models)的模块。
from sklearn.linear_model import LinearRegression
#sklearn中的模型是面向对象的,使用之前需要初始化模型
lr_model = LinearRegression()
#拟合模型
lr_model.fit(cars[['weight']], cars['mpg'])
#预测
cars['predictions'] = lr_model.predict(cars[['weight']])
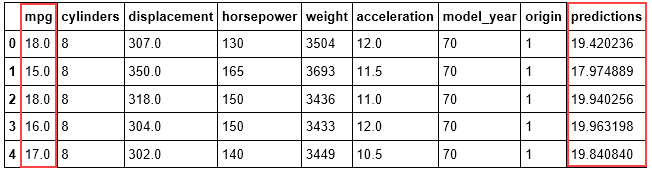
#显示
cars.head(5)
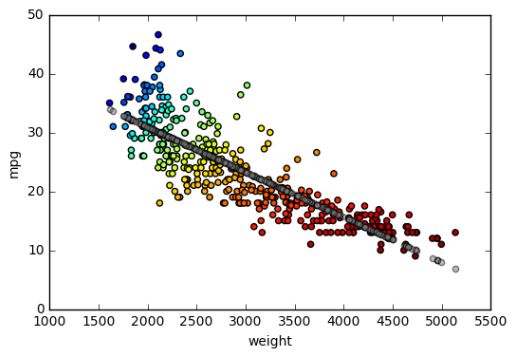
现在原燃油效率、预测的燃油效率和重量的关系如下:
import numpy as np
#设置散点颜色
T = np.arctan2(cars['weight'],cars['mpg'])
plt.scatter(cars['weight'], cars['mpg'], c = T)
#alpha为设置透明度
plt.scatter(cars['weight'], cars['predictions'], c = 'grey', alpha = 0.5)
plt.show()
可以看出来,预测的燃油效率和重量的关系,呈现出一元线性回归方程y=α+βx的模式,即一条直线。参数α和β的估计,一般是通过最小二乘法确定的,其基本思想是使所有点到这条直线的距离的平方和最小。这里的距离也叫残差(residual)或者训练误差(training errors),所以训练模型的过程,也是寻找最小残差平方和(SSE,Sum of Squares for Error,经济学相关领域也把这个叫做Residual Sum of Squares,两者是同一个概念)的过程。
其中yi是观测值,f(xi)是预测值。
相关系数β的计算方式为:
这里cov(x,y)为x和y的协方差,var(x)为x的方差。协方差是x和y总体误差的期望值,用来衡量x和y的总体误差,如果x和y的变化趋势一致,则协方差为正值,反之为负值,如果协方差为0,表明x和y不相关。而方差是协方差的一种特殊情况,即x和y是同一个变量的情况,方差衡量了样本值的离散程度,即样本值和样本均值的偏离程度,方差越高,样本值越离散,方差越低,样本值越集中。
方差计算方式为(注意这里为样本方差,自由度为n-1,不同于总体方差,自由度为n):
协方差计算方式为:
在Python中计算方差和协方差:
#计算方差
var = cars['weight'].var()
#计算协方差
cov = cars[['weight','mpg']].cov().iloc[0][1]
计算所得方差var(x) = 721484.7090075163,协方差cov(x,y) = -5517.44070411。
由此可得相关系数 β = cov(x,y) / var(x) = -0.00764734253578。
得到 β 之后,α 就可以通过以下方式计算出来:
α = 46.216524549017578
这样我们就得到了该模型的一元线性回归方程: y = 46.22 - 0.008*x
带入任何重量值x,都可以预测出相应的燃油效率y。
模型评估
得到模型参数之后,我们如何评价模型在现实中的表现呢?因为回归直线只是一个近似拟合,有很多点没有落在直线上,那我们如何判定,回归直线的拟合程度?
R^2 (Coefficient of Determination)
一般常用的判定指标是R^2 (coefficient of determination),又叫判定系数、拟合优度,确定系数,或者决定系数。一元线性回归中的R^2是皮尔逊积矩相关系数(Pearson product moment correlation coefficient或Pearson's r)的平方。
其中:
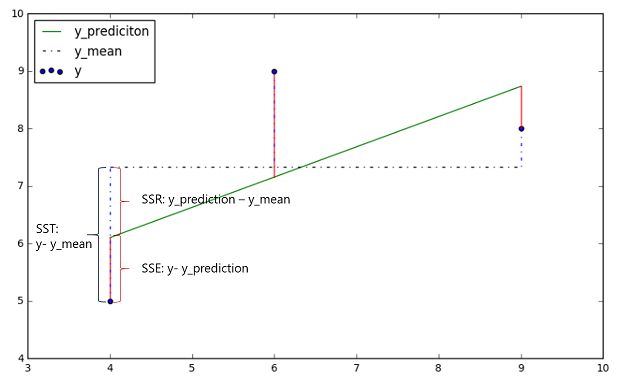
- SST(Sum of Squares for Total):总偏差平方和是每个实际值y和其总体平均值之差的平方和,描述的是总体的波动情况。例如在上面的实例中,燃油效率是随着重量和其他特征而上下波动的。
- SSR(Sum of Squares for Regression):回归平方和是每个y对应的预测值f(x)和y的总体平均值之差的平方和,反映了y的总偏差中,由于x和y的线性关系引起的y的变化部分,可以由回归直线来解释。例如上面实例中,重量对燃油效率的影响,就是通过回归直线来解释的。
- SSE(Sum of Squares for Error):残差平方和描述的是,除了x对y的线性影响之外的其他因素对y变化的作用,是不能由回归直线来解释的。例如上面实例中,我们只是假设重量对燃油效率有影响,但实际上马力、加速度等特征和燃油效率之间也呈现明显的相关性,对燃油效率也有影响,而这些特征对燃油效率的影响,是不能通过我们拟合的“重量和燃油效率的线性回归直线”来解释的。
所以,SST(总偏差)=SSR(回归线可以解释的偏差)+SSE(回归线不能解释的偏差)
如下图所示,3个蓝色点为训练集样本x和y之间的关系,绿色直线为拟合出来的回归线,水平黑色虚线代表了样本中y的平均值。SST描述的是每个样本y值和它自己的均值之间的差异关系;SSR描述的是y的预测值(拟合出来的回归线上的值)和样本y的均值之间的差异关系;SSE描述的是每个样本y值和y的预测值之间的差异关系。
R^2 = 1 - SSE/SST,取值介于0和1之间,越接近1,说明拟合程度越高。如果SSE为0,代表所有点都落到拟合的直线上,则R^2 = 1,说明回归直线能够完全描述样本中x和y的线性关系,y的变化只受x的影响,没有其他影响因素。反之如果SSE很大,R^2值接近于0,则说明拟合直线不能很好的解释x和y的关系,x和y之间可能不存在线性关系。
Python中可以直接用sklearn.metrics中的r2_score函数计算R^2 值,LinearRegression中也提供了直接计算R^2 的函数score:
#用sklearn.metrics中的r2_score函数计算
from sklearn.metrics import r2_score
r2_score = r2_score(cars['mpg'],cars['predictions'])
#用LinearRegression中的score函数计算
score = lr_model.score(cars[['weight']],cars['mpg'])
计算所得r2_score = score = 0.69,说明拟合程度还可以,样本中超过一半的数据可以用回归直线来解释,但不是很理想。
均方误差MSE(Mean Squared Error)
我们可以用均方误差(Mean Squared Error)来衡量模型的误差。均方误差的定义为:
有没有发现,这个其实就是残差平方和的平均值。
Scikit-learn中提供了直接计算均方误差的函数:
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(cars['mpg'], cars['predictions'])
计算所得mse = 18.68。
但是MSE存在一个问题,它是平方和的均值,与样本不是同一个量纲,也就是误差是被平方扩大了的误差。
所以常用的是MSE的平方根RMSE(Root Mean Square Error)。
多元线性回归
用【重量】预测【燃油效率】的效果并不显著(R^2 = 0.69)。那么如何改进预测效果呢?
我们看到,其实除了【重量】之外,其他特征值比如【马力】和【排量】和【燃油效率】也呈现明显的负相关性。就是说,【燃油效率】除了受【重量】影响之外,也很可能受【马力】和【排量】影响。为了更好的预测燃油效率,我们需要增加这些特征作为输入变量,一元线性回归模型已经无法满足我们的要求了,所以我们要用更具有一般性的模型来表示,即多元线性回归模型。
假设我们增加【马力】和【排量】两个输入变量,那么我们的模型应该是:
x1表示【重量】,x2表示【马力】,x3表示【排量】。
我们用Python重新预测【燃油效率】:
#初始化模型
mul_lr_model = LinearRegression()
#拟合模型
mul_lr_model.fit(cars[['weight','horsepower','displacement']], cars['mpg'])
#预测
cars['predictions_mul'] = mul_lr_model.predict(cars[['weight','horsepower','displacement']])
#显示
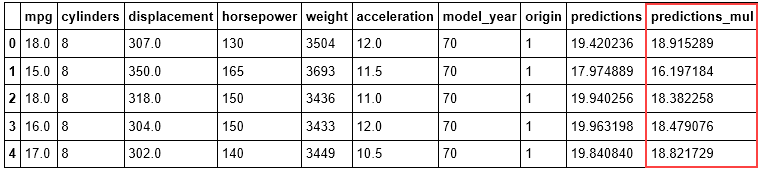
cars.head(5)
直观上来看,多元回归的结果prediction_mul数值上更接近原【燃油效率】mpg。我们来计算一下多元回归的R^2。
mul_score = mul_lr_model.score(cars[['weight','horsepower','displacement']], cars['mpg'])
所得mul_score = 0.71,比一元回归的score = 0.69更好一点。
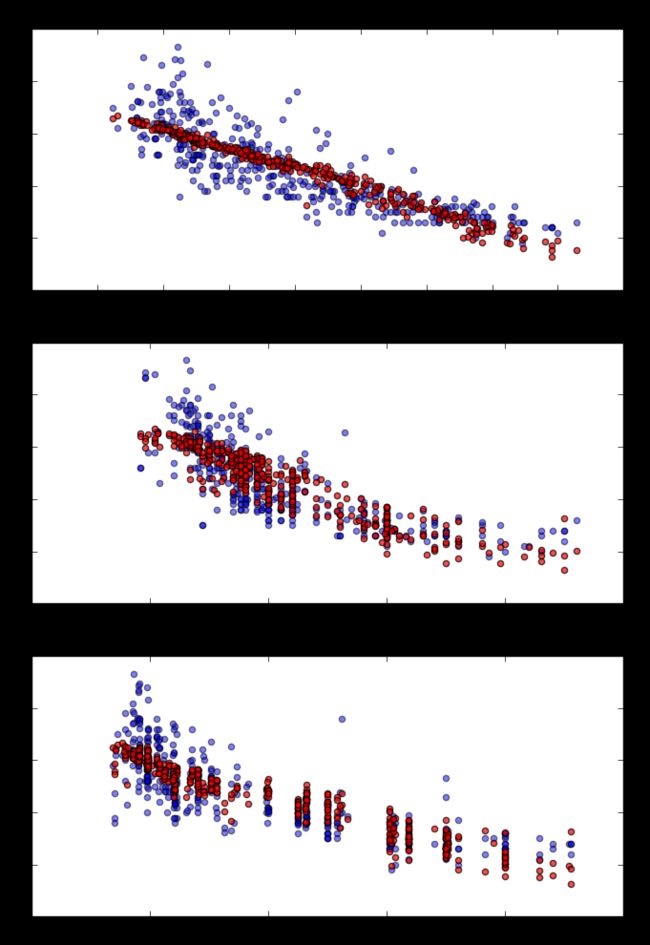
我们通过散点图来看一下多元回归模型的预测值和各个特征值之间的关系:
fig = plt.figure(figsize = (8,12))
ax1 = fig.add_subplot(3,1,1)
ax2 = fig.add_subplot(3,1,2)
ax3 = fig.add_subplot(3,1,3)
ax1.scatter(cars[['weight']], cars['mpg'], c='blue', alpha=0.5)
ax1.scatter(cars[['weight']], cars['predictions_mul'], c='red', alpha=0.7)
ax1.set_title('weight')
ax2.scatter(cars[['horsepower']], cars['mpg'], c='blue', alpha=0.5)
ax2.scatter(cars[['horsepower']], cars['predictions_mul'], c='red', alpha=0.7)
ax2.set_title('horsepower')
ax3.scatter(cars[['displacement']], cars['mpg'], c='blue', alpha=0.5)
ax3.scatter(cars[['displacement']], cars['predictions_mul'], c='red', alpha=0.7)
ax3.set_title('displacement')
plt.show()