背景介绍
数据集包含欧洲持卡人于2013年9月通过信用卡进行的交易。这个数据集显示了两天内发生的交易,在284,807笔交易中我们有492笔诈骗。
数据集非常不平衡,正面类(欺诈)占所有交易的0.172%。
数据集只包含数值输入变量,这是PCA变换的结果。不幸的是,由于保密问题,我们无法提供有关数据的原始特征和更多背景信息。特征V1,V2,... V28是使用PCA获得的主要组件,没有用PCA转换的特征是“时间”和“金额”。“时间”包含数据集中每个事务和第一个事务之间经过的秒数。“金额”是交易额,此特征可用于基于样本的成本灵敏度学习。特征'类'是响应变量,如果发生欺诈,则取值1,否则为0。
初步分析
我们的目的是通过训练得到一个模型,这个模型通过特征变量能识别出该笔交易是否发生欺诈。
由背景介绍可知:
- 正反样本分布极度不平衡,可能对预测存在影响,需要衡量采用过采样还是下采样来解决这个问题。
- 数据集已经过PCA变换,相对干净,可以将重点放在建模分析上。
- 一般评价模型我们用的准确度,但是结合实际业务,在准确度很高的情况下可能FN很高但是TP很低,翻译一下就是欺诈识别能力不怎么样,这不符合我们的预期。我们希望考察模型的欺诈识别能力,同时也兼顾模型的准确度,所以我们考虑用Recall指标:TP/(TP+FN)
数据预处理
由于数据已相对干净,这里我们着重考虑样本平衡问题。
首先还是处理一下“amount”变量,做一个变换让变量值落在[-1,1]的区间内。
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.preprocessing import StandardScaler
data = pd.read_csv("creditcard.csv")
data['normAmount'] = StandardScaler().fit_transform(data['Amount'].reshape(-1, 1))
data = data.drop(['Time','Amount'],axis=1)
现在我们考虑样本平衡问题,要让样本平衡很容易想到的一个方法就是反面样本集中抽取和正面样本集数量一致的样本形成新的反面样本集,也就是所谓的下采样方法。
number_records_fraud = len(data[data.Class == 1])#欺诈样本数量
fraud_indices = np.array(data[data.Class == 1].index)#欺诈样本索引
normal_indices = data[data.Class == 0].index#正常样本索引
random_normal_indices = np.random.choice(normal_indices, number_records_fraud, replace = False)#从正常样本中采样,第二个参数表示采样数量
random_normal_indices = np.array(random_normal_indices)
under_sample_indices = np.concatenate([fraud_indices,random_normal_indices])#合并正常样本和欺诈样本形成新的数据集索引
# 根据索引形成下采样数据集
under_sample_data = data.iloc[under_sample_indices,:]
print(u"正常样本比例: ", len(under_sample_data[under_sample_data.Class == 0])/len(under_sample_data))
print(u"欺诈样本比例: ", len(under_sample_data[under_sample_data.Class == 1])/len(under_sample_data))
print(u"下采样总样本数: ", len(under_sample_data))
#正常样本比例: 0.5
#欺诈样本比例: 0.5
#总样本数: 984
下采样已经完成,可以切分数据集准备建模了。
X_undersample = under_sample_data.loc[:, under_sample_data.columns != 'Class']
y_undersample = under_sample_data.loc[:, under_sample_data.columns == 'Class']
X_train_undersample, X_test_undersample, y_train_undersample, y_test_undersample = train_test_split(X_undersample,y_undersample ,test_size = 0.3 ,random_state = 0)
建模分析
分类算法我们先考虑业界的流行算法——逻辑回归。
确定特征、确定模型之后,我们还需要考虑的就是模型的参数。利用交叉验证法我们来选一下逻辑回归的正则化惩罚力度参数。
#逻辑回归的参数选择
def printing_Kfold_scores(x_train_data,y_train_data):
fold = KFold(5,shuffle=False)
# 待选参数数组
c_param_range = [0.01,0.1,1,10,100]
results = pd.DataFrame(index = range(len(c_param_range),1), columns = ['C_parameter','Mean recall score'])
results['C_parameter'] = c_param_range
# k-fold 后, indices[0]作为训练集, indices[1]作为测试集
j = 0
for c_param in c_param_range:
print('-------------------------------------------')
print('C parameter: ', c_param)
print('-------------------------------------------')
print('')
recall_accs = []
for iteration, indices in enumerate(fold.split(x_train_data,y_train_data),start=1):
lr = LogisticRegression(C = c_param, penalty = 'l1')
lr.fit(x_train_data.iloc[indices[0],:],y_train_data.iloc[indices[0],:].values.ravel())
y_pred_undersample = lr.predict(x_train_data.iloc[indices[1],:].values)
#计算recall值
recall_acc = recall_score(y_train_data.iloc[indices[1],:].values,y_pred_undersample)
recall_accs.append(recall_acc)
print('Iteration ', iteration,': recall score = ', recall_acc)
# The mean value of those recall scores is the metric we want to save and get hold of.
results_table.ix[j,'Mean recall score'] = np.mean(recall_accs)
j += 1
print('')
print('Mean recall score ', np.mean(recall_accs))
print('')
#选出分数最高的参数C
best_c = results_table.loc[results_table['Mean recall score'].idxmax()]['C_parameter']
# Finally, we can check which C parameter is the best amongst the chosen.
print('*********************************************************************************')
print('Best model to choose from cross validation is with C parameter = ', best_c)
print('*********************************************************************************')
return best_c
这组参数中c=0.01时表现最好,下采样测试集上的recall为 0.938775510204,暂取c=0.01。(PS:0.01不是最佳参数,只是这一组中表现最好的)
看看模型在整个测试集上的表现。
import itertools
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.3, random_state = 0)
#建模预测
lr = LogisticRegression(C = best_c, penalty = 'l1')
lr.fit(X_train,y_train.values.ravel())
y_pred= lr.predict(X_test.values)
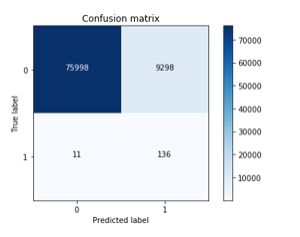
#混肴矩阵
cnf_matrix = confusion_matrix(y_test,y_pred)
np.set_printoptions(precision=2)
print("基于测试集的Recall: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# 图形化
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
, classes=class_names
, title='Confusion matrix')
plt.show()
recall为0.925170068027,表现良好。
所谓没有对比就没有伤害,我们来看看没有经过下采样处理的情况。
将输入改成整个数据集,再做一次参数选择。
best_c = printing_Kfold_scores(X_train,y_train)
这回选的是10,且recall为0.61847902217。
结果说明下采样处理能够显著提高欺诈识别能力。
过采样
上文提到除了下采样我们还可以采用过采样,也就是我们构造数据使欺诈样本和正常样本保持平衡。
这里我们采用过采样中的经典算法SMOTE。
oversampler=SMOTE(random_state=0)
X_oversample,y_oversample=oversampler.fit_sample(X_train,y_train)
X_oversample = pd.DataFrame(X_oversample)
y_oversample = pd.DataFrame(y_oversample)
best_c = printing_Kfold_scores(X_oversample,y_oversample)
lr = LogisticRegression(C = best_c, penalty = 'l1')
lr.fit(X_oversample,y_oversample.values.ravel())
y_pred = lr.predict(X_test.values)
cnf_matrix = confusion_matrix(y_test,y_pred)
np.set_printoptions(precision=2)
print("基于测试集的Recall: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
, classes=class_names
, title='Confusion matrix')
plt.show()
c选择100,recall为0.918367346939。
小结
对比下采样和过采样,两者的recall指标相差不远,但是下采样的误杀率明显高于过采样,因此在处理样本不平衡问题时,SMOTE是被广泛采用用的手段之一。
综上,在解决欺诈检测类问题时,样本不平衡问题可能是我们无法避免的问题,一方面欺诈本就属于不常见样本,缺乏历史数据,和安全类软件的病毒检测处于类似的境地;另一方面,参考安全问题,我们目前解决的还是根据历史经验解决欺诈问题,面对越来越复杂的环境,我们可能需要更多的预防手段,仅仅依赖历史数据可能还不够。