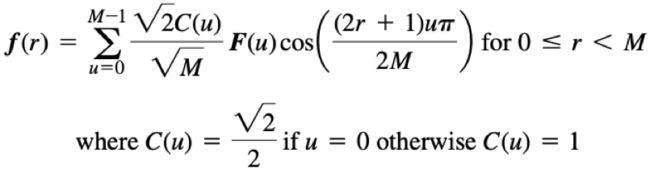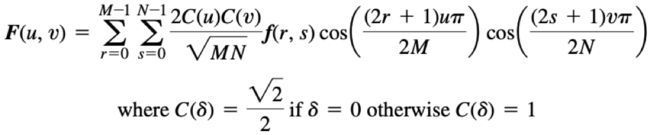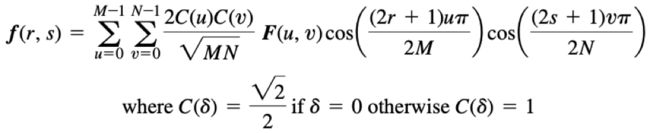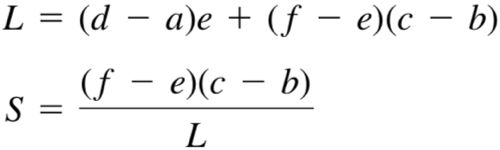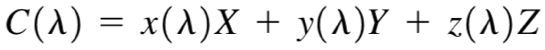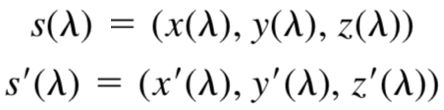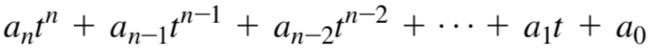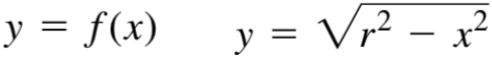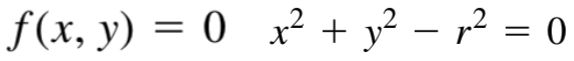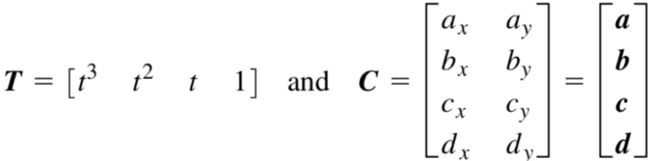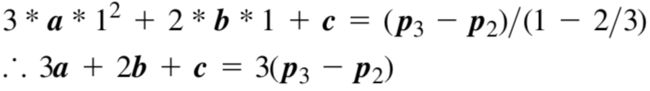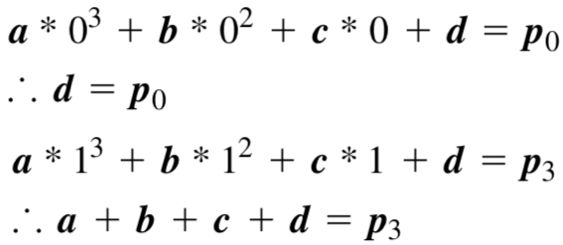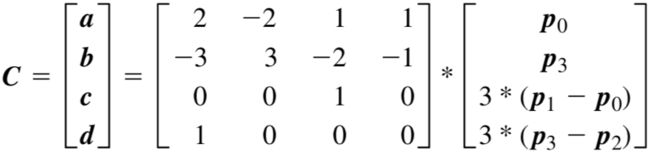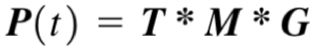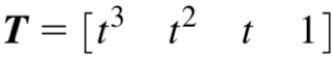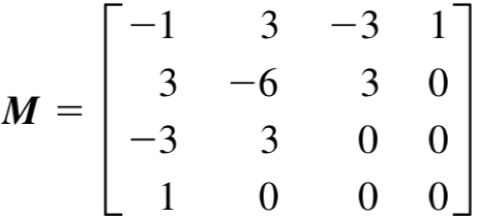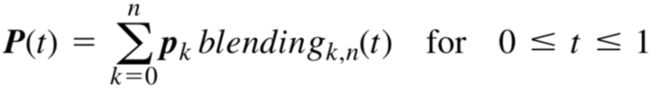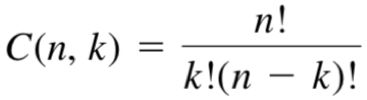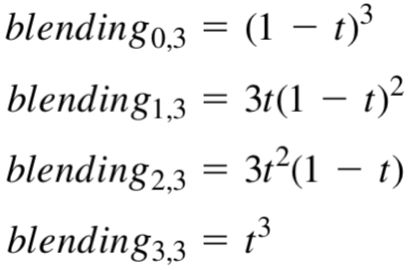1 简介
本文在The Science of Digital Media的基础上对数字图像的采集、颜色模型等理论基础知识进行了概括和总结。其中主要包括了位图和矢量图的采集,图像空间频率,二维离散余弦变换,颜色学基础,贝塞尔曲线和算法艺术的相关介绍。
数字图像的类型可以划分为位图、矢量图,以及算法和程序后建模三类图像。其中位图图像又称像素图或者光栅图像,这种图像是通过逐像素的指定每个像素点的颜色创建。矢量图像通过使用对象定义和数学方程来描述颜色和形状创建。程序后建模图像也称算法艺术,它通过结合数学、逻辑性、控制结构以及递归来决定每个像素点的颜色。
2 位图
2.1 创建位图
位图的创建方式可以是通过Photo Shop等绘图软件绘制,使用扫描仪扫描模拟图像,或者使用数码相机拍摄。这里关注使用数码相机拍摄得到的位图。
数码相机创建位图的过程可以分为采样、和量化两个阶段。采样指的是从连续的模拟图像中提取离散像素点的过程。有些设备允许用户设置拍照或者录制视频时的采样率,即采样时横向和纵向维度上采集的像素点数量。如在iOS12系统的iPhone手机中,在设置界面可以设置视频录制的采样率。
量化是指定颜色模型和对应位深度,并使用实际的数值来表示像素颜色的过程。一张经过合理采样及量化的图如下。
采样和量化的过程都会引入误差。即得到的图像并不是我们所观测到的原始图像。如果在采样的过程中使用的采样率过低会导致图片丢失大量的细节。在其显示的大小和原图一致时我们将会看到大量如马赛克效果一样的色斑,如下图。
同样的,如果在量化过程中设置了过低的位深度,那么会导致得到的图片能够表示的颜色数量十分有限。也就是一些相近的颜色被表示成了同一个颜色,图片同样会损失大量细节,如下图。
2.2 像素尺寸、分辨率和图像大小
我们描述一张照片尺寸时通常使用像素点在宽和高方向上的数量来表述,而对于计算机屏幕而言,像素的数量和屏幕上具体的亮点的数量相关。因此为了明确区分这两种不同的语境,在描述图片尺寸时我们使用术语逻辑像素,在描述计算机屏幕时我们使用术语物理像素。
生活中的广告通常会描述某个手机的相机高达几百万像素,这是指的该设备能够支持的最大像素尺寸。如其硬件能够生产的图像最大逻辑像素为2048*1536,即该设备可生成的最大图像包含3 145 728个像素,即300万像素。需要注意的是,有些相机制造商会使用“数码变焦”的方式来夸大其相机性能,这种软件方式能够增加图片的像素但是不能真正提高清晰度。
分辨率定义为图像文件某个维度在每英寸空间中的像素数量,其单位为ppi。如200ppi。打印分辨率是指打印机在每英寸空间内能够打印的最大点数量,其单位为dpi,如1440dpi。
图像的大小定义为图像文件被打印出来或者在计算机屏幕上的物理尺寸。单位是英寸或者厘米。
改变图像的像素尺寸称为重采样。通过放大增加图像的像素尺寸称为上采样,通过缩小减少像素尺寸称为下采样。上采样的像素只是根据原有像素进行的插值计算,下采样的像素值是已有像素值的平均,它们都不能提高图像的清晰度。
2.3 数字图像的空间频率
在本系列文章的数字数据中已经介绍过数据能够使用函数表示,并且可以从一个域变换到另外一个域而不丢失信息。数字图像也能适用这个规律,同样在数字图像中尼奎斯特定理仍然适用。
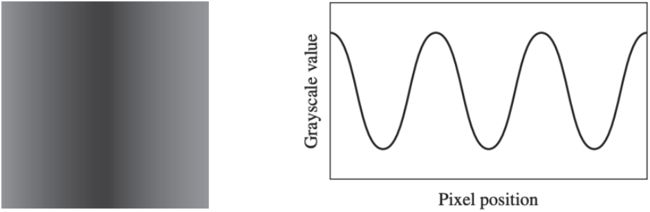
对于上图中左侧灰度图像,想定和x轴平行的一条直线,将其灰度值表示为y,将其像素点点位置表示为x,就可以得到右边的波形图。对于带有RGB通道的彩色图像,只需要对其三个通道做相同的处理即可。在右图中我们假定左侧灰度图周期重复,这样便得到的周期重复的波形图。
在处理数字图像时,我们得到的是离散化的数据,如上面的左图。我们同样可以通过重复周期信号得到周期的波形图,如上面右图。
实际上,在处理真实的数字照片时也能够将图片分离出RGB3个通道,分别处理每个通道的图片。这里为了简单颜色,我们将图片处理成灰度图,如上面左图。我们在其中选择某一行像素,利用和前面相同的手法绘制出其波形图,如上面右图。可以看出,我们能够使用二维波形去描述一张数字图片的某行像素。
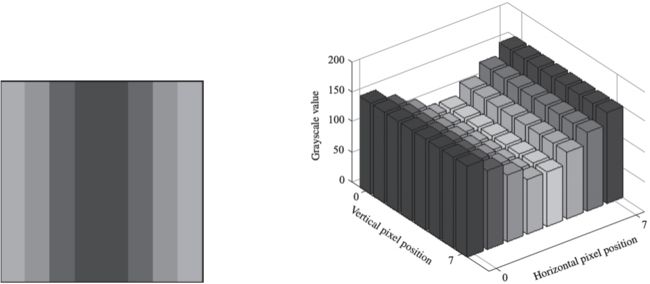
前面已经讲到可以使用二维波形去描述一张数字图片的某行像素,但是这还不够。图片具有二维的特征,因此我们还必须找到一种方法同时描述像素点在x轴和y轴上的变化。空间波形能够很好的实现这个目标,如上面左图为一张灰度图,通过在3维空间中将其像素点的位置映射到x轴和y轴,将其实际的灰度值映射到z轴,我们便能够得到一个3维的空间波形图,即上面右图。
对于一张实际的数字图像,这里仍然使用小鸟图作为例子,我们仅考虑其灰度图像。对于带有RGB通道的彩色图像而言,只需分离RGB三个颜色通道做类似的处理即可。上面左图为实际的数字图像,经过转换后的空间波形如右图。可以看出,我们可以使用空间波形图的方式去描述任何一张数字图像。这点十分重要,因为只有当能够使用物理模型去描述数字图像时,我们才方便对其进一步处理。而通过空间波描述,我们才能将其转换为空间频率,这是图像有损压缩的数学基础。
3 离散余弦变换
在本系列文章的第一篇文章中已经对傅立叶级数以及其推倒出的各种傅立叶变换做了介绍,并且进行详细的推导。前面已经说过,任何复合狄利克雷条件的周期函数都能够被分解为无穷多个简单的正弦函数。在公式中我们长看到有余弦分量,这是由于正弦函数Asin(ωx+φ) 使用三角公式展开后可以得到余弦值。而离散余弦变换又是在某些条件下将正弦项约分后的结果。具体介绍请看该系列的第一篇文章《数字信号的表示和处理》。
上图是离散余弦变换的示意图,再次强调这里只是示意图。最右侧的波形图可以通过左侧的3个基础波形图合成。对于更复杂的波形,仍能将其转换为多个简单波形的组合。这个结合数字图像的主题可以理解为单行像素的波形图可以呗转换为多个基础波形的组合。
上面是离散余弦逆变换的公式,其中f[u]为原始信号在频域的函数,M为原始信号的个数。这是一维的离散余弦变换公式,实际上在进行数字图像处理时需要用到的是二维的离散余弦变换公式,这个会在本篇文章的后面部分介绍。我们首先关注1维的离散余弦变换,并借助它颜色图像中的一行像素如何被分割为多个波形的组合。
假定有一个数字图像,其灰度图中某一行相邻的8个像素如上图所示。
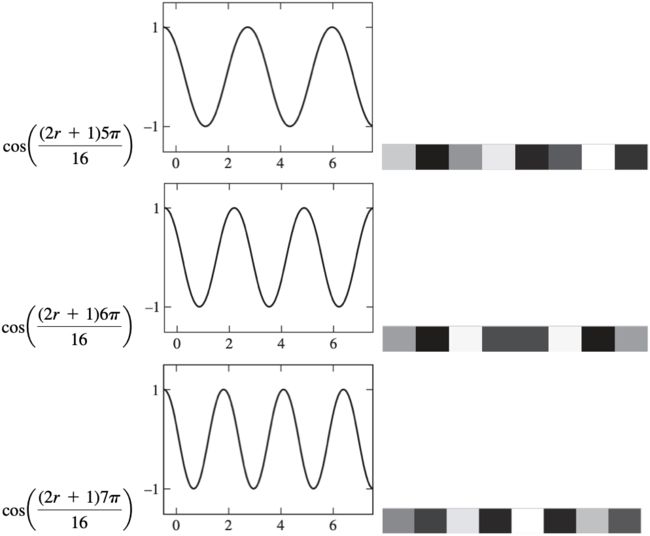
我们选定了8个基础波形。并根据每一个波形图计算出8个像素。如上图所示,最左侧的函数为基础波形的三角公式,中间的图形为其波形图,右侧的像素行是根据这个基础波形计算出的前8个有效的像素值。
前面已经提到,任意一行像素都可以使用二维的波形表示。而这些二维波形一定满足狄利克雷条件,他们一定能够被分解为多个基础波形的组合。我们现在要做的就是需要计算出各个基础波形的系数,换句话说也就是函数在频域的取值。这个可以由离散余弦变换公式计算,一维的离散余弦变换公式如下。
在上面的公式中f(r)为空域函数,对于灰度数字图像处理而言,也就是某行像素的具体灰度值,r是像素点的坐标,M是该行像素的总数量。u可以理解为频域函数的频率取值,cos后的括号的内的部分就是基础波形的三角函数。需要注意的是,频域函数的频率取值个数和空域函数的自变量取值个数是相同的。对于数字图像而言,也就是一行有几个像素,就能得到几个频率分量。
使用上面的公式,我们可以计算出频域函数的值,由于例子中该行像素有8个像素点,我们能够计算出8个有效的频域分量,即F(u)在[0,7]的值和离散余弦变换公式中常数的乘积分别为[w0 ~ w7] = [389.97, -280.13, -93.54, 83.98, 54.09, -20.51, -19.80, -16.34],他们就是在将基础波形混合为原始波形时各个基础波形的系数。也就是说所有频率分量的食欲函数和其系数相乘后的和就是原始的图像。
上图是使用基础波形得到的图像合并原始图像的示意图。需要注意在离散余弦变换得到的频率分量重,F(0)称为DC分量,F(1)到F(M-1)称为AC分量。这个词来源于模拟电路,DC分量和直流电路相关,AC分量与交流电路相关。
数字图像具有二维的物理特性,因此实际上我们在处理数字图像时使用到的是二维的离散余弦变换。其公式如下。
对于灰度数字图像,在上面的公式中空域二维函数为f(r, s)描述了原始的图像在像素坐标(横坐标为r,纵坐标s)上的灰度值,M和N分别为横向和纵向的像素数量,(u, v)是空间频率,两个cos函数的乘积为为基础二维空间波的函数,F(u, v)是描述原始图像的空域函数f(r, s)是频域上的对应函数,其u和v的有效取值分别为[0, M-1]和[0, N-1],函数F(u, v)的每个值都是对应的二维空间波形的系数。
需要注意的是离散余弦变换在图像处理领域通常被限定在一个8乘8的像素子块,也称为宏块中。这样能够极大的减少计算复杂度,提升图像处理效率。这是JPEG图片压缩和MPEG视频压缩中最重要的一步,当然不同的编码标准对于宏块的尺寸选择有所不同,但是通常是在8乘8,以及16乘16两种尺寸之间选择,在后续文章数字视频还会详细的讲到。
上图是一个8乘8的像素宏块,我们统计其中的灰度值得到如下的颜色矩阵表。
我们再利用刚介绍的二维离散余弦变换计算出其各个空间频率分量的的系数,也就是函数F(u, v)的值,得到如下的频率分量振幅矩阵。和一维离散余弦变换公式类似,F(0, 0)称为DC分量,其余值称为DC分量。
如同一行像素可以通过一维离散余弦变换分解为多个基础函数,再由这些函数复合还原。一张二维的数字图像也能通过二维离散余弦变换分解为多个基础函数,再由这些基础函数合成。不同的是一维离散余弦变换分解得到的基函数可以用二维波形表示,而二维离散余弦变换分解得到的基函数都要用空间三维波形表示。二维离散余弦逆变换的公式如下。
对于前面例子中8乘8的像素宏块,在二维离散余弦逆变换的公式中需要由8乘8,一共64个基函数组成,每一个基函数都可以被表示成二维波形,而每一个波又可以表示为简单的二维图像,如下图。
每个图像都是二维离散余弦逆变换公式最后两个余弦分量在离散点P(r, s)上的取值相乘的结果,其中r和s的取值空间都是[0, 7]。
任意8乘8二维图像都可以由上面的基函数合成,每个基函数的系数也就是权重可以由二维离散余弦变换计算。除去常数的部分F(u, v)的值又称为频率分量振幅矩阵。对于使用RGB颜色模型的彩图而言,只需要分别对3个通道单独处理即可,也就是3次DCT处理。
上面的8乘8像素宏块例子的频率分量振幅矩阵和二维离散余弦逆变换公式中常数的乘积,与其对应的基频函数相乘,最后再求和就可以合成原始的二维图像。
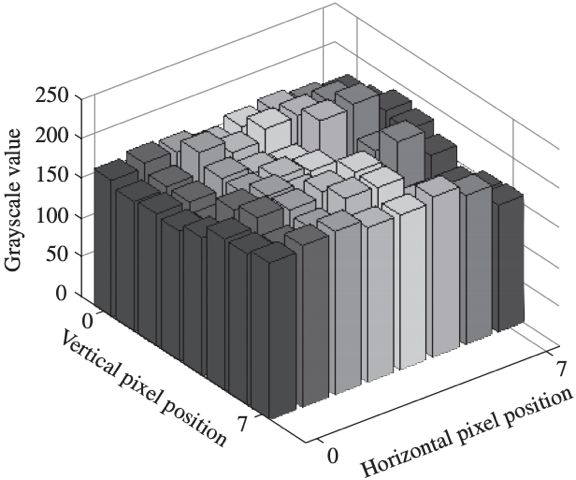
下面让我们来看看更实际的例子,还是之前的小鸟图,我们选取了其中一个8乘8的像素宏块如下图。
我们使用z轴表示每个像素点的颜色值,xy轴分别表示水平和垂直方向上像素的索引值,绘制出如下的空域像素直方图。
我们利用二维离散余弦变换计算出其每个频率分量的系数,也就是频域函数F(u, v)的取值,我们使用z轴表示其F(u, v)的取值,使用xy轴分别表示在水平和垂直方向上的频率。最后我们得到如下的频率分量振幅直方图。
我们可以看见上面的频率分量振幅直方图中,DC分量最大,还有一些较小的AC分量,将它们和二维离散余弦变换公式中的常数项乘积作为基频函数的系数,既可以还原出原始图像。
这里需要注意的是,在频率分量振幅直方图中除了离坐标原点的几个频率分量有值外,其余AC分量取值几乎为0。也就是说我们完全可以舍弃右下角的频率分量,仍能还原出原始的图像,这是因为右下角的空间频率极高,从心里学的角度讲已经超出了人眼的分辨精度的缘故。这样的处理方式也是JPEG压缩、MPEG中帧内压缩的理论基础。
4 失真
4.1 模糊效应和块效应
尼奎斯特频率在数字图像上的应用可以理解为,当横向和纵向的采样率低于人眼敏感的最高频率两倍时得到的图像就会发生失真。当得到的样本放大到原始大小后会出现明显的锯齿和块效应。
我们使用合适的采样率排出的照片如下。
而当我们使用过低的采样率就会拍摄出如下的图片。这种现象也被称为过疏采样。
4.2 摩尔纹
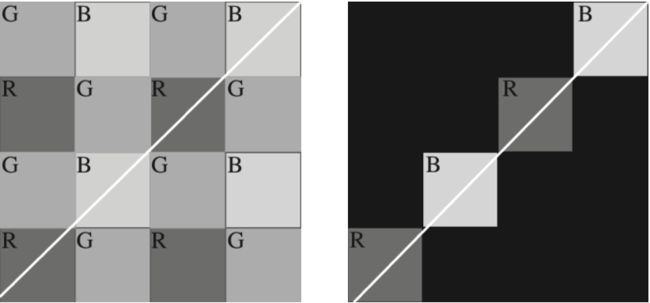
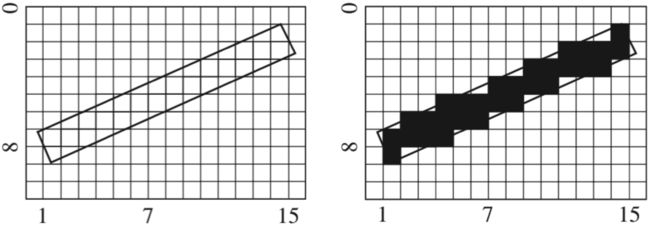
莫尔纹(Moire Patterns)指在数字图像采样过程中,当采样频率不足够但是很接近能够捕捉到原始的图片细节时,得到的高频干扰的条纹,是一种会使图片出现彩色的高频率不规则的条纹。另外当采样方向和原始图像的纹理方向有一定夹角时也会得到摩尔纹。
如在上图中,左侧的图像的纹理和采样的方向呈一定程度的夹角,同时采样的频率和原始图像的频率接近,我们假定一个样本内黑色的部分超过其面积的一半则采样得到的结果为黑色,反之则为白色。这样我们最后的到的图像为右图,我们可以看到图像已经明显失真,这就是有趣的摩尔纹。
当我们了解什么是摩尔纹后,回忆一下当我们看见透明的窗帘折叠后发出的闪光效果,透过屏幕看编织的椅子的出现的漩涡效果,这些都是生活中常见的摩尔纹。
同样的我们考虑生活中的实际图像,一个由具有高频纹理材质的背包如下图。
对于这种类型的场景,当我们的采样率和原始图片频率不同步时就很有可能出现摩尔纹,如下。
而实际的原始图像如下。
在使用数码相机拍摄图片时出现摩尔纹可以通过倾斜相机的角度、改变焦距或者更换镜头解决。这会改变采样的方向和广义的原始图像空间频率。
4.3 相机中图片的感知方式
传统相机使用覆盖银涂层的胶卷成像。胶卷分三层,分别对红、绿和蓝三色光敏感。
数码相机使用电耦合器件(Charge-Coupled Device,CCD)技术来感知光和颜色,互补金属氧化物半导体(Complementary Metal-Oxide Semiconductor,CMOS)是另外一种新的感光技术。
其中CCD由一个二维的像点阵列组成,每个像点对应了一个样本(数字图像上的一个像素),每个像点都被红色、绿色和蓝色的过滤器所覆盖。
而CCD的实现方式有4种。第一种将入射光分为3束,在每个感光点有3个传感器,每个传感器分别只能感知红、绿和蓝色。这样做的好处是每个像素点都能直接得到原始的3色值,但是缺点是昂贵,并且导致相机体积过大。
第二种会在拍照时旋转传感器,这样能够连续的感知红、绿、蓝三色光。这种方式的缺点是3种颜色不能同时被感知,只能拍摄静止图片。
第三种方式如Foveon X3使用硅传感器,使用了垂直叠加技术。不同深度的硅吸收不同波长的光,因此能够在一个像点上同时感知三种颜色。
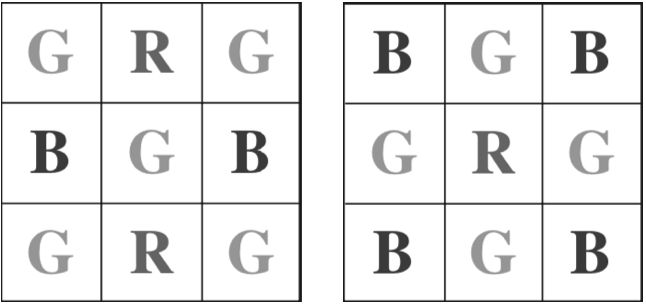
第四种方式也是最常见的方式是使用拜耳颜色滤镜,每个像点只感知一种颜色,使用插值计算的方式计算另外两个分量的值。这种方式虽然廉价,但是有时会导致颜色会失真。
上图是一个拜耳颜色滤镜示意图,在拜耳颜色滤镜总绿色感光像点的数量是另外两种像点的两倍,这是因为人眼对绿光更敏感。
在得到原始数据后,我们需要通过插值计算像素点的颜色,这种颜色计算的方法称为去马赛克算法。其中一种最简单的方法是最近邻近法。对于每个采集到G分量的像点计算R和B分量的值时只需取相邻2个像点的平均值即可。计算采集到R和B分量的像点其另外两个分量的值时需要取相邻4个像点的平均值。其计算区的临近颜色点如下图所示。
插值算法本质不能很好的重建要拍摄的场景,因此在这个过程中存在一定失真,如莫尔纹、块和斑点。
如上面左图,假设拍摄一根白色的线,这条线正好穿过了CCD传感器,假设线的两边都是黑色。那么其他像点感受到的光强都为0。如右图,在进行插值计算时,对于白线穿过的像点而言,其每个像点计算插值时从相邻像点取到的值总为0,因此对于白线穿过的像点它们的颜色无法从其相邻的像点计算得到,最后我们就会得到失真的图像。
有些相机在镜头上使用去网纹或抗锯齿镜面,这能够有效的将图片模糊一些从而减少颜色失真。相机制造商将其作为可选特性,可以在设置中开启抗锯齿滤镜。但通常高质量的相机不提供这个功能。
4.4 锯齿状边缘
在计算机屏幕上渲染一条斜线时有时能看见锯齿状的边缘,这种失真是由于计算机有限的分辨率所导致的。几何学中,线是由无限的点所组成,而计算机屏幕上的线是由离散的像素组成。
在上图中,左侧图像是实际的2像素直线,假设当每个样本内部被覆盖的区域超过一半时,我们便将该样本涂成黑色,那么我们就会得到右图所示的带锯齿的直线。
抗锯齿是一个减少直线锯齿程度或者边缘失真的技术。一种可行的方式沿着线的边缘给像素涂上指定的颜色,颜色与被覆盖的比率成正比,并和线上最接近的点颜色相关。
如上图,位图在放大时通过上采样增加像素值,其像素的颜色通过插值计算获得,这样会突出锯齿状的边缘。
如上图,矢量图因为是实时绘制,因此当放大时,其失真程度相对位图而言并没有那么严重。
5 颜色
颜色学是一门独立有趣的学科,这里只会介绍最重要的基本知识,更多的细节可以参考如下两本参考书。
5.1 颜色感知和表示
颜色既是物理现象(电磁波),也是心理现象(当这些电磁波落入到人眼的颜色感受器中,以一种不太明了的方式,人脑控制电磁波与眼睛之间的交互,这就是颜色感知)。自然界中我们所感受到的颜色都是不同波长的组合。
现代解剖学研究表明人眼上存在3种类型的视锥细胞,分别为L、M和S类型的视锥细胞,它们分别对长波、中波和短波的电池波敏感,如下图。
而自然界中的物质对不同波长的电磁波反射率是不同的,如菠菜的叶子主要反射波长为550nm左右的电磁波。反射出的电磁波再被视锥细胞感受到最后在大脑中便产生了颜色的主管概念。
牛顿最早对颜色进行了系统的研究,他发现颜色可以通过混色所得,并在其林文中提出了色轮的概念,也被称为牛顿色轮,如下图。
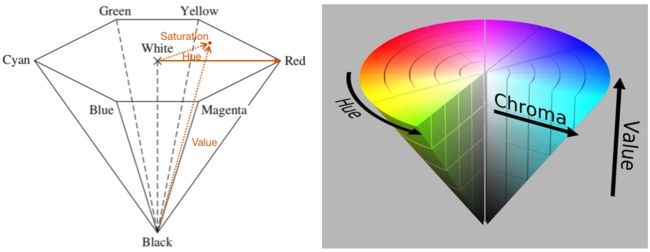
颜色的三要素是色调(色相),饱和度(纯度)和明度。其中色调(Hue,也称色相)可以理解为颜色的主波长,在圆形的外围是通过分解白光得到的所有单位能量的单色。色调的起点为红色,向黄色方向递增。
饱和度(Chroma,也称纯度)可以理解为是往单色中参杂白光的量,如果白光参杂足够多,则饱和度越低,也越接近灰色。
明度(Brightness)是主观概念,和观察者的感知相关,表示人眼感受到的色彩发光强弱,通常将单位能量的单色明度值定义为1,逐渐减小其光强,明度也跟着降低,当光强度变为0时,其明度值也为0。
需要注意的是亮度(Luminance)、明度(Brightness)和光亮度(Lightness)这三个词很容易被混淆,其实它们都有不同的含义。
其中亮度指的是人眼对光的辐射出的能量感受值,器单位是尼特,即坎德拉每平方米。通常我们说到亮度时都是指的相对亮度,即其Y/Yr,Yr指参考白光的亮度。
明度指的是我们的视觉感受到的发光量是多还是少,这是一个很主观的概概念,它并没有世界的数学定义。而亮度则不同,它有着明确的数学定义,它和光的波长、能量,以及人眼感受到的明亮感相关。有趣的是不同波长相同功率的光,人眼会觉得550nm的波看上去最亮。
光亮度指的是颜色和同样光照环境下白色的相对明度。
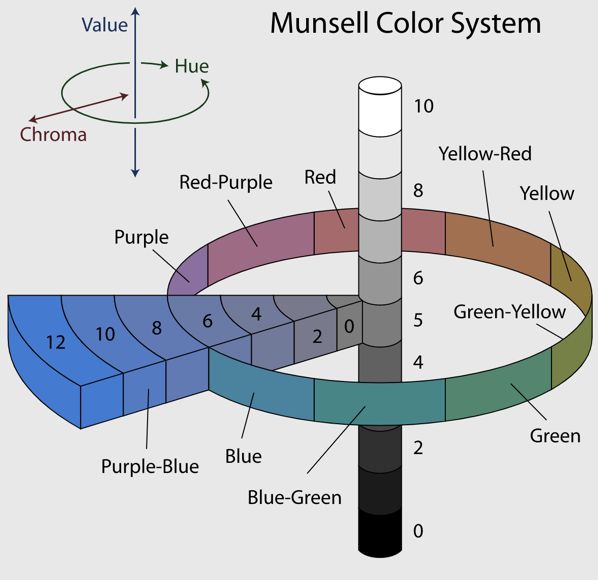
下图中的孟赛尔颜色系统是较早的一个系统描述颜色的方法,它通过光亮度(Value)、色调(Hue)和饱和度(Chroma)三个维度来描述一个颜色。
表示颜色的一种科学方法是光谱密度函数,但是通常不用在计算机系统中。因为多个光谱密度函数可以表示人眼所感知到的同一种颜色。
上图描述了一个简化的光谱密度函数,其中色调由主波长决定,亮度由函数围成图像面积决定,饱和度由尖峰部分占总面积的比率决定,其计算公式如下。
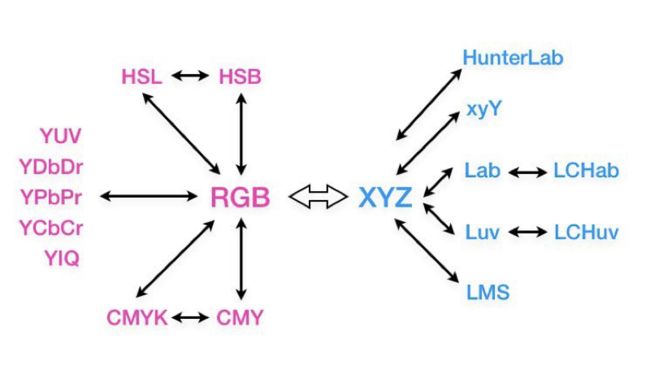
常用的颜色的颜色表示方法有很多种,他们呗称为颜色空间。主要包含RGB,CMKY,圆锥转换(Cylindrical transformations),标准CIE,亮度+色度5种颜色模型系列。
5.2 RGB颜色模型族-RGB颜色模型
RGB是基于波长的常量,rgb为每个常量分量的系数,也叫颜色通道。需要注意的是RGB颜色模型未定义使用的三种光的波长。
如上图,RGB颜色模型中所有颜色都是三原色混合的结果,红、绿、蓝三色的补色分别为青、品红和黄色。数学模型中rgb的取值范围为0~1,在图像处理程序中通常为0~255。心理学的研究表明,人眼对绿色最敏感,利用对三种颜色的敏感程度得到从RGB颜色模型计算灰度即亮度的公式如下。
5.3 CMYK颜色模型族-CMYK颜色模型
CMY是减色模型,分别表示在白光中扣除红、绿、蓝三色分量的比例。该颜色模型和RGB颜色模型的转换公式如下。
由于CMY混合的结果并不是纯黑色,因此在CMYK颜色模型中引入K分量表示纯黑色。其转换公式如下。
5.4 圆锥转换颜色模型族
根据颜色本身的色调(基本颜色)、饱和度、明度或者光亮度表示颜色。色调-饱和度-纯度(Hue-Saturation-Value,HSV)颜色模型也称色调-饱和度-明度(Hue-Saturation-Brightness,HSB)颜色模型如下图所示。
色调-光亮度-饱和度(Hue-Lightness-Saturation,HLS)颜色模型。
5.5 CIE颜色模型族和色域
国际发光和照明委员会(CIE)做了一项颜色混合实验,实验使用了波长分别为700nm,546.1nm,435.8nm的标准红绿蓝光作为三个单色光,参与则被要求控制这三种单位能量光的含量直到他们认为这与可见光谱中单位能量的单色光是同一个颜色。并据此绘制出了颜色匹配函数如下图。
实验表明如果想要使用RGB三色光混合出自然界中的所有单一波长的纯色光,有时还需要在绿色和蓝色混合光中扣除部分红光,即给纯色加上红色的光。
另外没有任何计算机的显示器能够通过自身红、绿、蓝三色光的方法组合出所有的可见光。一台给定显示器能够显示的颜色范围称为色域。相同颜色模型的不同型号显示器可能有不同的色域,同样在同一台显示器上使用不同的颜色模型一定有着不同的色域。
5.5.1 CIE-XYZ颜色模型
根据此实验结果,国际发光照明委员会于1931年提出CIE XYZ颜色模型,用上图的公式表示,假设理论上存在3种单一波长的可见光X、Y、Z,使得三个分量的能量函数取值都为正。并且通过刻意的选择,使得上式中Y的系数和发光效率函数的数学模型具有相同的形状,也就是说Y可以理解为亮度。
RGB颜色模型和CIE-XYZ颜色模型可以通过如下的公式进行转换。
为了更方便表示各种颜色模型的重叠区域,需要在二维平面下绘制色域图。首先对XYZ三个分量的能量函数进行标准化,其计算公式如下。
则CIE-XYZ颜色模型参数函数表示如下。
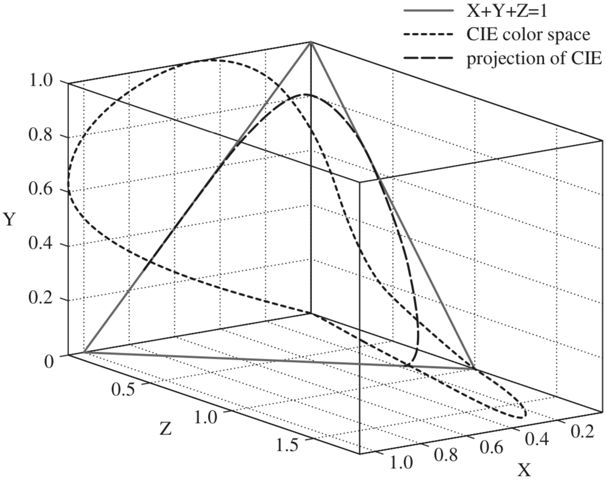
在三维空间中,绘制出色度分量和为1的平面。该平面为CIE-XYZ颜色模型中所有颜色的色度投影平面,即它能表示所有颜色的色度信息。
将CIE-XYZ颜色模型所有单位能量的饱和颜色,即所有可见光光谱中的单位亮度单色颜色的CIE-XYZ颜色模型表示投影到色度平面中如下图。图实线表示的是色度投影平面,即X+Y+Z=1的平面,短须表示的是所有单位能量的饱和颜色,粗虚线表示的是这些饱和颜色在色度平面上的投影。
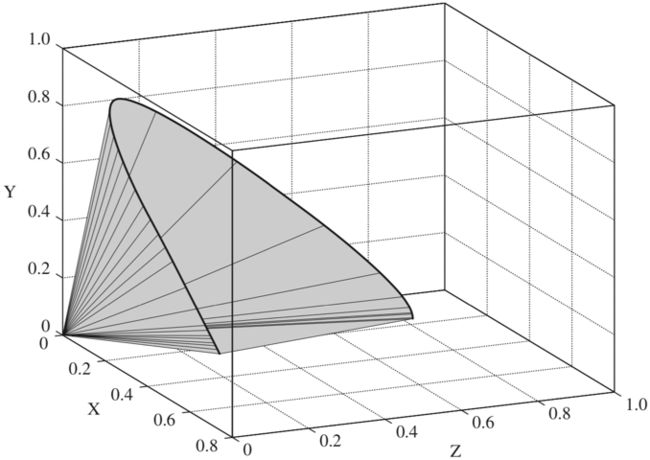
如下图马蹄形轮廓和原点的连线形成一个圆锥,表示CIE-XYZ颜色模型中的不同能量的所有可见光谱单一颜色。无限延伸该平面,该平面上及其内部的点能够表示所有甚至超越可见的颜色。
5.5.2 色域
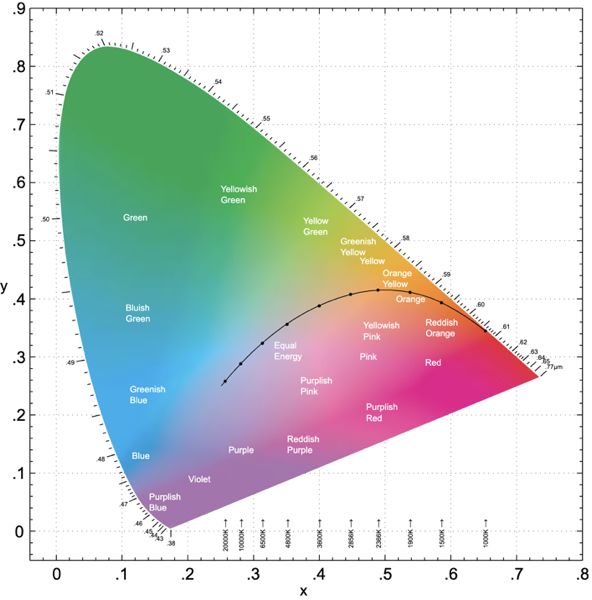
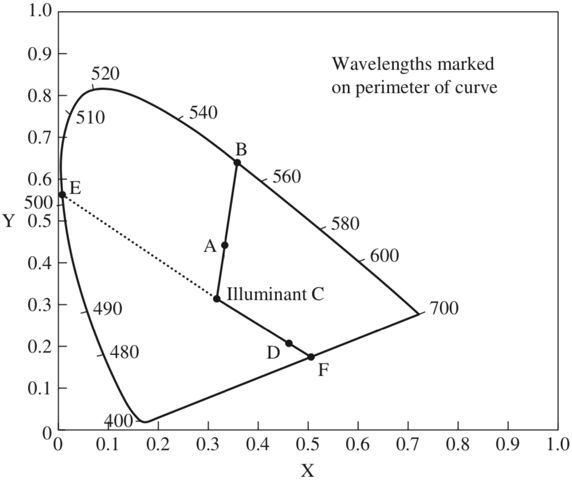
如下图,色度平面上的马蹄形轮廓在z=0的平面上投影称为CIE色度图。CIE色度图能够直观的观察不同颜色模型的色域范围。但是颜色是3维现象,CIE色度图在二维空间中表示颜色,忽略了能量。所以不能表示所有颜色,如棕色,是一种低亮度的橘红色。
转换后的RGB和CMKY颜色模型的色域在CIE-1931色度图中表示如下图。从图中我们可以看出没有一个计算机能够识别的颜色空间能够表示出所有的颜色。它们都存在色域限制。
下图演示了如何计在CIE色度图中计算一个颜色的色调和饱和度,其中中C点称为白光C,也称满饱和白。马蹄形边缘上表示的是满饱和度的光谱颜色。底部直线上的颜色是不能通过单波长光谱产生的颜色。
主波长决定了一个颜色的色度,可以由该颜色点到C点的连线到马蹄形边缘的交点确定,如颜色A的主波长约为550nm,为暗绿色。如果交点在底部直线上,如颜色D的交点为F,则颜色D称为非光谱色,颜色E为其补色的主波长。饱和度可以通过表示颜色的任意一点和C点的连线确定,如AC/BC。
5.5.3 色温
对于颜色而言我们还会遇到另外一个概念,那就是色温。需要注意的是这里要和冷色调暖色调相区分,冷暖色调指的是心理感受,通常蓝色系被称为冷色调,红色系被称为暖色调。而色温指的是加热绝对黑体时,颜色由红到白,最后变为蓝色时,绝对黑体的温度也就是其对应颜色的色温。CIE-LUV色度图中的色温曲线如下图所示。
这里还需要注意的点是,我们说CIE-XYZ颜色空间是一个设备无关的颜色空间,并且前面讲到颜色匹配函数时也说到过是通过和可见光谱的单位能量存色做的对比,CIE-XYZ颜色模型建议我们使用D65,也就是7000k的白色来作为单位能量。
5.5.4 感知均匀性以及CIE-Lab,CIE-LUV颜色模型
感知均匀性指的颜色模型在数值上的变化和人眼所感受到的颜色成线性变化关系。RGB和CMKY颜色空间都不是感知均匀颜色空间,而CIELAB和CIELUV是感知均匀性的颜色空间。
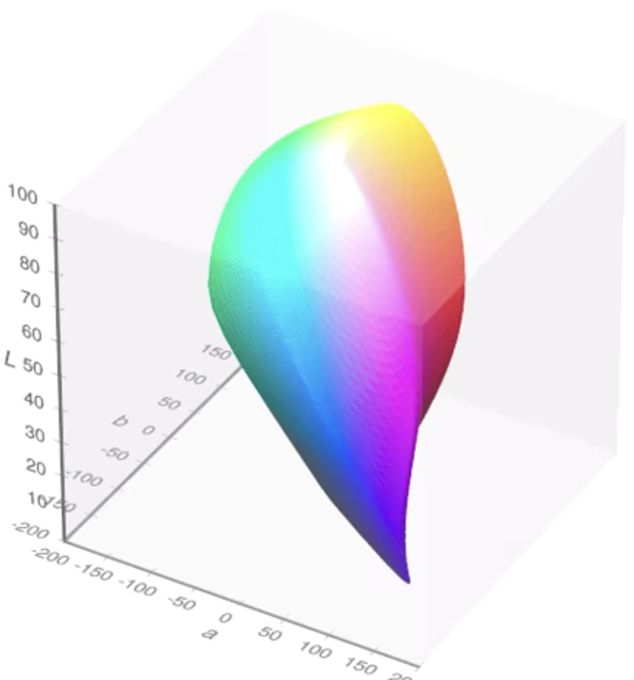
CIELAB颜色模型如下图,其中中L轴表示光亮度值从0~100变化,对应了黑色到白色。A轴表示色度从绿色(负)到红色(正)变化,B轴表示色度从蓝色(负)到黄色(正)变化。另外CIELAB是一个减色模型,被用于各种颜色转换的中间模型。
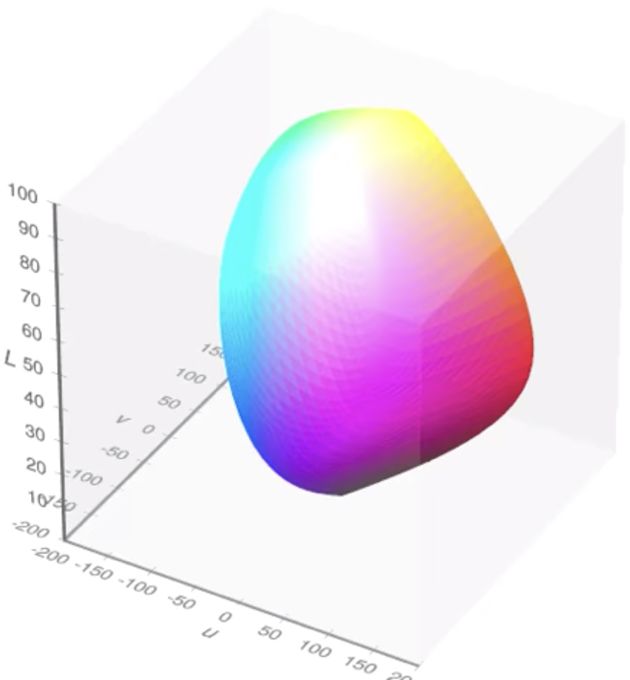
CIELUV颜色模型如下图,其中L轴表示光亮度值从0~100变化,对应了黑色到白色。U和V轴为色度轴,没有具体的含义。另外CIELUV颜色模型是一个加色模型。
通过CIE-LUV得到了新的CIE-LUV色度图如下图所示。
5.6 亮度和色度颜色模型族
亮度颜色模型通常用于数字视频领域,指的是通过提取颜色的1个亮度分量,和2个颜色分量来描述颜色的颜色模型,他和CIE颜色模型族的区别是亮度和色度颜色模型族都是设备相关的,而CIE颜色模型族是设备无关的。
常见的亮度和色度颜色模型是YIQ颜色模型,它可以有RGB颜色模型转换而得,其转换公式如下。
亮度和色度颜色模型的发展有两个原因。第一,早期的电视播出的是黑白信号,而后来彩色电视发展起来的时候需要兼容早期的黑白电视,而使用亮度和色度颜色模型就可以使用黑白电视只使用亮度信号,而彩色电视使用三个分量信号,这样就能在传送同样的信号前提下既支持黑白,也支持彩色电视的播放。
第二,因为人眼对与亮度的敏感层度会明显高于对色度的敏感程度,使用亮度和色度颜色模型后,通过适当的丢弃一些色度信号就能很大的提升视频的压缩效率。
实际上常见的用于电视信号的颜色模型一共有三种,它们在世界范围内的分布情况如下图下图。其中YIQ用于美国国家电视委员会主导的电视格式(National Television System Committee,NTSC)。YUV颜色模型用于欧洲的逐行倒相制(Phase Alternation Line,PAL)的模拟视频标准的。YDbDr用于法国主导的顺序存储电视格式(Sequential Color and Memory)。
另外,常见的亮度和色度颜色模型还有YCbCr,它常用于JPEG和MPEG格式压缩处理中。这些不同的亮度和色度颜色模型区别在于通过RGB颜色模型转换时其矩阵的值选取不同。这是因为不同标准的电视其硬件发出的3个单色光的频率和能量都有所区别的原因。
5.7 颜色管理系统
某种颜色空间的颜色,在不同的光线环境中,不同的设备上,以及颜色空间转换时可能会出现颜色失真。而颜色管理系统可以在颜色空间、基色设置和从颜色值到像素和油墨到物理表现的绘制过程中,完成从一个硬件设备与另外一个硬件设备的交换。CIE颜色空间是一个通用的,独立于硬件的颜色空间,通常CIE-LAB作为中间转换颜色模型。常见的颜色空间转换方式如下图。
颜色管理分为校准显示器、描述显示器的颜色配置、创建图像独有的颜色配置、保存颜色配置和图像、在其他设备或者程序中重置图像的颜色。
6 矢量图
6.1 几何图形
矢量图是一种由分割明显,颜色单一的区域组成的图像。通常用于卡通、商标等图像。
图像格式尽管很多,但是它们背后描述图像的数学公式非常相似,如两个端点确定一个线段,一个边长确定一个正方形等。对于曲线而言,可以选取一系列控制点,然后利用数学公式平滑的绘制出一条曲线,如厄米曲线(Hermite)、贝塞尔(Bezier)曲线、自然样条曲线(Natural cubic splines)。
6.2 曲线的函数表现方式
参数化三次多项式函数能很好的描述曲线。一个N次多相似函数表示如下。当n为3时,如下函数能够很好的描述一条曲线。
函数的三种表现方式为显函数、隐函数,和参数函数。其中显函数表示如下。
隐函数表示如下。
参数函数表示如下。
表示曲线的带三次多项式的参数函数如下。
其矩阵形式表示如下。其中ax…dy矩阵为参数矩阵,需要根据控制的的坐标以及曲线类型计算。
其简写形式如下。
对于给定的控制点,将它们连接成曲线的方式有多种,在不同的环境下可以根据它们的优缺点选择最适合的方式。总的来说分为内插值算法和进似算法。
内插值算法需要将所有控制点直接连接成一条曲线。如Hermite曲线和自然三次样条曲线。进似算法计算出的曲线不需要通过所有的控制点,如贝塞尔曲线。近似算法允许移动单一的控制点,在不影响其他部分的前提下,仅更改曲线的一部分,称为局部控制。
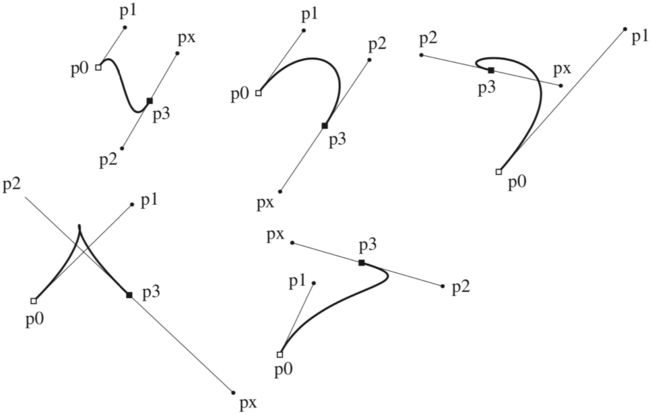
6.3 贝塞尔曲线
贝塞尔曲线由许多控制点近似形成的曲线。这里讨论最简单的由4个控制点组成的贝塞尔曲线。定义:4个控制点分为两个终点P0和P3,两个内部控制点P1和P2。控制点P0和P1的连线、以及P2和P3的连线分别是曲线的两条切线。可以得如下两个方程。
根据P0和P3是曲线的起点和终点可以得到如下两个方程。
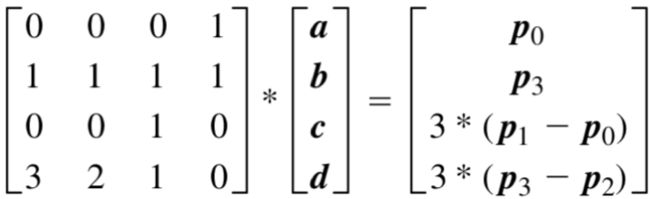
将上述的4个方程写为矩阵形式可以得到。
通过矩阵的转换,最后算出参数矩阵C和控制点矩阵G的关系如下。
最后得到曲线上任意点Pt的函数如下。M称为基矩阵,G称为集合矩阵。
在贝塞尔曲线的矩阵基础上再次转化可以得到如下曲线复合函数。其中四个参数称为伯恩斯坦(Bernstein)多项式。
对于复杂的贝塞尔曲线,对n次多项式都适用的通用公式如下。
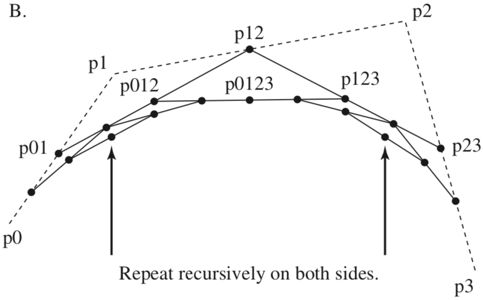
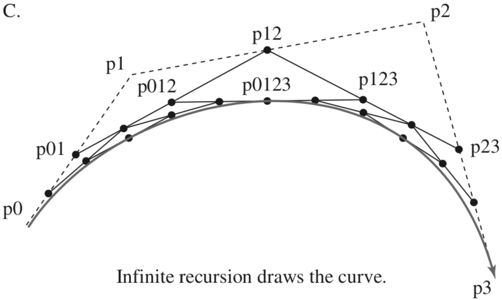
描述三次贝塞尔曲线的方式是适用算法描述。下图中De Castejau算法描述了如何通过4个的控制点递归建立一条贝塞尔曲线的过程。
程序中绘制贝塞尔曲线的方式如下。
6.4 算法艺术和程序建模
算法艺术(也称程序建模)是除位图和矢量图之外的第三中图像格式。它通过基于数学计算或者独特的算法来编写计算机程序,创建数字图像。它和矢量图的区别在于,后者基于已经想象好的具体几何形状,而后者却不是。
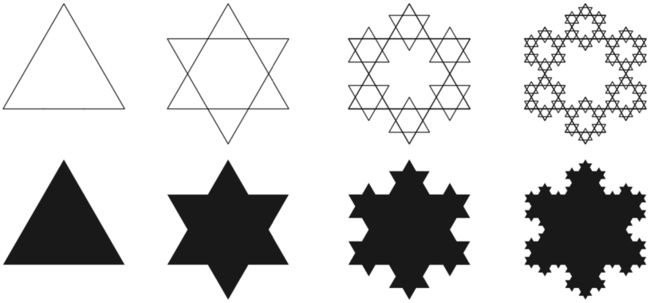
算法艺术最好的例子就是分形图像的生成。分形是一种具有递归循环结构的图像。自然界中的分形结构如下。
下图中的科赫雪花(Koch snowflake)是算法艺术的例子。
下图中的谢尔宾斯基垫片(Sierpinski’s gasket)同样也是算法艺术的例子。
Mandelbrot分形并没有明确创造出一个无穷重复形状的分形,而是通过计算本身得到一个美丽复杂的几何形状。
Julia分形是Mandelbrot分形的一种变种,如下图。