4. 数据结构－ AVL 树

这篇文章收录在我的 Github 上 algorithms-tutorial，另外记录了些算法题解，感兴趣的可以看看，转载请注明出处。

(一) AVL 树概念

AVL 树(也可以称为平衡树)是一类数据结构，是改进后的二叉查找树。一般的二叉树的查询复杂度是跟目标结点到树根的距离 (即树深) 有关，因此如果当结点的深度普遍比较大时，查询的成本就会上升，所以 AVL 树就应运而生。

AVL 树可以理解为平衡树树的一种具体实现，两者并无二致。这里介绍的平衡树跟老师说的AVL 树不一样。

一、AVL 树特性：

AVL 树本身首先得是一棵二叉搜索树
每个结点的左右子树的高度之差的绝对值 (平衡因子) 不超过 1
每个结点的左右子树也要满足特性 2，也是平衡二叉树

平衡因子：某结点的左子树与右子树的高度(深度)差即为该结点的平衡因子

AVL 树上所有结点的平衡因子只可能是 -1，0 或 1。

比如：

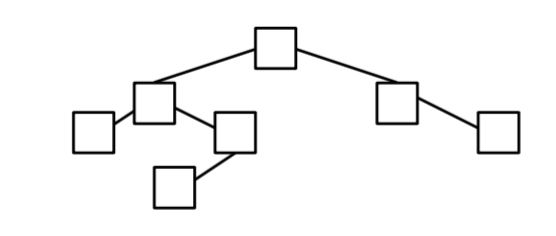
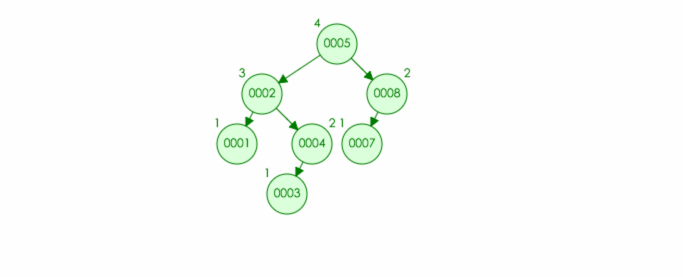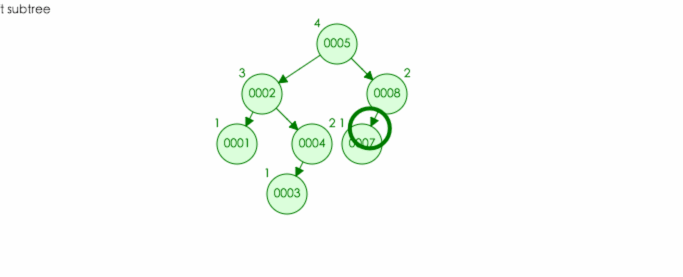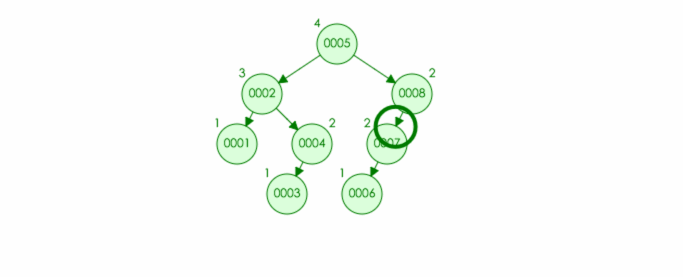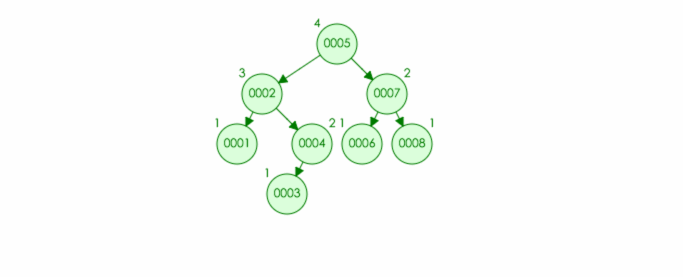
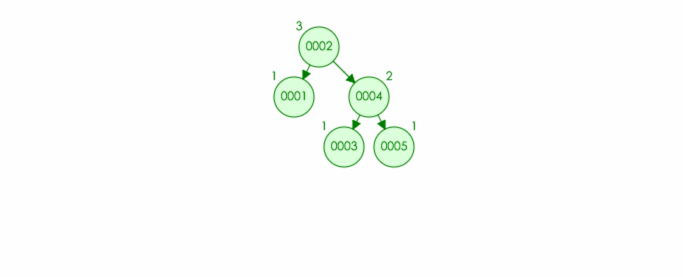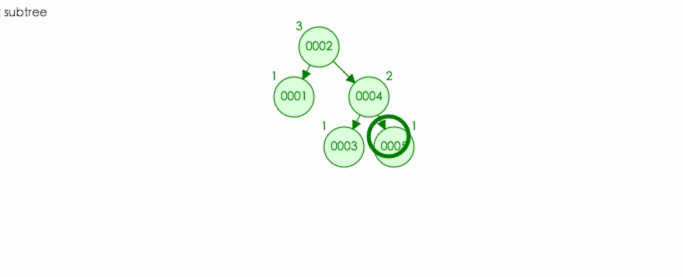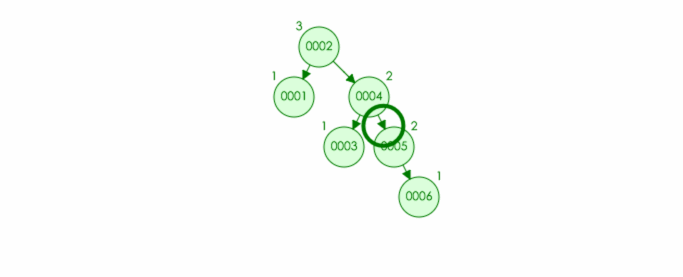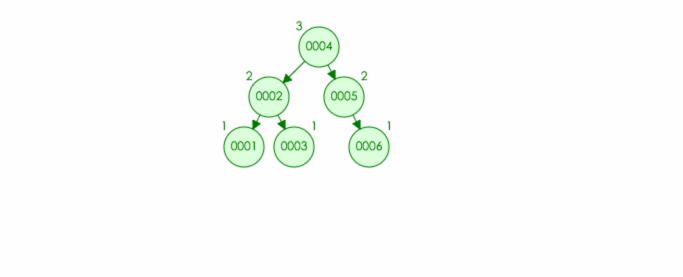
AVL 树：

1.png

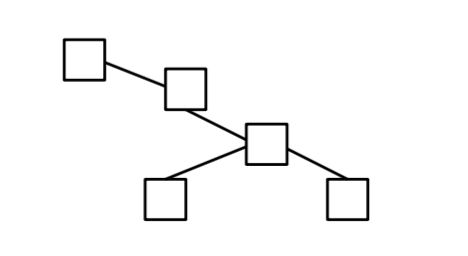
non-AVL 树：根节点无左子树

2.png

二、为什么使用 AVL 树？

3.png

我们都知道二叉搜索树可以具有良好的查询，插入等操作，但是如果二叉树退化成了链式树(上图右)，那么其空间复杂度也会从原本 O(logn) 退化成了 O(n)，这样显然是不想看到的结果。

如果可以让树维持矮矮胖胖的好身材, 也就是让高度维持在 O(log n)左右, 完成上述工作就很省时间。能够一直维持好身材, 不因新增删除而长歪的搜寻树, 叫做 AVL 树。

(二) AVL 树基本操作

相对于二叉查找树的节点来说，我们需要用一个属性二叉树的高度，目的是维护插入和删除过程中的旋转算法。

JAVA 代码实现:

public class AVLTree{
    TreeNode leftChild = null;
    TreeNode rightChild = null;
    int height;
    String data;
}

那么我们在对一棵二叉查找树进行插入和删除操作的时候，如何让其保持 AVL 树的特性呢？

一、旋转：

假设有一个结点的平衡因子为 2(在 AVL 树中，因为结点是一个个插入到树中，一旦出现不平衡的状态就会立即调整，因此平衡因子最大不可能超过 2)

那么这时候就要进行调整了，由于任意结点最多只有两个儿子，所以当高度不平衡时候，无非以下情况所造成：

对该结点的左儿子的左子树进行了一次插入。
对该结点的左儿子的右子树进行了一次插入。
对该结点的右儿子的左子树进行了一次插入。
对该结点的右儿子的右子树进行了一次插入。

情况 1 和 4 是关于该点的镜像对称，同样，情况 2 和 3 也是一对镜像对称。

当那个结点高度出现不平衡，我们就要对那个结点进行操作，这里我们称这个不平衡结点为当前节点。

二、单旋转：

情况 1 和情况 4类似，我们可以理解为发生在 “外边” 的情况 (即左-左，右-右的情况) 该情况只需要通过一次旋转来完成调整

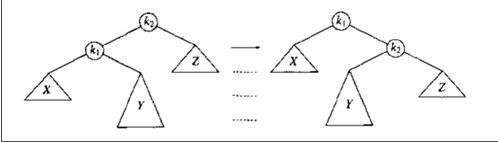
情况 1：对该结点的左儿子的左子树进行了一次插入

4.png

此时结点 k2 出现了不平衡，所以我们以 k2 为当前节点进行右旋，并将 Y 移到 k2 左子结点，从而变成右图（因为左边高度高，所以我们将左子树上移，来平衡其高度差，很好理解）

代码实现：

public AVLTree singleRotateWithRight(AVLTree unbalancedNode){
    AVLTree node = unbalancedNode.leftChild;
    unbalancedNode.leftChild = node.rightChild;
    node.rightChild = unbalancedNode;
    node.height = MAX(node.leftChild.height, node.rightChild.height) + 1;
    unbalancedNode.height = MAX(unbalancedNode.leftChild.height, unbalancedNode.rightChild.height) + 1;
    return node;   //返回新的根结点
}

实例：插入结点 6

1.gif

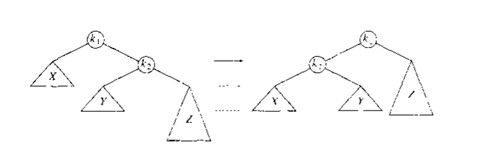
情况 4：对该结点的右儿子的右子树进行了一次插入

6.png

思路和情况 1 类似，操作刚好相反过来

代码实现：

public AVLTree singleRotateWithLeft(AVLTree unbalancedNode){
    AVLTree node = unbalancedNode.rightChild;
    unbalancedNode.rightChild = node.leftChild;
    node.leftChild = unbalancedNode;
    node.height = MAX(node.leftChild.height, node.rightChild.height) + 1;
    unbalancedNode.height = MAX(unbalancedNode.leftChild.height, unbalancedNode.rightChild.height) + 1;
    return node;   //返回新的根结点
}

实例：插入结点 6

2.gif

三、双旋转：

情况 2 和情况 3 (由于其形状可以称为 dog-leg)是插入发生在“内部”的情况（即左-右的情况或右-左的情况），该情况要通过稍微复杂些的双旋转来处理。

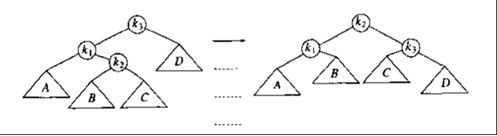
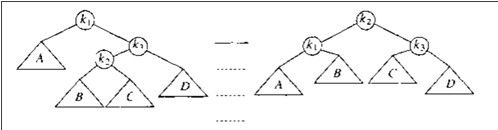
情况2：对该结点的左儿子的右子树进行了一次插入。

这种情况是单旋转调整不回来的，如下图，旋转后还是不平衡

8.png

这时候需要旋转两次来达到平衡效果：

9.png

以 k1 为当前结点进行左旋，再以 k3 为当前结点进行右旋

代码实现:

public AVLTree doubleRotateWithRight(PAVLNode unbalancedNode){    //之所以称为 Right，是因为最后不平衡结点变为右子树，这样比较好记
    /* Rotate between K1 and K2 */
    AVLTree node = singleRotateWithLeft(unbalancedNode.leftChild); //返回值为 K2 
    node.parent = unbalancedNode;
    /* Rotate between K3 and K2 */
    return singleRotateWithRight(unbalancedNode);  //最后返回的是 k2 结点，即根结点
}

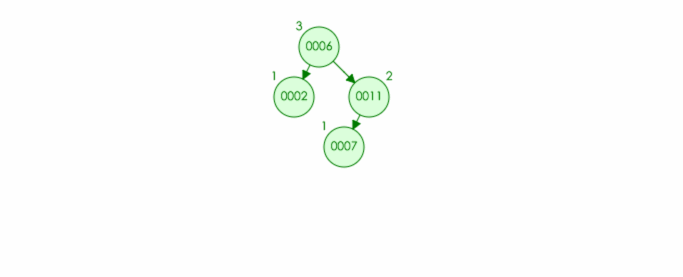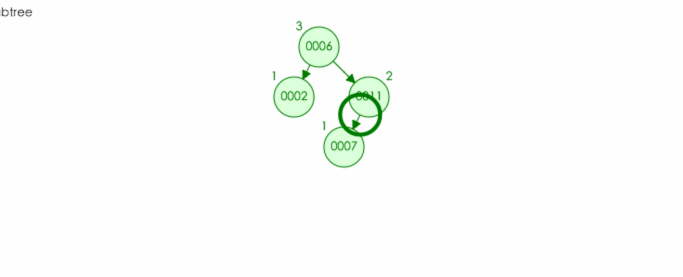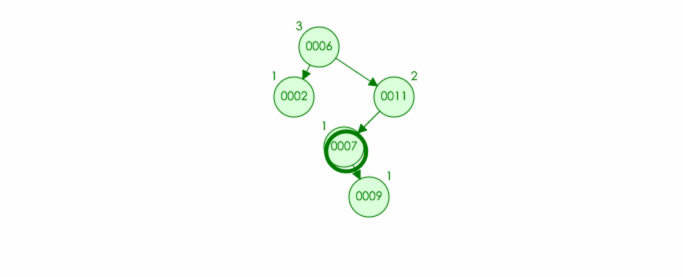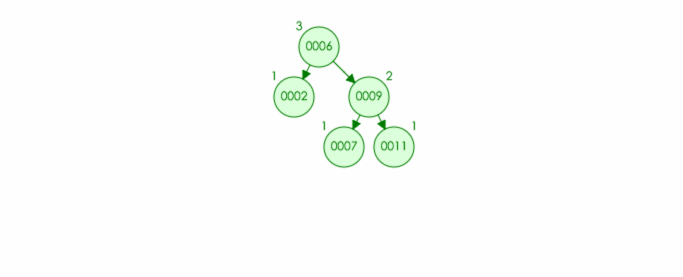
例如：往该树中插入结点 9

4.gif

情况3：对该结点的右儿子的左子树进行了一次插入。

类似需要旋转两次来达到平衡效果：

10.png

以 k3 为当前结点进行右旋，再以 k2 为当前结点进行左旋

代码实现:

public AVLTree doubleRotateWithLeft(PAVLNode unbalancedNode){   
    /* Rotate between K3 and K2 */
    AVLTree node = singleRotateWithRight(unbalancedNode.rightChild); //返回值为 K2 
    node.parent = unbalancedNode;
    /* Rotate between K1 and K2 */
    return singleRotateWithLeft(unbalancedNode);  //最后返回的是 k2 结点，即根结点
}

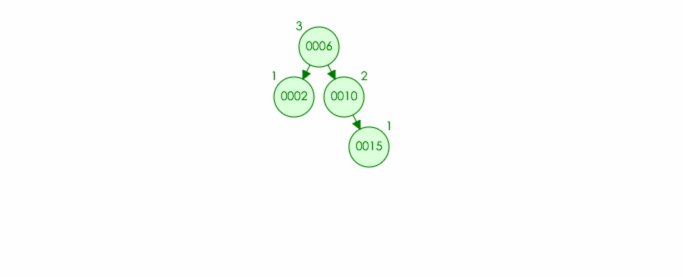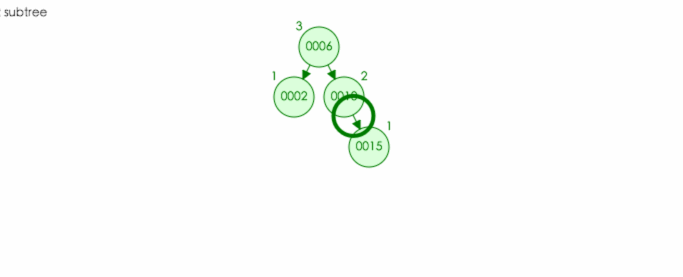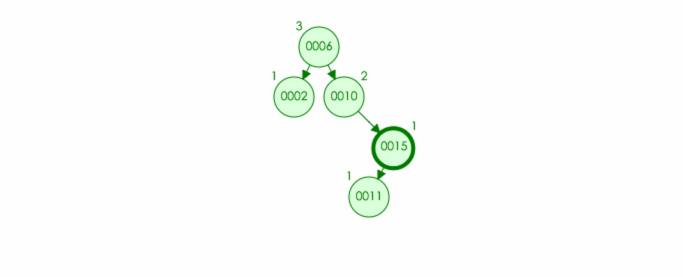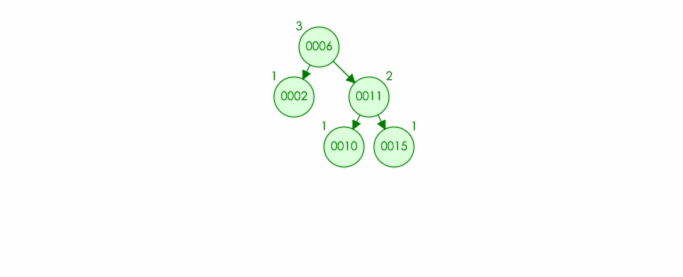
例如：往该树中插入结点 11

3.gif

插入操作：

插入的核心思路是通过递归找到合适的位置，插入新结点，然后看新结点是否平衡（平衡因子是否为2)，如果不平衡的话，就对其进行旋转操作：

在结点的左儿子(X < T->item):
在左儿子的左子树(X < T->l-> item): “外边”，要做单旋转。
在左儿子的右子树(X > T->l-> item): “内部”，要做双旋转。
在结点的右儿子(X > T->item):
在右儿子的左子树(X < T->r-> item)，“内部”，要做双旋转。
在右儿子的右子树(X > T->r-> item)，“外边”，要做单旋转。
(X == T->item) ，对该节点的计数进行更新。

课上的两个例题：构建一棵 AVL 树

往树中按顺序插入 342, 206, 444, 523, 607, 301, 142, 183, 102, 157, 149

5.gif

往树中按顺序插入 47, 23, 52, 14, 59, 29, 36, 38, 26

6.gif

参考链接：

数据结构之AVL树
AVL树 - 维基百科，自由的百科全书

4. 数据结构 － AVL 树