伸展树的引入:
我们知道AVL树为了保持严格的平衡,所以在数据插入上会呈现过多的旋转,影响了插入和删除的性能。从访问量上,我们知道许多应用场景都有一个“二八原则“,也就是说80%的人只会用到20%的数据,比如说我们的用的输入法,平常打的字也就那么多,或许还没有20%呢。右比如新闻消息,热门消息的访问量是远远大于普通消息的
伸展树的定义:
一种较为特殊的二叉查找树,特殊之处在于:** 当某个节点被访问时,伸展树辉通过旋转使该节点成为树根。这样能够使得下一次访问该节点时,能够迅速的访问到该节点。****
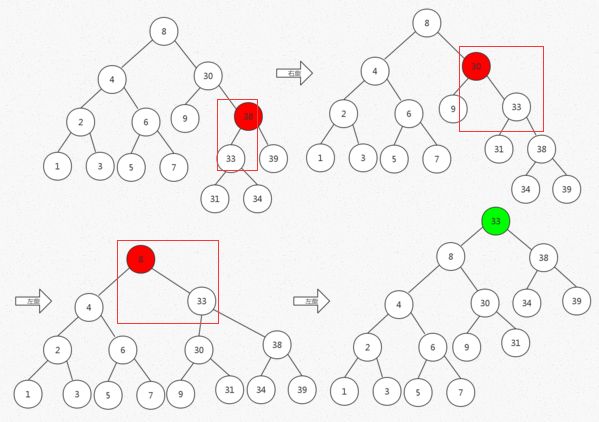
伸展树的实现:伸展即将某个节点旋转成为根节点,而实现的方法分为“自底向上”和“自顶向下”的方法。
a. 自底向上:首先找到目标节点的父节点,如果目标节点为父节点的左孩子,则进行右旋,如果目标节点为父节点的右孩子,则进行左旋转
如上图,红色节点表示为我们目标节点的父节点。
/** 比较--->查找目标节点--->对目标节点的父节点进行旋转
* 使用自底向上的方法实现伸展
* @param tree 节点
* @param data 目标值
* @return 返回目标节点
*/
public SplayTreeNode splay(SplayTreeNode tree, T data){
//若树为空,则返回
if (tree == null){
return null;
}
//进行比较
int result = mCompare(data, tree.data);
//小于0,说明目标节点在左子树
if (result < 0){
//在左子树中进行查找
tree.left = splay(tree.left, data);
//表示找到了目标节点,tree为目标节点的父节点,进行右旋
tree = rotationRight(tree);
}
// 大于0,说明目标节点在右子树
else if (result > 0){
//在右子树树种进行查找
tree.right = splay(tree.right, data);
//表示找到了目标节点,tree为目标节点的父节点,进行左旋
tree = rotationLeft(tree);
} else {
//找到目标节点,返回
return tree;
}
return tree;
}
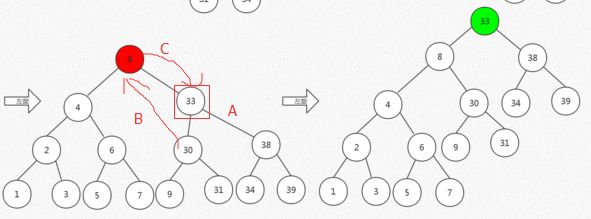
左旋:
A:表示找到目标节点
B:使目标节点的左孩子成为父节点的右孩子
C:使父节点成为目标节点的左孩子
/**
* 进行左旋转
* @param root 传入目标节点的父节点
* @return 返回以目标节点为根节点的部分树
*/
private SplayTreeNode rotationLeft(SplayTreeNode root) {
SplayTreeNode newRoot = root.right;//A
root.right = newRoot.left;//B
newRoot.left = root;//C
return newRoot;
}
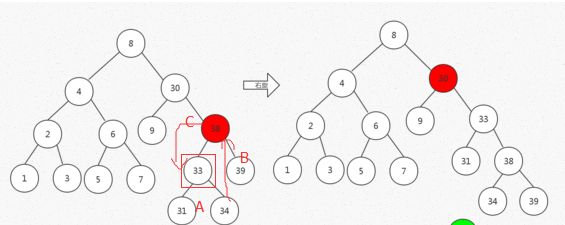
右旋:
A:找到目标节点
B:使目标节点的右孩子成为父节点的左孩子
C:使父节点成为目标节点的右孩子
/**
* 进行右旋
* @param tree
* @return
*/
private SplayTreeNode rotationRight(SplayTreeNode tree) {
SplayTreeNode newRoot = tree.left;//A
tree.left = newRoot.right;//B
newRoot.right = tree;//C
return newRoot;
}
实现具体的伸展:
(1)在查找时,进行伸展:
private SplayTreeNode search(SplayTreeNode tree, T data){
if (tree == null){
return null;
}
int result = mCompare(data, tree.data);
if (result < 0){
return search(tree.left, data);
} else if (result > 0){
return search(tree.right, data);
} else {
//找到目标节点,进行伸展,使其成为根节点
root = splay(root, data);
return tree;
}
}
(2) 在插入的时候进行伸展:
public SplayTreeNode insert(T data){
root = insert(root, data);
//进行伸展
root = splay(root, data);
return root;
}
(3) 在删除的时候进行伸展:
/**
* 删除时,进行伸展:
* a. 找到删除的节点
* b. 对删除的节点进行旋转,使其成为根节点
* c. 删除该节点后,问题是如何将左右子树进行拼接?
* (1) 若左子树不为空,则找到左子树中的最大值,因为左子树的最大值节点没有右子树
* (1.1) 将选中的最大值节点进行旋转,使其成为根节点
* (1.2) 将原来的右子树拼接过来
* (2) 若左子树为空,则右子树直接成为完整的树
* @param data
* @return
*/
public SplayTreeNode remove(T data){
SplayTreeNode newRoot, removeRoot;
if (root == null){
return null;
}
//找到要删除的节点
removeRoot = search(root, data);
//若没找到,则返回空
if (removeRoot == null){
return null;
}
//对要删除的节点旋转成为根节点
root = splay(root, data);
//左边不为空
if (root.left != null){
//找到左子树的最大节点值作为根节点,因为其没有右孩子存在
newRoot = splay(root.left, findMax(root.left).data);
//右子树直接赋值
newRoot.right = root.right;
}
//否则直接赋值右子树
else {
newRoot = root.right;
}
//更新树
root = newRoot;
//返回删除的节点
return removeRoot;
}
完整代码:
public class SplayTree> {
class SplayTreeNode>{
SplayTreeNode left;
SplayTreeNode right;
T data;
SplayTreeNode(SplayTreeNode left, SplayTreeNode right, T data){
this.left = left;
this.right = right;
this.data = data;
}
SplayTreeNode(){
this(null, null, null);
}
SplayTreeNode(T data){
this(null, null, data);
}
}
private SplayTreeNode root;
private Comparator cmp;
public SplayTree(){
root = null;
}
public SplayTree(Comparator cmp){
this.cmp = cmp;
}
private int mCompare(T a, T b){
if (cmp != null){
return cmp.compare(a,b);
}
return a.compareTo(b);
}
public SplayTreeNode insert(T data){
root = insert(root, data);
//进行伸展
root = splay(root, data);
return root;
}
private SplayTreeNode insert(SplayTreeNode tree, T data){
if (tree == null){
return new SplayTreeNode(data);
}
int result = mCompare(data, tree.data);
if (result < 0){
tree.left = insert(tree.left, data);
} else if (result > 0){
tree.right = insert(tree.right, data);
} else {
System.out.println("已经存在该值");
return null;
}
return tree;
}
private SplayTreeNode insert(SplayTreeNode rootTree, SplayTreeNode tempNode){
if (rootTree == null){
return tempNode;
} else {
int result = mCompare(tempNode.data, rootTree.data);
if (result < 0){
rootTree.left = insert(rootTree.left, tempNode);
} else if (result > 0){
rootTree.right = insert(rootTree.right, tempNode);
}
}
return rootTree;
}
public SplayTreeNode search(T data){
return search(root, data);
}
private SplayTreeNode search(SplayTreeNode tree, T data){
if (tree == null){
return null;
}
int result = mCompare(data, tree.data);
if (result < 0){
return search(tree.left, data);
} else if (result > 0){
return search(tree.right, data);
} else {
//找到目标节点,进行伸展,使其成为根节点
root = splay(root, data);
return tree;
}
}
public T getRoot(){
return root != null ? root.data : null;
}
public T findMax(){
return findMax(root).data;
}
private SplayTreeNode findMax(SplayTreeNode tree){
if (tree == null){
return null;
}
while (tree.right != null){
tree = tree.right;
}
return tree;
}
/**
* 删除时,进行伸展:
* a. 找到删除的节点
* b. 对删除的节点进行旋转,使其成为根节点
* c. 删除该节点后,问题是如何将左右子树进行拼接?
* (1) 若左子树不为空,则找到左子树中的最大值,因为左子树的最大值节点没有右子树
* (1.1) 将选中的最大值节点进行旋转,使其成为根节点
* (1.2) 将原来的右子树拼接过来
* (2) 若左子树为空,则右子树直接成为完整的树
* @param data
* @return
*/
public SplayTreeNode remove(T data){
SplayTreeNode newRoot, removeRoot;
if (root == null){
return null;
}
//找到要删除的节点
removeRoot = search(root, data);
//若没找到,则返回空
if (removeRoot == null){
return null;
}
//对要删除的节点旋转成为根节点
root = splay(root, data);
//左边不为空
if (root.left != null){
//找到左子树的最大节点值作为根节点,因为其没有右孩子存在
newRoot = splay(root.left, findMax(root.left).data);
//右子树直接赋值
newRoot.right = root.right;
}
//否则直接赋值右子树
else {
newRoot = root.right;
}
//更新树
root = newRoot;
//返回删除的节点
return removeRoot;
}
/**
* 使用自底向上的方法实现伸展
* @param tree 节点
* @param data 目标值
* @return 返回目标节点
*/
public SplayTreeNode splay(SplayTreeNode tree, T data){
//若树为空,则返回
if (tree == null){
return null;
}
//进行比较
int result = mCompare(data, tree.data);
//小于0,说明目标节点在左子树
if (result < 0){
//在左子树中进行查找
tree.left = splay(tree.left, data);
//表示找到了目标节点,tree为目标节点的父节点,进行右旋
tree = rotationRight(tree);
}
// 大于0,说明目标节点在右子树
else if (result > 0){
//在右子树树种进行查找
tree.right = splay(tree.right, data);
//表示找到了目标节点,tree为目标节点的父节点,进行左旋
tree = rotationLeft(tree);
} else {
//找到目标节点,返回
return tree;
}
return tree;
}
/**
* 进行左旋转
* @param root 传入目标节点的父节点
* @return 返回以目标节点为根节点的部分树
*/
private SplayTreeNode rotationLeft(SplayTreeNode root) {
SplayTreeNode newRoot = root.right;//A
root.right = newRoot.left;//B
newRoot.left = root;//C
return newRoot;
}
/**
* 进行右旋
* @param tree
* @return
*/
private SplayTreeNode rotationRight(SplayTreeNode tree) {
SplayTreeNode newRoot = tree.left;//A
tree.left = newRoot.right;//B
newRoot.right = tree;//C
return newRoot;
}
public void inOrder(){
inOrder(root);
}
private void inOrder(SplayTreeNode tree){
if (tree != null){
inOrder(tree.left);
System.out.print(tree.data + " ");
inOrder(tree.right);
}
}
}
测试代码:
public class SplayTreeTest {
public static void main(String[] args){
int arr[] = {8,4,30,2,6,9,38,1,3,5,7,33,39,31,34};
SplayTree splayTree = new SplayTree();
//进行插入
for (int anArr : arr) {
splayTree.insert(anArr);
}
//打印树
System.out.println("root:" + splayTree.getRoot());
printArr(splayTree);
//进行搜索节点33
splayTree.search(33);
System.out.println("root:" + splayTree.getRoot());
printArr(splayTree);
//进行删除节点8
splayTree.remove(8);
System.out.println("root:" + splayTree.getRoot());
printArr(splayTree);
}
private static void printArr(SplayTree splayTree){
System.out.println("当前树的中序遍历如下:");
splayTree.inOrder();
System.out.println();
}
}
实现结果:
root:34
当前树的中序遍历如下:
1 2 3 4 5 6 7 8 9 30 31 33 34 38 39
root:33
当前树的中序遍历如下:
1 2 3 4 5 6 7 8 9 30 31 33 34 38 39
root:7
当前树的中序遍历如下:
1 2 3 4 5 6 7 9 30 31 33 34 38 39