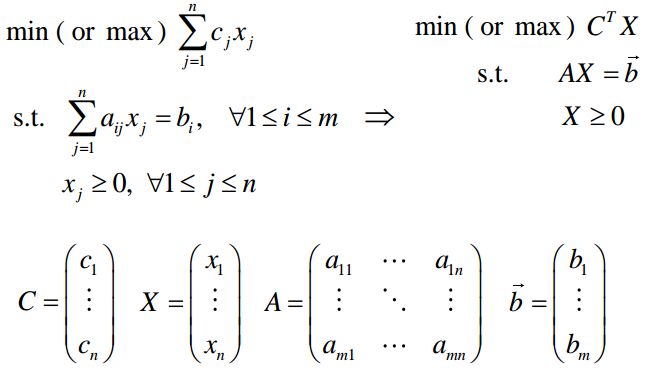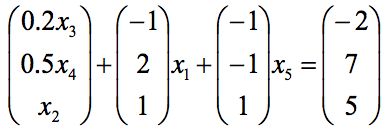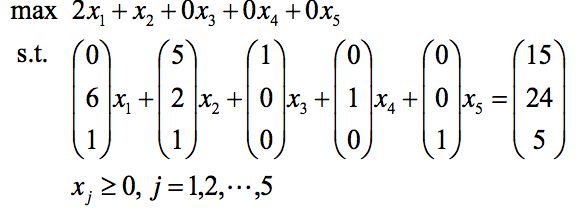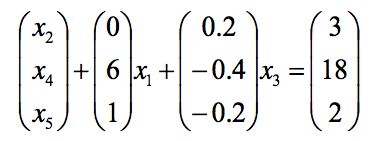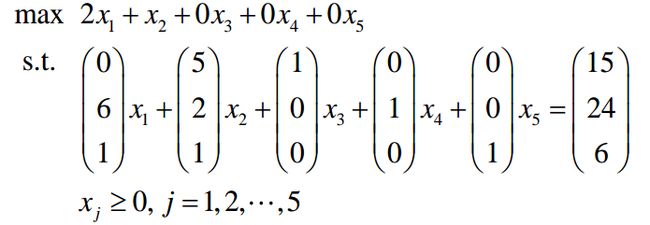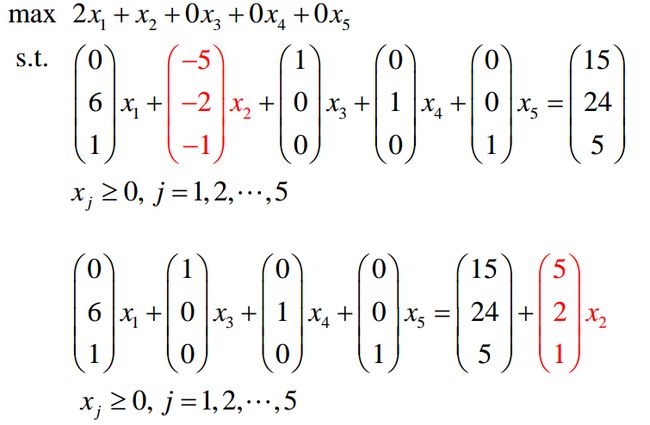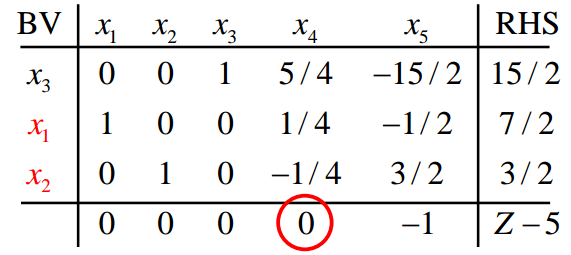转载请注明出处 http://www.jianshu.com/p/dd0761a2fdfd
作者:@贰拾贰画生
单纯形法应用于求解线性规划(LP)问题中最优解。其主要思想是,沿着可行解区域的边界走,从一个点跳到另一个点,直到找到最优解。
一. 详述单纯形法
单纯形法应用在线性规划的标准模型上,任何一个线性规划的一般形式都可以化为标准模型。
线性规划模型的一般形式为:
把它转换为标准型是要求所有的约束都是等式约束,且所有的决策变量非负。
如下面的形式:
举个例子:
那么很容易就可以写出这个线性规划问题的数学模型:
这是一般形式,我们转换为标准型:
是的,我们增加了三个变量x3, x4, x5。这样就把不等式约束变成了等式约束,且决策变量都非负。
再重复一遍,线性规划的标准型必为以下形式:
它有三个基本要素: 1. 一个明确的目标函数;2. 等式约束; 3. 决策变量非负。
对于标准型我们有两个基本假设:
1. 系数矩阵A的行向量线性无关。
2. 系数矩阵A的列数大于其行数,即n>m。因为如果n
回到刚才那个例子,我们可以将找个标准型写为如下形式:
这个例子m = 3, n = 5。那么我们可以用三个变量表示所有的五个变量,这三个变量我们称之为基变量。上图中,x3, x4, x5的系数是一个单位阵。我们把这种形式的等式约束称为典式。
观察这个典式,我们可以很容易的看出其一个基本可行解:(0, 0, 15, 24, 5)T,即非基变量等于0,基变量等于等式右边的常数。这个解,我们可以把它想象成基本可行解区域的一个顶点,我们知道最优解也在顶点上,那么我们只要沿着边界找这个最优顶点就可以了。
对于顶点(0, 0, 15, 24, 5)T,它的x3, x4, x5是基变量,那么与该顶点相邻的其他顶点的基变量有什么关系呢?事实上,与之相邻的顶点的所有基变量中只有一个基变量发生了变化。这是可以验证的。所以,接下来的工作就是从x1, x2中选一个非基变量进基成为基变量,从x3, x4, x5中选一个基变量出基成为非基变量。
那么问题来了,我们怎么选择进基变量和出基变量?
假设我们想要x2进基,那么根据基本可行解的表示式,我们必须通过初等行变换的形式让x2只出现在一个等式约束中,就是把x2的系数变成(1,0,0)T或(0,1,0)T或(0,0,1)T的形式。
假设我们把x2变成(0,0,1)T的形式,初等行变换后得到:
我们发现等式右边的常数有一个变成负数-2,这是不可以的,因为我们知道决策变量有非负约束。所以,在选择进行初等行变换时,应注意选择(右边常数/进基变量系数)最小的那一行。这个例子中,x2进基,15/5 = 3, 24/2 = 12, 5/1=5,3最小,那么将x2系数转换为(1,0,0)T的形式,与此同时,出基变量也就确定了那就是x3。所以,我们得到:
其基本可行解为(0,3,0,18,2)T。
若此时,我们又想让x3进基,应当注意只能将其系数化为(1,0,0)T的形式,因为x3第二行与第三行的系数都为负数,若保留此两行会将右边的常数变成负数。 所以,只能保留进基变量系数的非负行。
现在对于例子
我们得到了两个基本可行解X1 = (0,0,15,24,5)T, X2 = (0,3,0,18,2)T,记目标函数f(X) = 2x1 + x2 + 0x3 + 0x4 + 0x5
则f(X1) = 0, f(X2) = 3
那么我们怎么找到最优解呢?
我们知道 X2 = (0,3,0,18,2)T 的约束的表示式为:
从这个表示式中我们可以得到基变量和非基变量的函数关系,将这个函数关系带入到f(X) = 2x1 + x2 + 0x3 + 0x4 + 0x5中,就得到
f(X) = 3 + 2x1 - 0.2x3 = f(X2) + 2x1 - 0.2x3,(只保留非基变量x1,x3)
发现什么没有?
对于可行解X2 = (0,3,0,18,2)T,x1,x3是非基变量啊,非基变量是0啊。但是,我们下一步不是选择进基变量吗,进基变量不是从非基变量里选吗,我们选x1啊,为啥?x1的系数是正数2啊!我们这个例子是求z的最大值,如果x1进基,那么必然会让f(X)增大,因为我们的决策变量都是正数,正数乘正数还是正数,增量肯定是大于0的。我们看到x3的系数是-0.2,如果让x3进基的话,增量肯定是小于0的。
如果x1, x3的系数都大于0怎么办?那随便选啊。
如果x1,x3的系数都小于0怎么办?哈哈,有人可能就意识到了,非基变量的系数都小于0,选谁进基都会造成f(X)变小,我们不是求最大吗?那我们谁也不选啊,这个问题已经结束了,我们已经找到最优解了!
所以,选择进基变量的问题,以及判断找到最优解的问题就都解决了。
我们一般使用单纯形表来直观表示这个过程。
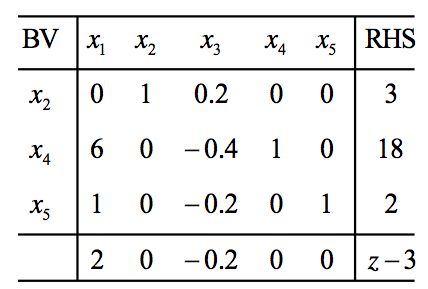
还是可行解X2 = (0,3,0,18,2)T,它对应的单纯形表如下:
最左边一列是基变量,最右边一列是约束右边的常数项,中间一坨是决策变量的系数。最下边一行是目标函数z = 2x1 + x2 + 0x3 + 0x4 + 0x5。最下面一行决策变量的系数我们称之为检验数。
我们通过行变换将最后一行的基变量前面系数变成0,就得到下面的单纯形表:
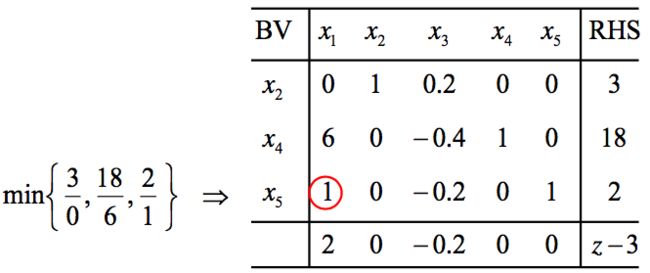
我们称之为X2的单纯形表。利用这个表,我们可以很容易的获得让x1进基后的基本可行解的单纯形表,先确定让x5出基。
然后通过行变换将x1所在列除了第三行以外的系数变成0,就可得到新的基本可行解对应的单纯形表:
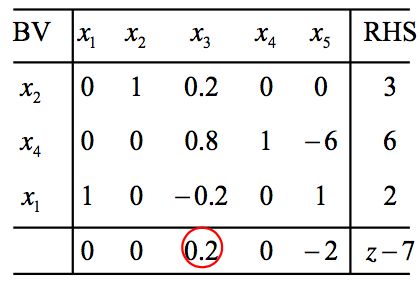
从这个表中我们可以得到以下信息:
- X3 = (2,3,0,6,0)T是基本可行解;
- X3的目标函数值是z=7;
- x3的检验数大于0,让x3进基能够增加目标函数值。
然后通过刚才的方法让x3进基,得到新的基本可行解的单纯形表:
从这个表我们可以得知:
- X4 = (3.5,1.5,7.5,0,0)T是基本可行解;
- X4的目标函数值是z=8.5;
- 非基变量的的检验数都小于0,任何非基变量进基都不能使目标函数值增加。
至此,我们已经得到该问题的最优解X4。
二. 几种特殊情况
1. 退化问题
我们知道,对于一个基本可行解,一般情况下它的基变量是大于0,非基变量等于0。退化情况是,我们有一个基变量也等于0。那么,这个基本可行解就会对应于多个可行基阵。
举个例子:
X = (3,3,0,0,0)T是该问题的可行解
我们可以令x3,x4为非基变量, 也可以令x3,x5或x4,x5为非基变量。
退化情况存在的问题在于,经过一次进出基迭代后得到的是同一个基本可行解,因此有可能出现迭代算法在一个基本可行解的几个基矩阵之间循环不止的情况。
所以,保证单纯形法收敛的充分条件是:在迭代过程中产生的每个基本可行解的基变量数值都严格大于0。
2. 如果xj的系数都小于0
在迭代过程中,如果某一个决策变量的系数都小于0了,这代表什么?
举例:
如上图,我们可以把x2放在等式右边,看出什么没有?x2可以趋于无穷大。
3. 如果非基变量xj的检验数为0
如上图, 非基变量x4的检验数为0了,根据最优性条件,让其进基并不能继续优化目标函数值。但是,x4进基后还是会得到一个基本可行解,且目标函数值与当前结果相同。这意味这什么?
目标不能再优化,但是又有不同的基本可行解,啥意思?说明该问题有无穷多个最优解。
所以,对于求max的线性规划问题,如果所有检验数均满足<=0,则说明已经得到了最优解,若此时某非基变量的检验数=0,则说明该优化问题有无穷多最优解。
三. 如何确定初始基本可行解
单纯形法是从一个初始的基本可行解开始的,出基入基,知道找到最优可行解。
问题是,我们怎么得到那个初始的基本可行解啊?
最基本的方法是添加人工变量
假设原问题的约束是这样的:
x1 + 2x2 + 3x3 = 1
2x + x3 = 2
那么我们再加两个变量x4, x5,把约束变成这样:
x1 + 2x2 + 3x3 + x4 = 1
2x + x3 + x5 = 2
我们就把约束变成了典式,可以直接得到一个基本可行解(0,0,0,1,2)T,找个基本可行解的基变量是x4, x5,那么接下来的工作就是通过出基入基把x4,x5都变成非基变量,这样它们的值就可以为0, 从而得到原问题的可行解。
现在有个问题,如果在最优表中,基变量中仍含有人工变量,这说明啥?
这说明,原问题根本就无解。