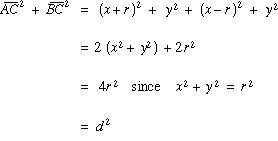π的历史简介
众所周知,π=3.141592653…可以说,它是世界上最有名的无理常数了,代表的是一个圆的周长与直径之比或称为“圆周率”。公元前250年左右,阿基米德给出了“圆周率”的估计值在223/71~22/7之间,也即是在3.140845~3.142857之间。
中国南北朝时期的著名数学家祖冲之(429-500)首次将“圆周率”精算到小数第七位,即在3.1415926和3.1415927之间,他提出的“密率与约率”对数学的研究有重大贡献。直到15世纪,阿拉伯数学家阿尔·卡西才以“精确到小数点后17位”打破了这一纪录。
代表“圆周率”的字母π是第十六个希腊字母的小写。也是希腊语 περιφρεια(表示周边,地域,圆周)的首字母。1706年英国数学家威廉·琼斯(William Jones, 1675-1749)最先使用“π”来表示圆周率。1736年,瑞士数学家欧拉(Leonhard Euler, 1707-1783)也开始用表示圆周率。从此,π便成了圆周率的代名词。
π为什么是常数?
介绍完一些关于π的来历后,我准备着手沿着古人的方式去寻找π,但此时我发现忽略了一个重要的前提条件——为什么π是一个常数?即为什么所有圆的周长和直径之比为一个定值,这一点似乎并不能够自然而然地就得到。因此在寻找这个常数之前,先要做的应当是证明“圆的周长与直径之比确实是一个常数”。
如上图所示,以点O为圆心作两个半径不同的圆,小圆的半径为r1,周长为c1;大圆的半径为r2,周长为c2。分别作两个圆的内接正n边形(n为偶数),边长分别为k1和k2,且保证正两个n边形过圆心的对角线重合。
那么有OA:OD=OB:OC,∠AOB=∠COD,因此△OAB∽△OCD。
所以有k1/r1=k2/r2。
设小正n边形和大正n边形的周长分别为c1’和c2’,则有c1’=nk1,c2’=nk2。
所以有c1’/r1=c2’/r2。
由于当n→∞时,c1’=c1,c2’=c2,即取极限或者说是逼近的思想,当边数区域无穷,内接多边形就近似是一个圆了,后面寻找π时还会再次用到这个思想。
所以就有c1/r1=c2/r2,表示的是:对于半径不同的圆,其各自周长与半径的比为定值,或者说为常数,记该常数为2π,则圆的周长与直径之比为π,当然也是一个常数,证明完毕。
好,既然圆的周长和直径之比是一个常数,下一步要做的就是去寻找这个常数或它的近似值了。
我们可以从书中、从网上、从各种我们能够想到的渠道获得这个神奇的常数。不过,如果只给你一支笔、一张纸,你能否找到它的近似值呢?
阿基米德的智慧
阿基米德(Archimedes, 287-212 BC) 在2200多年前就已经通过计算得到了精度高达99.9%的π,在他那个年代还没有定义小数,甚至连“0”的定义都没有(相传“0”是到了公元5世纪才由印度人最先用于计算之中),那么他当年是怎么计算π的呢?
在得到圆周率之前,阿基米德当然无法知道一个圆的周长,但是他可以从他知道的开始,比如正方形(实际上他用的是正六边形,为了演示方便,这里从正方形开始)。
对于上图中一个已知直径为1的单位圆(其周长即为π),可以以其直径为边长作出其外切正方形,也可以以其直径为对角线作出其内接正方形。不管圆的周长是多少,其总满足大于内接正方形的周长,小于外切正方形的周长。
外切正方形周长:
P4=1×4=4
内接正方形周长根据勾股定理有:
p4≈0.7×4=2.8
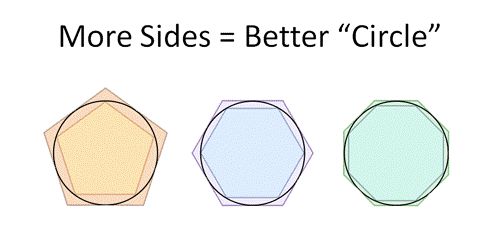
假设现在π的大小未知,我们只能肯定π在2.8到4之间,先取个中间值作为π的估计值,约等于3.4。我们发现这样精度很低,因为用4边形来估算实在是太“粗糙”了,为了提高这种方法的精度,可以用边数更多的正多边形来逼近。
可以看出,到了正八边形时,内接八边形与外切八边形之间的“间隙”比正方形的情况小了。此时π的估算值相对于正方形的情况会有一个精度上的提升。但是,现在的问题是:八边形的周长如何计算?而且就算把八边形的周长计算出来了,那16边形、32边形岂不是精度更高,那又该怎么计算?
正多边形逼近
下面需要用到两条基本定理:
定理一:半圆的内接三角形为直角三角形,且直角顶点在圆周上。
定理二:圆的弦所对应的圆周角为其所对应的圆心角的一半。
定理一的证明,证明半圆的内接三角形为直角三角形:
对于上图,令半径为r的半圆圆心在坐标原点,三角形的一边为半圆直径,一个顶点C在半圆的圆周上,坐标为(x,y)。
则有:
根据勾股定理可知,∠ACB为90°。
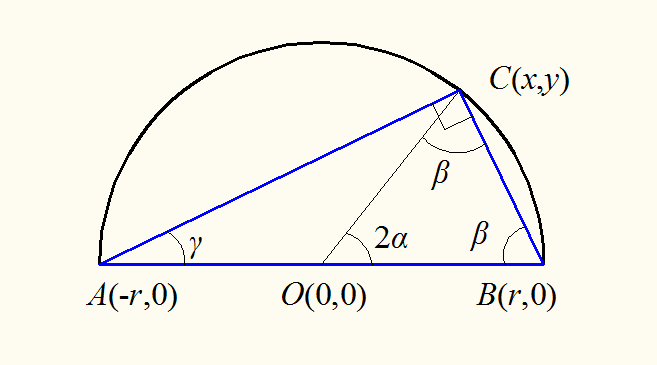
定理二的证明:即“圆上同一根弦所对应的圆周角为圆心角的一半”,可以用下图证明:
对于△OBC,因为OB=OC,有β+β+2α=2β+2α=180°;对于△ABC,由定理一知: ∠ACB=90°,有:β+90°+γ=180°,即β+γ=90°,因此有γ=α。即圆上的一条弦所对应的圆周角是其所对应圆心角的一半。
对于内接多边形:
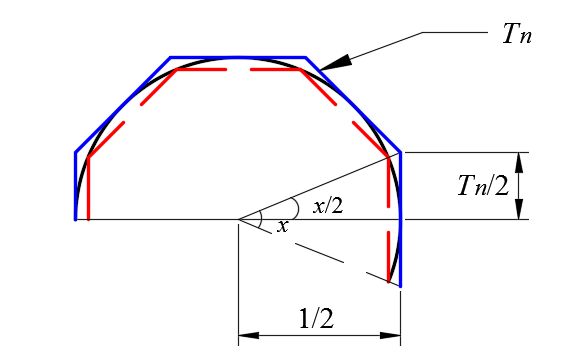
如下图所示,设内接多边形的每个边的边长为Sn,每个边对应的圆心角为x。
根据定理一和二,可以得出,内接多边形的边长Sn=sin(x/2)。
对于外切多边形
如下图所示,易得,外切多边形的边长为Tn=tan(x/2)。
所以,对于正方形
单位圆内接正方形的周长为:
p4=4×sin[(360°/4)/2]= 2.8284271247
单位圆外切正方形的周长为:
P4=4×tan[(360°/4)/2]=4
而对于正八边形
单位圆内接正八边形的周长为:
p8=8×sin[(360°/8)/2]= 3.0614674589
单位圆外切正八边形的周长为:
P8=8×tan[(360°/8)/2]= 3.313708499
因此,对于正n边形
单位圆内接正n边形的周长为:
pn=n×sin[(360°/n)/2]
单位圆外切正n边形的周长为:
Pn=n×tan[(360°/n)/2]
对于我们来说,问题似乎已经解决了,只要n足够大,结果就会很精确,可以通过不停地增大n直到直达到想要的精度。
但是,又忽略了一个问题!阿基米德那个时代并没有计算器,不像今天,想算sin或者tan,So easy~只需要按几个键就行了。因此,直接用三角函数计算在当时其实是行不通的!
得换换思路了!
阿基米德迭代算法
阿基米德不愧是数学大师。为了解决这一棘手的问题,阿基米德发明了一种“迭代算法”:
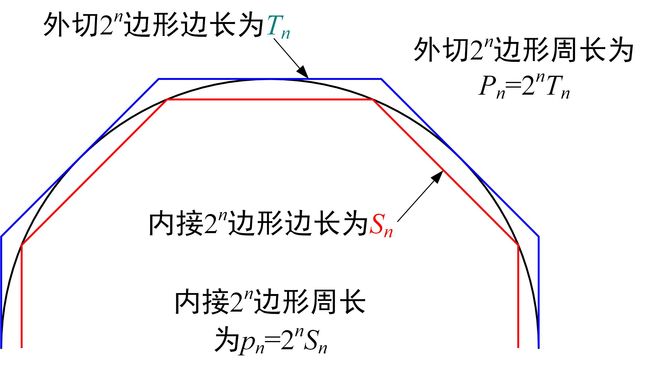
为了方便计算,将内接和外切多边形的边数定为2n个,n为整数,且n≥2,如下图所示。
内接2n边形的边长为Sn,则其周长为pn=2n·Sn;外切2n边形的边长为Tn,则其周长为Pn=2n·Tn。
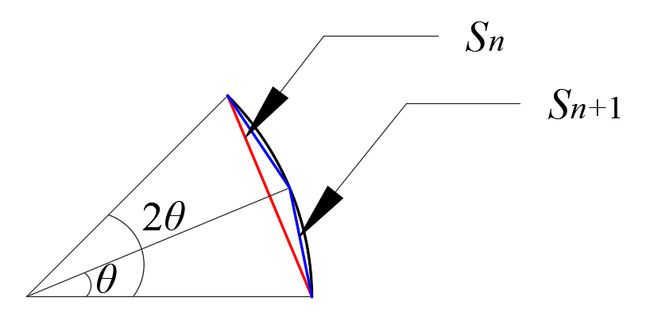
如果令正2n边形的边长所对应的圆心角为2θ,由上面的推导知:
内接正2n边形的边长Sn=sin(θ)
外切正2n边形的边长Tn=tan(θ)
那么,正2n+1边形的边长所对应圆心角为θ,由上面的推导知:
内接正2n+1边形的边长Sn+1=sin(θ/2)
外切正2n+1边形的边长Tn+1=tan(θ/2)
有以下递推公式:
由此,可以计算外切正2n+1边形的周长Pn+1:
以及内接正2n+1边形的周长pn+1:
即:
可以注意到的是:
Pn+1是pn与Pn的“调和平均数”;
pn+1是pn与Pn+1的“几何平均数”。
通过这样的递推公式,可以直接以内接及外切正2n边形的周长来计算内接及外切正2n+1边形的周长,成功避免了三角函数的引入。
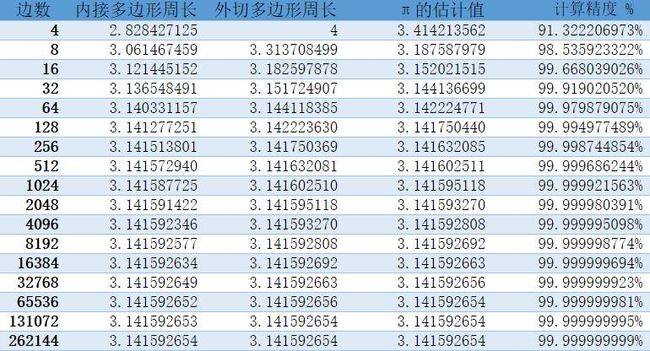
通过递推公式,可以计算得到以下结果:
可以看出,当正多边形的边数到达64时,已经有了不错的精度,而阿基米德当年用的是正六边形,方法是一样的,他计算了正12边形、正24边形、正48边形和正96边形。那他为什么没有继续算下去?
前面已经说了,公元前250年人们还没有发明小数,人们只能用分数来近似各个根号项所得到的无理数,当近似项增多,误差就会随之增大,在这种情况下,阿基米德算到了正96边形,得到π的值在223/71~22/7之间,计算精度达到了99.9%,在那个时代已经是很高的精度了。
所以在其后的很长一段时间里,人们用22/7来近似圆周率,取的正是阿基米德计算结果所在区间的上界。
中国人的贡献
不过,后面有人发现了一个神秘的分数:355/113,其精度居然达到了99.99999%,而发现这个数的人正是中国南北朝时期数学家祖冲之。时间大概在公元480年左右。他给出了两个分数:密率355/113和约率22/7。顾名思义就是密率精度高,约率的精度稍低一些。
密率355/113是一个很好的分数近似值,因为至少要取到52163/16604才能够比密率的精度更高一点,但这样的分数就显得不太实用了。完美主义者可能会纠结于没有找到精确的π,但要知道,发现π是一个永远都不会停止的过程,这也是其魅力之所在。没有最精确,只有更精确。
寻找π的过程就是这样神奇,一开始它的模型看起来很“粗糙”,随着边数的增多,边长的细化,计算结果越发逼近理想值,其实这就是“微积分”思想的雏形。而且有意思的是,微积分的出现最后又导致了很多更好的计算π的公式的出现。
Reference
[1]Archimedes
https://en.wikipedia.org/wiki/Archimedes
[2]Zu Chongzhi
https://en.wikipedia.org/wiki/Zu_Chongzhi
[3]Prehistoric Calculus: Discovering Pi
https://betterexplained.com/articles/prehistoric-calculus-discovering-pi/