1.学习总结
1.1树结构思维导图
1.2 树结构学习体会
谈谈你对树结构认识,学习这个结构是否遇到哪些困难,树结构可以解决的问题。
树是一种十分重要的非线性数据结构,有一对多的结构特点。
困难 树结构在编程中较抽象,出现过一些理解的困难。对数结构的应用较生涩。
可以解决的问题:堆及其应用,哈夫曼树,集合及其运算。
2.PTA实验作业
本周要求挑选出3道题目书写设计思路、调试过程。设计思路使用伪代码描述。题目选做要求:
- 如果选6-1,只需要描述建树的伪代码。
- 6-4必选
具体书写内容及格式如下:
2.1 题目1:
6-2 求二叉树高度
2.2 设计思路(伪代码或流程图)
int GetHeight( BinTree BT )定义left左子树高度,定义right右子树高度
left=right=0;
if(空树) return 0;
left= GetHight(左子树);
right=Getheight(右子树);
if(左子树比右子树高) return left+1;
否则 return right+1;
2.3 代码截图
2.4 PTA提交列表说明。
编译错误因为Bintree定义Left,Right首字母大写,提交的时候没有大写。
题目2:
6-4 jmu-ds-表达式树
2.2 设计思路
void InitExpTree(BTree &T,string str)
{
stack a 存放数字,x 存放运算符;
while(str还有元素)
if(str【i】不是运算符) 新建树类型节点将该元素存入栈a;
else {
switch(比较x.top和str[i])
{
case‘小于’ :x.push(str【i】)
case‘等于’:x出栈
case‘大于’:新建T节点,T.data为x栈顶,T右孩子为a栈顶,a出栈将T压入栈,x出栈,T左孩子为a栈顶,a出栈后压入T,x出栈
}
}
while(x栈顶不为‘#’){
新建T节点,T.data为x栈顶,T右孩子为a栈顶,a出栈
if(a不为空)T左孩子为a栈顶,a出栈
将T压入a,x出栈
}
T为a栈顶。
}
double EvaluateExTree(BTree T)
{
定义a,b分别代表左右子树的值
if(T为根节点)return T.data;
递归算法a=EvaluateExTree(T左子树) b=EvaluateExTree(T右子树)
switch(T。data){
case‘+ - *’ return a + - *b;
case‘/’ if(b为0)输入提示 程序非正常终止
else return a/b;
}
}
2.3 代码截图
2.4 PTA提交列表说明。
建树的时候对左孩子赋值没有处理好
题目3:
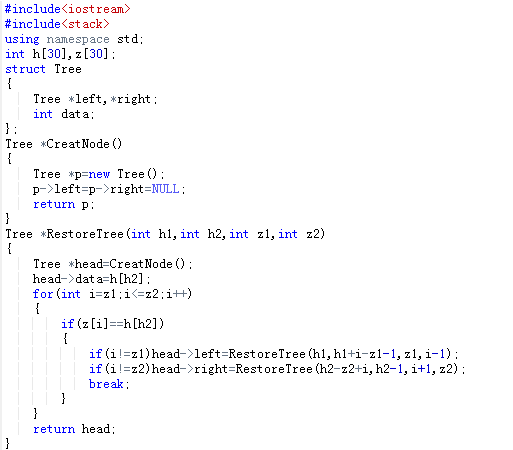
7-2 根据后序和中序遍历输出先序遍历
2.2 设计思路
Tree *RestoreTree(int h1,int h2,int z1,int z2) h为后序序列,z为中序序列,h1h2z1z1分别代表两序列的首末下标
{
新建head节点;
head.data=后序序列末元素h【h2】;
for(int i from 首下标 to 末下标)
{
if(z【i】等于根){递归RestoreTree建立左右子树}
}
}
先序遍历head展示结果 void PreOrder(Tree *tree)
2.3 代码截图
2.4 PTA提交列表说明。
输出格式空格间距问题
3.截图本周题目集的PTA最后排名
总分:1分
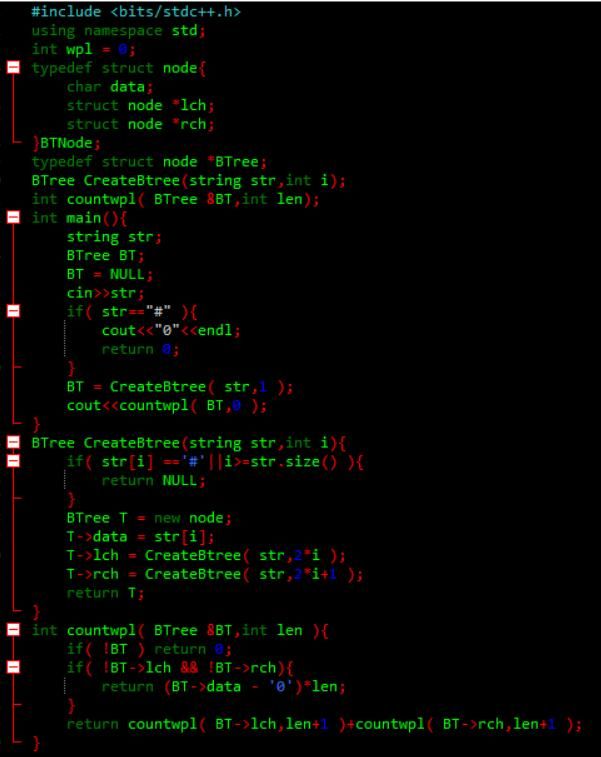
4. 阅读代码(必做)
代码功能为计算叶子节点带全路径。优点利用字符串层次遍历的特点理清了元素i和左孩子2i右孩子2i+1的关系,方便了树的构造和带权路径长度计算。
地址:http://www.cnblogs.com/lanxiang/p/8995779.html