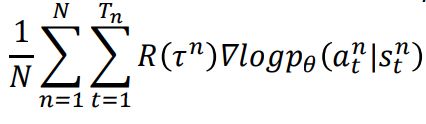邂逅黑科技之强化学习(二)：Policy Gradient

承上，首先是Policy Based经典算法，基础的Policy Gradient以及它的进化版PPO等，下面内容主要参考李宏毅老湿的讲义与口述：

Policy Gradient

算法动机

在深度强化学习中，Policy \pi可以看做是一个参数为\Theta的神经网络，以打游戏的例子来说，输入当前的状态（图像），输出可能的action的概率分布，选择概率最大的一个action作为要执行的操作：

policy.png

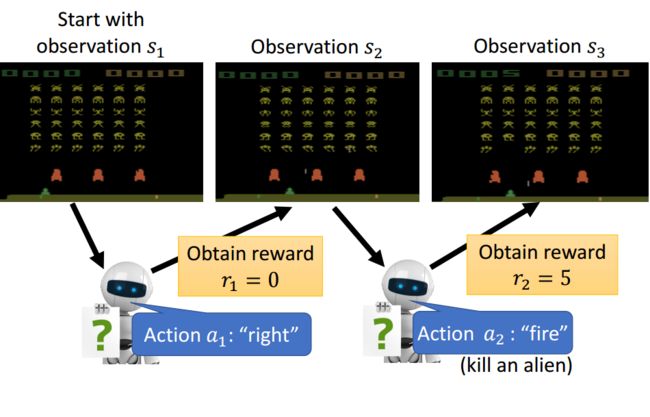
还是以打蜜蜂的游戏为例（好像是打外星飞船），Actor(神经网络)看到一副游戏画面，输出相应的aciton，根据游戏规则或者其他规定会得到相应的reward：

play game

从游戏开始到结束（消灭了所有的外星人或者挂掉），叫做一个episode，简单理解为回合。episode结束，游戏过程中所有的reward相加得到该回合的总reward（挂与未挂可能是一个负reward或一个大的正reward）。

totle reword

这里强化学习的目标就是学习一个Policy，即一个网络，使其每看到一个画面，做出一个action, 并做到最终获得最大总reward。

算法细节

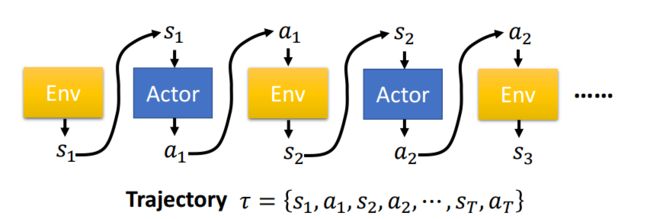
游戏的进程相应的可以表示成state,action交替的序列:

image.png

游戏引擎（Environment）产生一个画面（state）,接着神经网络玩家（Actor）产生一个action，接着影响Environment，并产生下一个state，如此反复到游戏结束，一个完整的序列（1-T）为一个Trajectory，可以理解为t时刻分别为s_t和a_t的一轮游戏，或者叫一轮采样。同样可以有该序列发生的概率，即在策略\pi的参数为\theta情况下Trajectory \tau发生的概率：

p

这样在此Trajectory下会得到一个总的回报R(\tau)，可以想到，玩游戏有很大的随机性，不同的action就可能会有不同的state，反之亦然。因此R(\tau)实际是一个变量（根据游戏场景过程的变化而变化），因此为了衡量一个策略\pi的好坏，需要考虑一个期望的回报R_E(\tau)。游戏的过程当然也不可能穷举，因此就需要采样来计算期望回报（“平均”回报），可以理解为Policy固定情况下反复的试玩N回合游戏，每回合的reward以回合发生概率为权重相加取平均，即为当前策略的期望reward。目标也就是不断更新Policy的参数\theta，使期望reward得到最大。

image.png

Policy Gradient

有了目标，下面就是用合适的方法，使期望reward最大，一种方法便是策略梯度提升的方法（与最小化loss的梯度下降相对）。由上面可知期望reward是参数\theta的函数，所以参数更新的方式为：

image.png

下面的问题就是期望reward对\theta的导数的求法，走一波公式推导：

image.png

公式推导并不复杂，主要是蓝框里的一个常用小技巧变换（同时乘和除f(x)）。然后第二行等式到第三行将累加转换为期望表示；接着约等于N次采样的期望值。第三行到第四行将上面的p_{\theta}(\tau)带入，去掉与\theta无关的环境相关概率p(s_{t+1}|s_t, a_t)和p(s_1),得到最终结果：

image.png

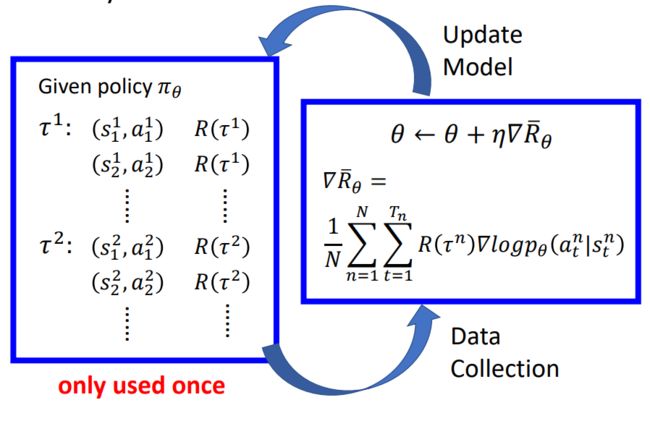
下面就是不断采样，更新参数的过程（根据当前策略玩游戏，得回报，修正策略）：

image.png

图示左边表示根据当前policy参数采样得到N个Trajectory，计算一次期望reward，然后梯度上升的方法更新policy参数，用更新后的policy再进行下一轮采样，如此往复直到收敛，得到期望reward最大的policy。最终该policy（神经网络表示）就学会了根据游戏画面做合适的action，最终赢得游戏。

实现

道理是这个道理，具体实现过程中还是有几点可说，得到一波采样序列如何去train当前的神经网络。可以将其看作一个分类问题，网络输入图像，输出可能的action的概率分布，求目标函数，做反向传播。目标函数也可以理解为，用采样的到的action做神经网络的target，求交叉熵做目标函数，不同的是目标函数要加入reward。

image.png

另外现在的目标函数仍存在一定问题，在具体实现过程中有下面几个tips:

Tip1

考虑有一些游戏或者其他的情况，reward总是正，这种情况下做梯度提升，参数总是在增加，或者说当前策略的采取每个action的概率都在提升。虽然想想也不是不可以，虽然概率都是增加，但总还是有大有小，还是可以区别好的action和不好的。但是，注意目标函数是通过采样计算得到的，如果考虑到不幸的情况，有的action，虽然比其他的好，但是就是没被采样到，这种情况下其他的bad action因为被采样到提升了出现的概率，对没被采样到的action就缺少公平性了。

解决这个问题的一个可行方法便是给引入一个基准，给采样获得的reward做一个偏差，使reward有正有负，这个基准一般选择采样reward的平均值。

image.png

Tip2

之前计算的R(\tau^n)是在第n回合结束的总reward，也就是说，该回合的采取的action都对应着同一个奖励回报，这样有些时候确实也是不合理的：因为，最后的结果坏不一定是每个action都不好，最后得到高回报也不一定是每个action都好。

从这个角度出发，思考怎么修正目标函数，改R(\tau^n)为：

image.png

即在当前时刻采取一个action，仅考虑当前t时刻之后的reward之和。换种说法就是当前时刻采样的action只对当前时刻之后的回报有影响。

更进一步，当前时间点t采取的action只对近期的reward影响比较大，而随着时间的推移，对后面的reward影响会越来越小（游戏开始采取的action,对最后的reward影响一般比较小）。因此，给后面时刻获得的reward进行相应的折扣也就变得合理。

最终，目标函数进化成这个模样：

image.png

到此，初版Policy Gradient打完收工！

转载求注明出处

参考资料：

李宏毅深度强化学习
Deep Reinforcement Learning:Proximal Policy Optimization (PPO)

更多关注公众号：

wechat