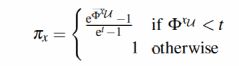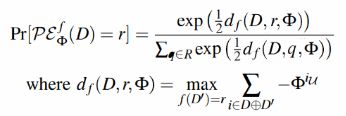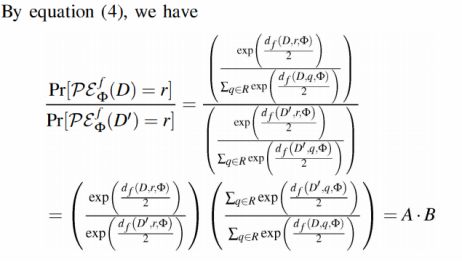Conservative or Liberal? Personalized Differential Privacy
保守或自由?个性化的微分隐私
Abstract-差异隐私被广泛接受为为聚合数据分析提供强有力的正式隐私保证的强大框架。该模型的一个限制是,所有个人都享有同等程度的隐私保护。然而,数据主体对其数据的可接受的隐私水平有不同的期望,这是很常见的。因此,差别隐私可能会导致一些用户的隐私保护不足,而过度保护其他用户。我们认为,通过接受并非所有用户都需要相同级别的隐私,通常可以通过不向不想要隐私的用户提供过多的隐私来获得更高级别的实用价值。我们提出了一种新的隐私定义,称为“个性化差异隐私”(P(personalized)DP),这是一种对差异隐私的推广,其中用户为其数据指定了个人隐私需求。然后介绍了几种实现PDP的新机制。我们的主要机制是一个通用机制,可以自动将任何现有的差异私有算法转换成满足PDP的算法。受著名的指数机制的启发,我们还提出了一种更直接的实现PDP的方法。我们通过在真实和合成数据上的大量实验来证明我们的框架。
INTRODUCTION
简单的介绍了差分隐私最近几年的发展,和现在发展的方向,还介绍了本文和其之间的
Contributions
在本文中,我们考虑了受信任的数据分析师希望从包含许多个人用户个人数据的数据集中发布汇总统计数据的设置。每个用户都可能对其数据有不同的隐私要求,分析人员希望发布关于数据的有用的聚合信息,同时满足贡献者的个人隐私要求。为此,我们提出了一种新的隐私框架,称为个性化差异隐私(PDP),这是一种对差异隐私的推广,。我们还证明了差异隐私的组合属性可以遗传给PDP,允许从单个PDP组件构建复杂的隐私保护算法。
A.这可以利用非统一的隐私要求,以达到更好的效用,而不是通过差别的隐私。我们的第一种机制是通用的,可以很容易地将任何现有的差异私有算法自动转换为PDP算法。该机制是一个两步过程,涉5及到在单个元组级别上的非统一采样步骤,然后在采样数据集上调用适当的差异私有机制。在采样步骤中,根据相应用户的个人隐私需求计算每个元组的包含概率。我们证明,这两步程序引入的随机性的两个来源结合起来,产生了精确的个性化保证要求。我们的第二个机制是一种更直接的实现PDP的方法,。在第三节中,我们介绍了新的隐私定义,然后讨论了如何满足定义,在第四节中,第五节介绍了我们的实验研究,第六节总结了
B. 第二节:PRELIMINARIES
主要介绍差分隐私的概念
Definition 1 (Dataset).:
Definition 2 (Neighboring datasets):
Definition 3 (£-Differential Privacy):
Definition 4 (Global Sensitivity ).:
Theorem 1 (Laplace Mechanism ):
Theorem 2 (Exponential Mechanism)
[if !supportLists]C. [endif]Related Work
k-匿名的个性化隐私:要求一条数据至少和其他k-1条记录不可分,这通常是通过泛化或抑制属性值来实现的。在肖和陶的方法中,用户通过在泛化层次中为他们的数据指定最小泛化级别来指定他们的隐私偏好。(抑制:就是用一个没有意义的符号去代替某一个值,泛化:用不够具体但在语义上一致)
后面主要说和最近的一些论文对比,本文的陈述和技术贡献优越性,本文提供的算法:PDP的主要机制没有这样的限制;它可以自动将任何不同的私有算法——无论是拉普拉斯机制的实例、指数机制,还是多个不同私有模块的组合——转换成满足我们个性化隐私定义的算法,关于隐私拍卖的工作(在[2 1]中进行了调查),表面上与目前的工作相似。这项工作主要是关于如何准确计算用户群体的统计数据,这些用户要求对其参与所造成的隐私损失进行经济补偿。用户对其隐私进行(可能是非统一的)评估,表示参与e- difference私有分析(作为e的函数)所产生的隐私成本,以及如果使用其数据应支付的赔偿金额
Definition 5 (Privacy Specification):隐私规范是将: U -+ R+从用户映射到个人隐私好,其中较小的值表示较强的隐私偏好。Fleta"(0.01 , 1 .0)用来表示与用户对应的隐私偏好。
在实践中,期望典型用户选择有意义的数字隐私设置可能是不合理的。相反,我们设想这样一个场景:领域专家将适当的值与用户友好的描述符关联起来(例如,低、中、高隐私),用户从中进行选择。这是一种可能性;一般来说,为不同的私有系统选择一个合适的隐私参数是一个开放的问题,在本文中我们没有进一步考虑它。全局参数e,不能被个人影响,我们的模型假设隐私规范是公共知识。在传统的微分隐私这反映了情况,全球隐私设置€被假定为一个公共参数。但是,这意味着用户的隐私参数不能表示关于其敏感值的任何信息。我们认为这是一个合理的假设,因为隐私规范是在用户级别定义的,而不是在元组级别定义的。也就是说,我们可以将隐私设置看作是拥有数据的用户的函数,而不是数据的函数
Definition 6 (Personalized Differential Privacy (PDP)):
也就是将差分隐私里面的隐私预算换成了个人预算,从而保证个性化隐私
Theorem 3 (Differential Privacy Implies PDP):M : V -> R,满足£-DP也满足Fleta-PDP,with privacy specification = {(u,£) u 属于 U}.
Theorem 4 (Composition):证明过程大概就是讨论着证明连个过程串行时数据集在进行组合时候的处理,讨论两个算法有对数据集合中重复部分进行预算时候,为两个或多个算法隐私预算之和。若没有重合的话那么就是其中算法算法的隐私预算
原始机制:
我们现在引入的朴素基线机制在技术上实现了PDP,但是没有利用个性化的隐私偏来
福实用程序。在剩下的部分,我们将使用符号DP F€(D)来表示,计算输入在数据集D上的函
数f()并且满足满足传统€-DP微分隐私的任何计算机制。DP F€(D)可以是用来实现指
机制或者laplace机制或者更复杂的组合。最简单的就是直接应用应用原理3,我们找到
小的个人隐私用户预算,然后将其作为该函数的隐私预算,达到最强的隐私保护作用,以
下就是最小化的的隐私预算,(讲真,这种做法感觉绕圈子,从每个用户上升到了全体来阐释什么是差分隐私,不过这样写,也就是说,最小的,即这个就是最严格的,但这个超过了大多数人的需要,而且太强烈意味着要添加更多噪音,影响数据的使用)
Definition 7 (Minimum):
定义和证明都很清楚,就不多做解释了。
如果有一个数据集,里面较多的人不关注隐私,而一部分人关注隐私,一种做法就是对这个数据集进行分类,强的那一部分按照最严格的差分隐私方法执行
Definition 8 (Threshold):介绍了一个新的入门的机制
,也就是人为设置一个t,然后,用户对隐私要求在这之下的元组将会被删除,然后证明了这个满足差分隐私D6.
实现PDP通过抽样
我们现在为实现PDP提供了一种更智能的通用机制,在许多情况下,它能够获得比基线更高的实用级别。在计算中引入两个独立的随机性来源:1,元组级别的非均匀随机抽样,其中元组的包含概率取决于相应用户的个人隐私偏好.2:通过在抽样输入上调用传统的差异私有机制引入了额外的均匀随机性,其中隐私参数f依赖于t。将这两个随机性源组合在一起,就产生了每个元组所需的精确隐私量。(简单的说,就是先按个人隐私偏好进行随机抽样,然后对其进行个性化差分隐私处理。)
Definition 9 (The Sample Mechanism):表示独立随机的选择元组:
表示用户对元组x的隐私偏好,t是介于最大和最小的隐私偏好之间的们可以等于,入门的机制介绍完了,现在再来介绍简单机制,简单机制定义如下
R,romove随机选择删除
Theorem 5. The Sample mechanism Sf satisfies
-PDP
简单的机制满足
-PDP,以下是证明过程:备注:说受一片论文影响随机抽样有隐私放大的效果,这在第二章B部分有介绍
讨论:第一,可以把该机制看成黑盒子;第二:我们看到简单机制有效的引入两种随机机制的同时也引入了两种误差,t越小,抽样步骤丢弃的更少(抽样误差更低),但是会造成添加更多的噪音,t最小是就变成了最小线性机制,t最大的话就会变成给每个元组都提供了差分隐私保护,也就是很简单,较为基本的隐私保护
这个可调阈值t很有用,t是用户对自己数据集的隐私预算拼分,t很大时,提供完全E-DP机制的隐私保护,但有的人不需要,不一定达到最好的效果。通过较小的t,达到隐私预算,并且添加较小的噪音
由于抽样造成的误差不仅取决于隐私规范,而且还取决于数据的密度。因此,对于足够大的数据集,设置一个较低的阈值(例如,可以极大地提高具有强烈隐私要求的用户的样本率,代价是略微增加噪音,但总误差较低
下面有一个例子:
在总用户为200中,开始t=1,err=150,而将t=0.2.err=50。
实际上,采用改方法可以避免一种情况,全局敏感度很高,但对于大多数元组和集合度,敏感度较低,对输出的影响较小。
在实践中,为任意f精确地优化t可能不是件小事,因为尽管DP/可能在不了解数据集的情况下被量化,但抽样的影响确实取决于输入数据。因此,必须小心谨慎,以免通过调优过程泄露隐私。在某些情况下,一种可能的选择是使用不再敏感(或不那么敏感)的旧数据(来自类似的分布),在不违反隐私的情况下近似地优化阈值。在其他情况下,可以使用较保守用户的部分隐私预算,并从数据子集估算所需的数量。我们推迟对阈值优化策略的深入研究,以供今后工作参考。在第五节中,我们将演示对于许多函数,设置t = max
或t =1/|u|
”的简单启发法,通常会在真实数据和隐私问题上给出良好的结果。
两步机制,通过采样步骤实现PDP,然后是一个标准的差异私有机制,接下来将介绍一种高效直接的机制。
指数机制,这里介绍了打分函数理解:r在F(D)中出现的次数,如果没有的话就是负数,表示需要经过多少次改变才能达到这个要求,邻近数据集不同,那我们就需要对不同的进行区分,以最大化r。
通过修改指数机制的打分函数,构成新的指数机制
Definition 10 (PE Mechanism)
函数F:D->R,数据集:D,隐私规范Theorem 6. The PE mechanism satisfies -PDP:
证明过程在附录,没看懂,df()表示什么意义?以下是大概想的:
表示D和D’相差几个元组,大概据说当查询函数为预定参数r是中用户设置的最大隐私预算,带盖就是将打分函数换了以后,输出到r的概率,原来是用指数机制(使其输出o∈O 的概率正比于exp(E*q(D,r))/2 dq,则说M 是满足 ϵ-DP 的指数机制),现在改了打分函数,所以我们就需要重新证明:
接下来就是三个式列:
Count实例:理解:
后面两个中位数和最大数,差不多就是这个意思
D. [endif]EXPERIMENTAL STUDY实验研究
接下来,我们将PDP机制应用于两个常见的聚合函数,count和中值,以及更复杂的多元线性回归任务。虽然count和中值是相对简单的函数,但它们是构建更复杂算法]的重要基元。对于计数函数和中值函数,我们比较了简单机制和类似指数的PE机制。对于线性回归,我们使用抽样机制来转换由Zhang.[33]引入的一种最近的线性回归差分私有方法,生成了algo的PDP版本算法。
本实验要证明该算法提供可调度的隐私保证,通过原数据集(包含用户对自己数据聚设置的隐私预算,没有设置也可以用均值代替)和生成数据集之间均方根误差来调节阈值t。
为了为我们的实验生成隐私规范,我们将用户(记录)随机分为三组:保守派,代表高度关注隐私的用户;适中,代表中等关注的用户;自由主义者,代表那些不太关心用户的人。保守组和中度组的用户比例由参数fc和fM决定;自由派用户的比例是1.0 - (fe + fM)“在我们的实验中使用的默认值是fc = 0.54和fM = 0.37。保守组和中等组的用户的隐私偏好分别从[ce, CM]和[CM, CL]区间(舍入到最接近的百分位)均匀随机绘制
下面是实验当中的一些一些参数变化范围:
实验数据集大小
实验数据集大小
计数当中出现1的次数
自由用户隐私预算
中等用户隐私预算
保守用户隐私预算
中位数查询当中的标准差
中位数查询当中的均值
保守派的用户比列
中等组的用户比列
自由组的用户比列
我们上面介绍了四种机制:最小数机制,入门机制,简单机制,新指数机制然后按照上面写的用数据集进行赋闲,里面可以说Laplace机制和指数机制或者他们的组合机制