用多元线性回归预测某产品利润

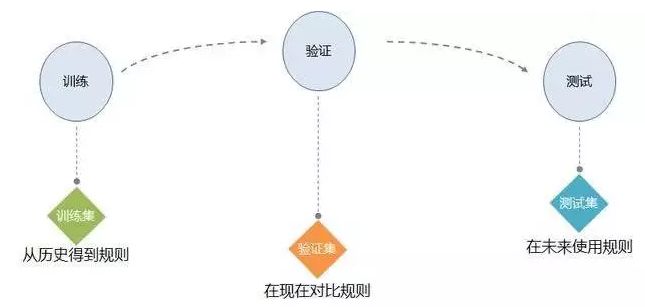
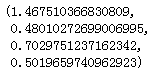数据挖掘流程

聚类分析是将数据对象，根据其特征自然分成不同类别。分类模型是针对已知类别，构建分类模型，探求未分类对象的类别。关联分析是通过数据对象之间的相关关系，发现对象之间的联系。预测估计就是根据已知连续数据对象，构建模型，对未知对象估值。

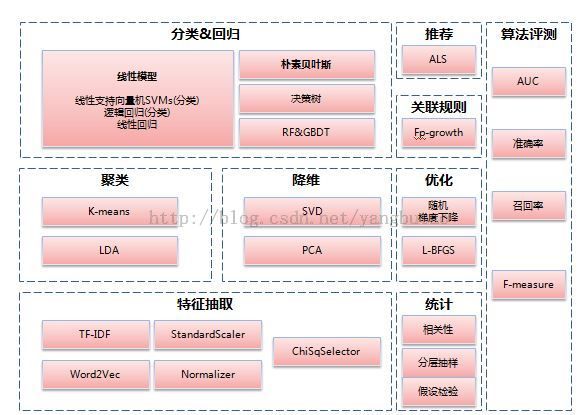
各类算法汇总

回归：根据已知变量预测某个连续的数值型变量

回归与分类的不同点在于，回归预测连续型变量，分类预测离散型变量。在回归方程中，求得最佳回归系数的方法是最小化误差的平方和。使用岭回归可以保证 X^T*X 的逆不能计算时，仍然能求得回归参数。

岭回归是缩减法的一种，相当于对回归系数的大小施加了限制。另一种很好的方法是 lasso 算法，难以求解，但可以使用简便的逐步线性回归来求得近似结果。

缩减法还可以看做对一个模型增加偏差（模型预测值与数据之间的差异）的同时减少方差（模型之间的差异）。

优点：结果易于理解，计算不复杂。

缺点：对非线性的数据拟合不好。

例如网站根据访问的历史数据预测用户的支付转化率

需导入专门用于统计建模的statsmodels模块中的ols函数

扩展：树回归

输入数据和目标变量之间呈现非线性关系，一种可行的方法是使用树对预测值分段，包括分段常数和分段直线。若叶节点使用的模型是分段常数则称为回归树，若叶节点使用的模型是分段直线则称为模型树。

CART 算法可以用于构造二元树并处理离散型或数值型数据的切分，该算法构造的回归树或模型树倾向于产生过拟合问题，可以采用预剪枝（在树的构建过程中就进行剪枝）和后剪枝（当树构建完毕再进行剪枝）。预剪枝更有效，但用户需要定义一些参数。

优点：可以对复杂的和非线性的数据建模。

缺点：结果不易理解。

一、一元线性回归

导入第三方模块
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
#导入数据集
income=pd.read_csv("F:\Salary_Data.csv")
income.head()

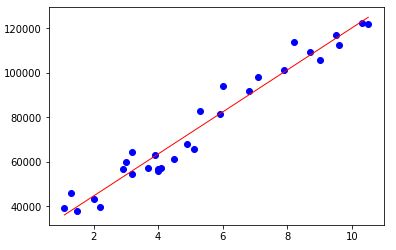
#绘制散点图
plt.scatter(x=income.YearsExperience,y=income.Salary,color="blue")
#导入统计建模模块
import statsmodels.api as sm
#构建一元线性回归模型
fit=sm.formula.ols("Salary~YearsExperience",data=income).fit()
#预测
pred=fit.predict(exog=income.YearsExperience)
#绘制回归线
plt.plot(income.YearsExperience,pred,color="red",linewidth=1)
plt.show()
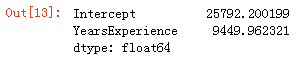
#返回模型的参数值
fit.params

ols函数中还有subset（获取子集）、drop_cols（删除变量）
predict函数中exog指定用于预测的自变量

即Salary=25792+9449YearsExperience

二、多元线性回归

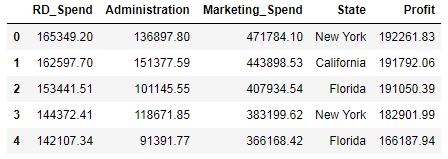
profit=pd.read_excel("F:\Predict to Profit.xlsx")
profit.head()

State为字符型的离散变量，需要处理为哑变量
为了建模和预测，将数据集拆分为80%训练集和20%测试集

# 导入模块
from sklearn import model_selection
# 生成由State变量衍生的哑变量
dummies = pd.get_dummies(profit.State)
# 将哑变量与原始数据集水平合并
profit_New = pd.concat([profit,dummies], axis = 1)
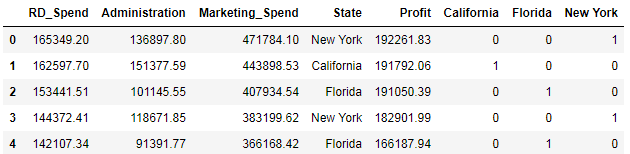
profit_New.head()

# 删除State变量和New York变量（因为State变量已被分解为哑变量，New York变量需要作为参照组）
profit_New.drop(labels = ['State','New York'], axis = 1, inplace = True)
profit_New.head()

从离散变量中衍生出来的哑变量只保留了Florida和Califorlia，而New York作为参照组

# 拆分数据集Profit_New
train, test = model_selection.train_test_split(profit_New, test_size = 0.2, random_state=1234)
# 建模
model2 = sm.formula.ols('Profit ~ RD_Spend + Administration + Marketing_Spend + Florida + California', data = train).fit()
print('模型的偏回归系数分别为：\n', model2.params)

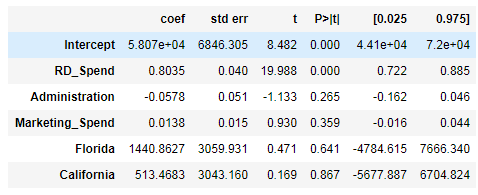
系数解释举例：
在其他变量不变的情况下，研发成本RD_Spend每增加1美元，利润增加0.8美元；
在其他变量不变的情况下，以New York为基准，如果在Florida销售产品，利润会增加1440.86美元

# 删除test数据集中的因变量Profit，用剩下的自变量进行预测
test_X = test.drop(labels = 'Profit', axis = 1)
pred = model2.predict(exog = test_X)
print('对比预测值和实际值的差异：\n',pd.DataFrame({'Prediction':pred,'Real':test.Profit}))

以上为测试集上的预测值

三、回归模型的假设检验

1.F检验

#模型的显著性检验--F检验
model2.fvalue

# 统计变量个数和观测个数
p = model2.df_model
n = train.shape[0]
p,n

需要对比F统计量的值与理论F分布的值，根据置信水平0.05和自由度（5,34）查看对应分布值

# 导入模块
from scipy.stats import f
# 计算F分布的理论值
F_Theroy = f.ppf(q=0.95, dfn = p,dfd = n-p-1)
print('F分布的理论值为：',F_Theroy)

174>2.5，则拒绝原假设，模型显著

2.t检验

#回归系数的显著性检验--t检验
# 模型的概览信息
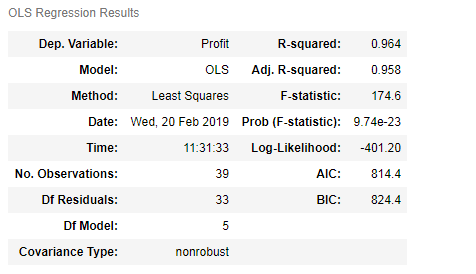
model2.summary()

从第二部分t对应的p值可以看出，截距项和研发成本p值<0.05，拒绝原假设，系数显著

第三部分主要涉及模型误差项的有关信息，DW用于检验误差项独立性，JB用于衡量误差项是否服从正态分布，以及误差项偏度Skew，峰度Kurtosis

四、回归模型的诊断

1.正态性检验

确保因变量服从正态分布

定性的图形法（直方图、PP、QQ）
定量的非参数法（Shapiro、K-S）

CASE1：直方图

# 直方图法
# 导入第三方模块
import scipy.stats as stats
# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 绘制直方图
sns.distplot(profit_New.Profit, bins = 10, fit = stats.norm, norm_hist = True,
             hist_kws = {'color':'steelblue', 'edgecolor':'black'}, 
             kde_kws = {'color':'black', 'linestyle':'--', 'label':'核密度曲线'}, 
             fit_kws = {'color':'red', 'linestyle':':', 'label':'正态密度曲线'})
# 显示图例
plt.legend()
# 显示图形
plt.show()

kde默认为TRUE，
fit需要指定一个随机分布对象（需要调用scipy模块中的随机分布函数），用于绘制随机分布的概率密度曲线，
norm_hist=True，表示将频数更改为频率，
plt.legend(）对应label

绘制了直方图、和密度曲线、理论正态分布的密度曲线，两条曲线近似吻合，直观上认为利润变量服从正态分布

CASE2：PP和QQ图

#导入统计建模模块
import statsmodels.api as sm
# 残差的正态性检验（PP图和QQ图法）
pp_qq_plot = sm.ProbPlot(profit_New.Profit)
# 绘制PP图
pp_qq_plot.ppplot(line = '45')
plt.title('P-P图')
# 绘制QQ图
pp_qq_plot.qqplot(line = 'q')
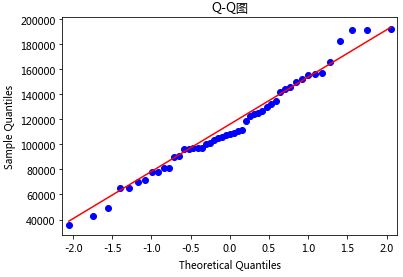
plt.title('Q-Q图')
# 显示图形
plt.show()

PP图的思想是比对正态分布的累计概率值和实际分布的累计概率值；
QQ图的思想是比对正态分布的分位数和实际分布的分位数

从结果可以看出，绘制的散点均落在直线的附近，没有较大的偏离，故认为利润变量近似服从正态分布

CASE3：Shapiro
原假设为变量服从正态分布，数据量低于5000，使用Shapiro，反之

通过scipy模块的子模块stats中的函数

# 导入模块
import scipy.stats as stats
stats.shapiro(profit_New.Profit)

第一个元素为Shapiro检验的统计量值，第二个是对应的概率值p，由于p>0.05,接受原假设，即服从正态分布

2.多重共线性检验

确保自变量之间不存在多重共线性

通过方差膨胀因子VIF值，>10，存在；>100，严重存在

# 导入statsmodels模块中的函数
from statsmodels.stats.outliers_influence import variance_inflation_factor
# 自变量X(包含RD_Spend、Marketing_Spend和常数列1)
X = sm.add_constant(profit_New.ix[:,['RD_Spend','Marketing_Spend']])

# 构造空的数据框，用于存储VIF值
vif = pd.DataFrame()
vif["features"] = X.columns
vif["VIF Factor"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
# 返回VIF值
vif

均低于10，不存在共线性，如果存在，考虑删除变量或者重新选择模型（岭回归或者Lasso）

3.线性相关性检验

确保用于建模的自变量和因变量之间存在线性关系

# 计算数据集Profit_New中每个自变量与因变量利润之间的相关系数
profit_New.drop('Profit', axis = 1).corrwith(profit_New.Profit)

<0.3几乎不相关；0.3-0.5弱相关；0.5-0.8中度相关；>0.8高度相关

管理成本与利润的相关系数只有0.2，不相关，只能说明不存在线性关系，有可能存在非线性关系，通过散点图矩阵

通过seaborn模块的pairplot函数

# 散点图矩阵
# 导入模块
import matplotlib.pyplot as plt
import seaborn as sns
# 绘制散点图矩阵
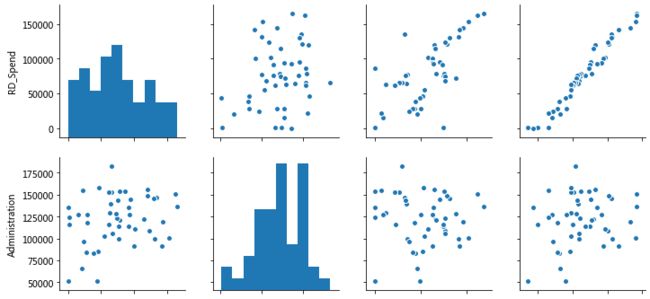
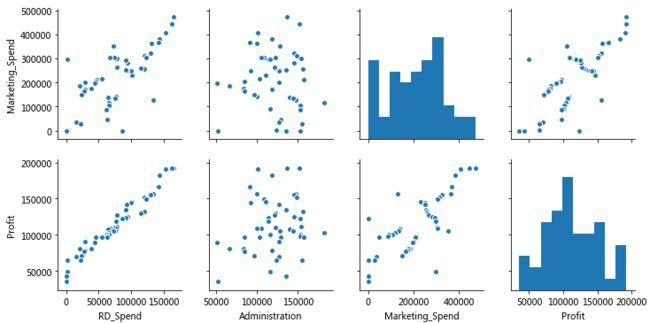
sns.pairplot(profit_New.ix[:,['RD_Spend','Administration','Marketing_Spend','Profit']])
# 显示图形
plt.show()

由于California与Florida都是哑变量，没有放入散点图矩阵

管理成本和利润呈水平趋势，而且分布比较宽，确实没有任何关系

综合考虑相关系数、散点图矩阵、t检验，最后只保留RD_Spend和Marketing-Spend两个自变量

# 模型修正
model3 = sm.formula.ols('Profit ~ RD_Spend + Marketing_Spend', data = train).fit()
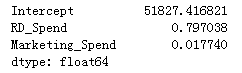
# 模型回归系数的估计值
model3.params

4.异常值检验

已经建立了一个回归模型，并且基于get_influence方法获得四种检查异常值的方法

# 异常值检验
outliers = model3.get_influence()

# 高杠杆值点（帽子矩阵）
leverage = outliers.hat_matrix_diag
# dffits值
dffits = outliers.dffits[0]
# 学生化残差
resid_stu = outliers.resid_studentized_external
# cook距离
cook = outliers.cooks_distance[0]

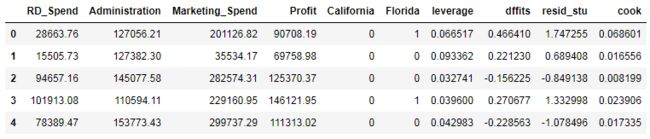
# 合并各种异常值检验的统计量值
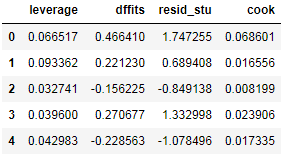
contat1 = pd.concat([pd.Series(leverage, name = 'leverage'),pd.Series(dffits, name = 'dffits'),
                     pd.Series(resid_stu,name = 'resid_stu'),pd.Series(cook, name = 'cook')],axis = 1)
contat1.head()

# 重设train数据的行索引
train.index = range(train.shape[0])
train.index

# 将上面的统计量与train数据集合并
profit_outliers = pd.concat([train,contat1], axis = 1)
profit_outliers.head()

选择其中一种，例如标准化残差，当大于2时，认为是异常点

# 计算异常值数量的比例
outliers_ratio = sum(np.where((np.abs(profit_outliers.resid_stu)>2),1,0))/profit_outliers.shape[0]
outliers_ratio

如果异常样本比例小于等于5%,可以将异常点删除；
如果比例较高，需要对于异常点，设置哑变量的值为1，否则为9

异常比例为2.5%，此时删除，再重新构建模型

# 挑选出非异常的观测点
none_outliers = profit_outliers.ix[np.abs(profit_outliers.resid_stu)<=2,]

# 应用无异常值的数据集重新建模
model4 = sm.formula.ols('Profit ~ RD_Spend + Marketing_Spend', data = none_outliers).fit()
model4.params

5.独立性检验

残差的独立性检验即因变量y的独立性检验，DW在2左右，残差项不相关，与2偏差的较远，残差不独立

# Durbin-Watson统计量
# 模型概览
model4.summary()

残差独立

6.方差齐性检验

模型残差项的方差不随自变量的变动而呈现某种趋势，即方差为1个常数

通过图形法（散点图）和BP检验

CASE1：残差与自变量之间的散点图

# 方差齐性检验
# 设置第一张子图的位置
ax1 = plt.subplot2grid(shape = (2,1), loc = (0,0))
# 绘制散点图
ax1.scatter(none_outliers.RD_Spend, (model4.resid-model4.resid.mean())/model4.resid.std())
# 添加水平参考线
ax1.hlines(y = 0 ,xmin = none_outliers.RD_Spend.min(),xmax = none_outliers.RD_Spend.max(), color = 'red', linestyles = '--')
# 添加x轴和y轴标签
ax1.set_xlabel('RD_Spend')
ax1.set_ylabel('Std_Residual')

# 设置第二张子图的位置
ax2 = plt.subplot2grid(shape = (2,1), loc = (1,0))
# 绘制散点图
ax2.scatter(none_outliers.Marketing_Spend, (model4.resid-model4.resid.mean())/model4.resid.std())
# 添加水平参考线
ax2.hlines(y = 0 ,xmin = none_outliers.Marketing_Spend.min(),xmax = none_outliers.Marketing_Spend.max(), color = 'red', linestyles = '--')
# 添加x轴和y轴标签
ax2.set_xlabel('Marketing_Spend')
ax2.set_ylabel('Std_Residual')

# 调整子图之间的水平间距和高度间距
plt.subplots_adjust(hspace=0.6, wspace=0.3)
# 显示图形
plt.show()

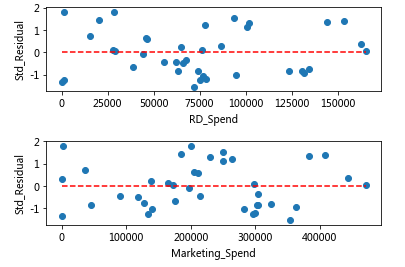
标准化残差没有随自变量的变动而呈现喇叭形，所有散点几乎均匀分布在参考线y=0附近，方差齐性

CASE2：BP检验
原假设是残差的方差为1个常数

# BP检验
sm.stats.diagnostic.het_breushpagan(model4.resid, exog_het = model4.model.exog)

第二个值为p值>0.05，接受原假设，方差齐性

五、回归模型的预测

# 模型预测
# model4对测试集的预测
pred4 = model4.predict(exog = test.ix[:,['RD_Spend','Marketing_Spend']])
# 对比预测值与实际值
pd.DataFrame({'Prediction':pred4,'Real':test.Profit})

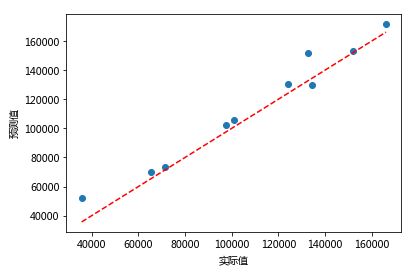
# 绘制预测值与实际值的散点图
plt.scatter(x = test.Profit, y = pred4)
# 添加斜率为1，截距项为0的参考线
plt.plot([test.Profit.min(),test.Profit.max()],[test.Profit.min(),test.Profit.max()],
        color = 'red', linestyle = '--')
# 添加轴标签
plt.xlabel('实际值')
plt.ylabel('预测值')
# 显示图形
plt.show()

如果预测值和实际值非常接近，那么得到的散点图在对角线附近微微波动，从图中可看出，预测效果还不错。