树
记录《剑指offer》中所有关于树的题目,以及LeetCode中的相似题目。
相关题目列表
| index | description | key words | done | data |
|---|---|---|---|---|
| 6 | 重建二叉树 | 遍历,重建 | Y | 18-3-7 |
| 18 | 树的子结构 | 遍历,递归 | Y | 18-3-7 |
| 19 | 二叉树的镜像 | 遍历,镜像 | Y | 18-3-8 |
| 23 | 从上往下打印二叉树 | 层序遍历 | Y | 18-3-8 |
| 24 | 二叉搜索树的后序遍历序列 | BST | Y | 18-3-9 |
| 25 | 二叉树中和为某一值的路径 | 路径和 | Y | 18-3-9 |
| 27 | 二叉搜索树与双向链表 | BST与链表 | Y | 18-3-12 |
| 39_1 | 二叉树的深度 | 树的深度 | Y | 18-3-12 |
| 39_2 | 判断是否是AVL树 | 深度,AVL树 | Y | 18-3-13 |
| 50 | 树中两个结点的最低公共祖先 | 公共祖先 | Y | 18-3-13 |
| 58 | 二叉树的下一个结点 | 下一结点 | Y | 18-3-15 |
| 59 | 对称的二叉树 | 遍历,对称 | Y | 18-3-15 |
| 60 | 把二叉树打印成多行 | 层序遍历 | Y | 18-3-17 |
| 61 | 按之字顺序打印二叉树 | 层序遍历 | Y | 18-3-17 |
| 62 | 序列化二叉树 | 序列化 | Y | 18-3-18 |
| 63 | 二叉搜索树的第k个结点 | BST,中序遍历 | Y | 18-3-18 |
题目
树是一种最常考的数据结构,尤其是二叉树,其中二叉树的各种遍历方法,以及树的各种子结构操作,都需要灵活掌握。
面试题6: 重建二叉树
题目: 输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不包含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建出如下图的二叉树,并输出它的头结点。
题目分析
根据二叉树的前序遍历与中序遍历序列的特定,可以判断节点直接的相对位置,从而得出重构二叉树。
具体的做法是,根据前序遍历得知根结点,然后根据中序遍历将序列分成左右子树,从而递归完成二叉树的重构。
参考代码
#include
#include
using namespace std;
struct BinaryTreeNode
{
int val;
BinaryTreeNode* left;
BinaryTreeNode* right;
BinaryTreeNode(int x) : val(x), left(NULL), right(NULL) {}
//输出前序遍历结果
static void PreOrder(BinaryTreeNode* root)
{
if (root == NULL)
{
return;
}
cout << root->val << " ";
PreOrder(root->left);
PreOrder(root->right);
}
//输出中序遍历结果,采用static
static void InOrder(BinaryTreeNode* root)
{
if (root == NULL)
{
return;
}
InOrder(root->left);
cout << root->val << " ";
InOrder(root->right);
}
//输出后序遍历结果
static void LatOrder(BinaryTreeNode* root)
{
if (root == NULL)
{
return;
}
LatOrder(root->left);
LatOrder(root->right);
cout << root->val << " ";
}
};
class Solution
{
public:
BinaryTreeNode* reConstructBinaryTree(vector pre, vector in)
{
//前序遍历的长度和中序遍历相同
if (pre.size() != in.size())
{
return NULL;
}
//长度不能为0
int length = pre.size();
if (length == 0)
{
return NULL;
}
//int length = pre.size();
int value = pre[0]; //前序遍历的第一个结点是根结点
BinaryTreeNode *root = new BinaryTreeNode(value);
//找到中序遍历中的根结点
int rootIndex = 0;
for (int i = 0; i < length; ++i)
{
if (in[i] == value)
{
rootIndex = i;
break;
}
}
//区分左子树和右子树
//中序遍历中,根左边的就是左子树,右边的就是右子树
//前序遍历中,根后面的是先遍历左子树,然后遍历右子树
//首先确定左右子数的长度,从中序遍历in中确定
vector preLeft, inLeft, preRight, inRight;
for (int i = 0; i < rootIndex; ++i)
{
//前序遍历的第一个结点是根结点,所以是i+1
preLeft.push_back(pre[i+1]);
//中序遍历的前i个结点即使中序遍历的左子树
inLeft.push_back(in[i]);
}
for (int i = rootIndex + 1; i < length; ++i)
{
//前序遍历的右子树
preRight.push_back(pre[i]);
//中序遍历的右子树
inRight.push_back(in[i]);
}
root->left = reConstructBinaryTree(preLeft, inLeft);
root->right = reConstructBinaryTree(preRight, inRight);
return root;
}
};
int main()
{
int pre[] = {1,2,4,7,3,5,6,8};
int in[] = {4,7,2,1,5,3,8,6};
vector preOrder(pre, pre+8);
vector inOrder(in, in+8);
Solution solu;
BinaryTreeNode *root = solu.reConstructBinaryTree(preOrder, inOrder);
cout << root->val << endl;
BinaryTreeNode::PreOrder(root);
cout << endl;
BinaryTreeNode::InOrder(root);
cout << endl;
BinaryTreeNode::LatOrder(root);
return 0;
}
相似题目
本题与LeetCode中的105. Construct Binary Tree from Preorder and Inorder Traversal
完全一致,另外LeetCode中还有一道已知中序和后续的题目106. Construct Binary Tree from Inorder and Postorder Traversal
,这两题的参考代码见:
LeetCode 105 code
LeetCode 106 code
还可以在牛客网 剑指offer上完成对本题的练习。
面试题18:树的子结构
题目: 输入两棵二叉树A和B,判断B是不是A的子结构。
题目分析
要查找A中是否存在和B结构一样的子树,可以分为两步进行:第一步在A中找到和B的根结点的值一样的结点R,第二步判断树A中以R为根结点的子树是不是包含和树B一样的结构。
第一步在树A中查找结点,这实际上就是树的遍历,遍历可以采用递归的方式完成。
第二步是判断A中以R为根结点的子树是不是和B有相同的结构,也可以采用递归的方式完成。
参考代码
#include
using namespace std;
struct BinaryTreeNode
{
int val;
BinaryTreeNode* left;
BinaryTreeNode* right;
};
class Solution
{
public:
//寻找到与tree2根结点相同的结点。才执行之后的操作,若是找不到则向下遍历,知道找到再判断左右子树。
bool HasSubtree(BinaryTreeNode* pRoot1, BinaryTreeNode* pRoot2)
{
bool result = false;
if (pRoots != NULL && pRoot2 != NULL) //两棵树不能为空
{
if (pRoot1->val == pRoot2->val) //根结点相等之后,转为比较左右子结点
result = DoesTreeHaveTree2(pRoot1, pRoot2);
if (!result) //左右子节点不满足条件,在tree1中重新寻找与tree2根结点相等的结点
result = HasSubtree(pRoot1->left, pRoot2); //在左子树中找
if (!result)
result = HasSubtree(pRoot1->right, pRoot2); //在右子树中找
}
return result;
}
private:
bool DoesTreeHaveTree2(BinaryTreeNode* pRoot1, BinaryTreeNode* pRoot2)
{
if (pRoot2 == NULL) //经过查找对比,最好到了tree2的叶子节点,则遍历结束。返回true,这个条件必须在下一个条件之前
return true;
if (pRoot1 = NULL) //若查找对比最后到了tree1的叶子节点则,证明没有找到对应的子树
return false;
if (pRoot1->val != pRoot2->val)
return false;
//如果根结点相等,则分别判断左右子树
return DoesTreeHaveTree2(pRoot1->left, pRoot2->left) && DoesTreeHaveTree2(pRoot1->right, pRoot2->right);
}
};
相似题目
本题与LeetCode中的572. Subtree of Another Tree完全一致,参考代码见:
LeetCode 572 code
还可以在牛客网 剑指offer上完成对本题的练习。
面试题19: 二叉树的镜像
题目: 请完成一个函数,输入一个二叉树,该函数输出它的镜像。
题目分析
分析题目可知,二叉树的镜像问题,其实就是递归交换根结点的左右子树的问题。
于是,我们通过先序遍历这棵树的每个结点,如果该结点存在你左右子树,就交换它的两个子结点,当交换玩所有非叶子节点的左右子结点后,就得到了二叉树的镜像。
参考代码
#include
using namespace std;
struct BinaryTreeNode
{
int val;
BinaryTreeNode* left;
BinaryTreeNode* right;
BinaryTreeNode(int x): val(x), left(NULL), right(NULL) {}
static void PreOrder(BinaryTreeNode* root)
{
if (root == NULL)
return;
cout << root->val << " ";
PreOrder(root->left);
PreOrder(root->right);
}
static void InOrder(BinaryTreeNode* root)
{
if (root == NULL)
return;
InOrder(root->left);
cout << root->val << " ";
InOrder(root->right);
}
static void LatOrder(BinaryTreeNode* root)
{
if (root == NULL)
return;
LatOrder(root->left);
cout << root->val << " ";
LatOrder(root->right);
}
};
class Solution
{
public:
void mirrorOfBinaryTree(BinaryTreeNode* pNode)
{
if (pNode == NULL)
return NULL;
if (pNode->left == NULL && pNode->right == NULL) //µÝ¹é½áÊøÌõ¼þ
return NULL;
BinaryTreeNode* temp;
temp = pNode->left;
pNode->left = pNode->right;
pNode->right = temp;
if (pNode->left)
mirrorOfBinaryTree(pNode->left);
if (pNode->right)
mirrorOfBinaryTree(pNode->right);
}
};
相似题目
本题与LeetCode中的226. Invert Binary Tree一题完全一致,参考代码见:
LeetCode 226 code
还可以在牛客网 剑指offer上完成对本题的练习。
面试题23: 从上往下打印二叉树
题目: 从上往下打印二叉树的每个结点,同一层的结点按照从左往右的顺序打印。
题目分析
本题是二叉树的层序遍历,使用双向队列完成。
参考代码
//二叉树的层序遍历
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
vector PrintFromTopToBottom(TreeNode* root) {
vector result;
if (root == NULL)
return result;
std::deque dequeTreeNode; //利用队列先入先出的特性
dequeTreeNode.push_back(root);
while (dequeTreeNode.size()){ //如果队列中存在元素,在弹出首元素的同时压入这个元素对应的左右子树
TreeNode* pNode = dequeTreeNode.front();
result.push_back(pNode->val);
dequeTreeNode.pop_front();
if (pNode->left != NULL)
dequeTreeNode.push_back(pNode->left);
if (pNode->right != NULL)
dequeTreeNode.push_back(pNode->right);
}
return result;
}
};
相似题目
本题与LeetCode中的102. Binary Tree Level Order Traversal
完全一致,另外LeetCode中还有一道本题的延伸107. Binary Tree Level Order Traversal II
。这两题的参考代码见:
LeetCode 102 code
LeetCode 107 code
还可以在牛客网 剑指offer上完成对本题的练习。
面试题24: 二叉搜索树的后续遍历序列
题目: 输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是返回true,否则返回false。假设输入的数组的任意两个数字都互不相同。
题目分析
首先,二叉搜索树要求每个结点左子树的值都小于本结点的值,所有右子树上的值都大于本节点的值。
以数组{5,7,6,9,11,10,8}为例,后序遍历中8为树的根结点,所以5,7,6为8的左子树,9,11,10为8的右子树,因此在8结点上满足条件。由此可以用相同的方法判断每个非叶子结点是否都满足二叉搜索树的条件。
参考代码
class Solution {
public:
bool VerifySquenceOfBST(vector sequence) {
int length = sequence.size();
if (length == 0)
return false;
return result(sequence, 0, length - 1);
}
private:
bool result(vector sequence, int start, int end){
if (start >= end)
return true; //递归结束条件
int root = sequence[end];
int i = start;
while (sequence[i] < root){
++i;
}
//判断右子树
int j = i;
while (j < end){
if (sequence[j] < root){
return false;
}
++j;
}
return result(sequence, start, i-1) && result(sequence, i, end-1);
}
};
相似题目
LeetCode中有一道是验证二叉搜索树的前序序列,但是是一道收费题255
Verify Preorder Sequence in Binary Search Tree ,其实方法都是一样的。
可以在牛客网 剑指offer上对本题进行练习。
面试题25: 二叉树中和为某一值的路径
题目: 输入一棵二叉树和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
题目分析
此题用前序遍历的方式访问到某一结点时,我们把该结点添加到路径上,并累加该结点的值。如果该结点为叶结点并且路径中结点值的和正好等于输入整数,则当前路径符合,打印出来。如果当前结点不是叶结点,则继续访问它的子结点。当前结点结束访问后,递归函数将自动回到它的父结点。因此我们在函数退出之前要在路径上删除当前结点并减去当前结点的值,以确保返回父结点时路径刚好是从根结点到父结点的路径。我们不难看出,这其实就是一个栈,因为路径要与递归调用状态一致,而递归调用的本质就是一个压栈和出栈的过程。
参考代码
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
vector> res; //将res和path设置为全局变量
vector path;
vector> FindPath(TreeNode* root,int expectNumber) {
find(root, expectNumber);
return res;
}
private:
void find(TreeNode* root, int sum){
if (root == NULL)
return;
path.push_back(root->val);
bool isLeaf = root->left == NULL && root->right == NULL;
if ((root->val == sum) && isLeaf){ //判断是否满足条件
res.push_back(path);
}
else{ //如果不满足,则递归
if (root->left != NULL)
find(root->left, sum - root->val);
if (root->right != NULL)
find(root->right, sum - root->val);
}
path.pop_back(); //在返回到父结点之前,在路径上删除当前节点
}
};
相似题目
本题与LeetCode中的113. Path Sum II完全一致,另外LeetCode中还有两道类似题目,分别是本题的简化版本(判断是否存在一个路径)112. Path Sum; 以及强化版本(不设定路径起始限制)437. Path Sum III
这三道题的参考代码见:
LeetCode 113 code
LeetCode 112 code
LeetCode 437 code
还可以在牛客网 剑指offer上完成对本题的练习。
面试题27: 二叉树与双向链表
题目: 输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
题目分析
根据BST与排序双向链表的关系,原先指向左子结点的指针调整为链表中指向前一个结点的指针,原先指向右子结点的指针调整为链表中指向后一个结点的指针。
接下来我们考虑如何进行转换。
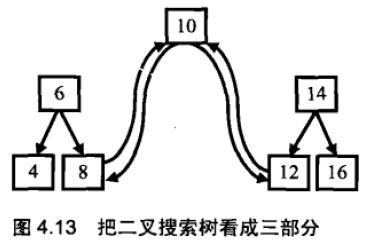
根据BST中序遍历有序的特点,我们采用中序遍历算法从小到大遍历二叉树的每一个结点。当遍历到根结点时,我们把树看成3部分(如下图所示),值为10的结点、根结点值为6的左子树,根结点值为14的右子树。根据排序链表的定义,值为10的节点将和它的左子树的最大一个节点相连,同时与右子树中最小节点相连。
根据中序遍历的顺序,当我们遍历转换到根结点时,它的左子树已经转换成一个排序链表了,并且最后一个节点即为其中最大的结点。我们把8与10相连即可。接着遍历转换右子树,并把根结点和右子树中最小的结点相连。
参考代码
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
TreeNode* Convert(TreeNode* pRootOfTree)
{
TreeNode* pLastNodeInList = NULL;
ConverNode(pRootOfTree, &pLastNodeInList); //因为函数形参是二重指针,所以需要用取地址符
TreeNode* pHeadOfList = pLastNodeInList;
while (pHeadOfList != NULL && pHeadOfList->left != NULL)
pHeadOfList = pHeadOfList->left;
return pHeadOfList;
}
private:
//类似于中序遍历
void ConverNode(TreeNode* pNode, TreeNode** pLastNodeInList){ //因为需要对pLastNodeInList进行动态改变,所以需要用二重指针
if (pNode == NULL)
return;
TreeNode* pCurrent = pNode;
if (pCurrent->left != NULL)
ConverNode(pCurrent->left, pLastNodeInList);
pCurrent->left = *pLastNodeInList;
if (*pLastNodeInList != NULL)
(*pLastNodeInList)->right = pCurrent;
*pLastNodeInList = pCurrent;
if (pCurrent->right != NULL)
ConverNode(pCurrent->right, pLastNodeInList);
}
};
相似题目
本题与LeetCode中的109. Convert Sorted List to Binary Search Tree类似,其是将单链表转化为BST。
还可以在牛客网 剑指offer上完成对本题的练习。
面试题39_1: 二叉树的深度
题目: 输入一棵二叉树的根结点,求该树的深度。从根结点到叶结点一次经过的节点形成树的一条路径,最长路径的长度为树的深度。
题目分析
首先我们可以采用面试题25中的方法寻找路径,即可得到深度。
这里我们采用一种新的方法。
如果一棵二叉树只有一个根结点,则它的深度为1,如果只有右子树而没有左子树,则其深度就是1+右子树的深度,以此类推,从而形成一个递归。
参考代码
#include
using namespace std;
struct TreeNode
{
int val;
TreeNode* left;
TreeNode* right;
};
class Solution
{
public:
int TreeDepth(TreeNode* pRoot)
{
if (pRoot == NULL)
return 0;
int Left = TreeDepth(pRoot->left);
int Right = TreeDepth(pRoot->right);
return 1+(Left >= Right) ? Left : Right;
}
};
相似题目
本题与LeetCode中的104. Maximum Depth of Binary Tree与111. Minimum Depth of Binary Tree类似,其分别是求二叉树的最大最小深度。参考代码见:
LeetCode 104 code
LeetCode 111 code
还可以在牛客网 剑指offer上完成对本题的练习。
题目39_2: 判断是否为AVL树
题目: 输入一棵二叉树的根结点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
题目分析
可以根据39_1中二叉树的深度逐结点判断左右子树深度差,从而确定是否是AVL树,但是这样做的缺点是显而易见的,每个节点需要访问多次。
下面采用一种新的方法:
如果我们采用后序遍历的方式遍历二叉树的每一个结点,在遍历到一个结点之前,我们就已经遍历了它的左右子树。只要在遍历每个结点的时候记录它的深度,我们就可以一边遍历一边判断每个节点是不是平衡的。
参考代码
struct TreeNode
{
int val;
TreeNode* left;
TreeNode* right;
};
/*===============方法一,需要多次遍历同一节点====================*/
class Solution
{
public:
bool IsBalancedTree(TreeNode* pRoot)
{
if (pRoot == NULL)
return true;
int Left = TreeDepth(pRoot->left);
int Right = TreeDepth(pRoot->right);
int diff = Left - Right;
if (diff > 1 || diff < -1)
return false;
return IsBalancedTree(pRoot->left) && IsBalancedTree(pRoot->right);
}
private:
int TreeDepth(TreeNode* pRoot)
{
if (pRoot == NULL)
return 0;
int Left = TreeDepth(pRoot->left);
int Right = TreeDepth(pRoot->right);
return (Left >= Right) ? (Left + 1) : (Right + 1); //更新深度
}
};
/*====================方法二,每个节点只需要遍历一次======================*/
class Solution2
{
public:
bool IsBalancedTree(TreeNode* pRoot)
{
int Depth = 0;
return IsBalanced(pRoot, Depth);
}
private:
bool IsBalanced(TreeNode* pRoot, int& depth) //必须将depth设置为引用,因为在遍历过程中depth需要改变
{
if (pRoot == NULL) //递归结束条件
{
depth = 0;
return true;
}
int left = right = 0;
if (IsBalanced(pRoot->left, left) && IsBalanced(pRoot->right, right))
{
int diff = left - right;
if (diff <= 1 && diff >= -1)
{
depth = 1 + (left>right?left:right); //更新depth
return true;
}
}
return false;
}
};
相似题目
本题与LeetCode中的110. Balanced Binary Tree
完全一致。参考代码见:
LeetCode 110 code
还可以在牛客网 剑指offer上完成对本题的练习。
面试题50: 树中两个结点的最低公共祖先
题目: 首先如果树是二叉树,或者是BST这就是不同的题目,首先如果是BST,那由于BST的排序性,只需要将这两个结点与根结点对比,判断两个节点是在左右子树中,如果这两个节点分别在左右子树中,则根结点即为所求。依次类推,只需要从上到下找到这两个结点之间的第一个结点即为所求。
如果是一棵普通二叉树,本题最好的做法是通过两个辅助链表记录到两个结点的路径,从而将其转化为求两个链表的最后公共结点。
参考代码
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
//TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == NULL || p == NULL || q == NULL)
return NULL;
list path1;
list path2;
GetNodePath(root, p, path1); //待会判断真假
GetNodePath(root, q, path2);
return GetLastCommonNode(path1, path2);
}
private:
bool GetNodePath(TreeNode* root, TreeNode* pNode, list &path){ //得到节点路径
path.push_back(root);
if (root == pNode)
return true;
bool found = false;
if (!found && root->left != NULL)
found = GetNodePath(root->left, pNode, path);
if (!found && root->right != NULL)
found = GetNodePath(root->right, pNode, path);
if (!found)
path.pop_back();
return found;
}
TreeNode* GetLastCommonNode(list path1, list path2){ //寻找两跳路径上的最后一个公共节点
list::iterator iterator1 = path1.begin();
list::iterator iterator2 = path2.begin();
TreeNode* pLast = NULL;
while (iterator1 != path1.end() && iterator2 != path2.end()){
if (*iterator1 == *iterator2)
pLast = *iterator1;
iterator1++;
iterator2++;
}
return pLast;
}
};
相似题目
LeetCode中235. Lowest Common Ancestor of a Binary Search Tree
一题为找到BST两个结点的最低公共结点,236. Lowest Common Ancestor of a Binary Tree
为二叉树寻找公共结点。这两题的参考代码见:
LeetCode 235 code
LeetCode 236 code
面试题58: 二叉树的下一个结点
题目: 给定一个二叉树和其中一个结点,如何找出中序遍历顺序的下一个结点?树中的结点除了有两个分别指向左右子结点的指针以外,还有一个指向父结点的指针。
题目分析
根据二叉树的结构,本题中所给节点有如下几种情况:
1、如果一个节点有右子树,则其下一个结点就是它右子树中最左子结点。
2、如果没有右子树:
2.1 如果结点就是它父结点的左子结点,则它的下一个结点就是它的父结点。
2.2 如果一个节点既没有右子树,并且还是它父结点的右子结点,这种情形比较复杂。我们可以沿着指向父结点的指针一直向上遍历,直到找到一个是它父结点的左子结点的节点,这个结点如果存在,则它的父结点就是我们要找的下一个结点。
参考代码
/*
struct TreeLinkNode {
int val;
struct TreeLinkNode *left;
struct TreeLinkNode *right;
struct TreeLinkNode *next;
TreeLinkNode(int x) :val(x), left(NULL), right(NULL), next(NULL) {
}
};
*/
class Solution {
public:
TreeLinkNode* GetNext(TreeLinkNode* pNode)
{
if (pNode == NULL)
return NULL;
TreeLinkNode* pRes = NULL;
if (pNode->right != NULL){
TreeLinkNode* pRight = pNode->right;
while (pRight->left != NULL)
pRight = pRight->left;
pRes = pRight;
}
else{
while (pNode->next != NULL){ //直到找到此结点是其父结点的左孩子,如果是左子树,则直接返回,如果不是则向上找
if (pNode->next->left == pNode)
return pNode->next;
pNode = pNode->next;
}
pRes = pNode->next;
}
return pRes;
}
};
相似题目
可以在牛客网 剑指offer上完成对本题的练习。
面试题59: 对称的二叉树
题目: 请实现一个函数,用来判断一棵二叉树是不是对称的。
题目分析
可以通过这个二叉树的前序遍历与对称前序遍历是否相同来判断是否是对称二叉树。
参考代码
struct TreeNode
{
int val;
struct TreeNode* right;
struct TreeNode* left;
};
class Solution
{
public:
bool isSymmetrical(TreeNode* pRoot)
{
return isSymmetrical(pRoot, pRoot);
}
private:
bool isSymmetrical(TreeNode* pRoot1, TreeNode* pRoot2)
{
if (pRoot1 == NULL && pRoot2 == NULL) //两个同时为NULL
return true;
if (pRoot1 == NULL || pRoot2 == NULL) //如果只有一个先到达NULL
return false;
if (pRoot1->val != pRoot2->val) //一旦不相等
return false;
return isSymmetrical(pRoot1->left, pRoot2->right) && isSymmetrical(pRoot1->right, pRoot2->left);
}
};
相似题目
本题与LeetCode中的101. Symmetric Tree完全一致,参考代码见:
LeetCode 101 code
还可以在牛客网 剑指offer上完成对本题的练习。
面试题60:把二叉树打印成多行
题目: 从上到下按层打印二叉树,同一层的结点按从左到右的顺序打印,每一层打印到一行。
题目分析
本题与23题层序打印类似,可以使用双向队列来保存将要打印的结点。
参考代码
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
class Solution {
public:
vector> res;
vector > Print(TreeNode* pRoot) {
if (pRoot == NULL)
return res;
std::queue nodes;
nodes.push(pRoot);
while (!nodes.empty()){
vector temp;
int size = nodes.size();
for (int i = 0; i < size; ++i){
TreeNode* pNode = nodes.front();
temp.push_back(pNode->val);
nodes.pop();
if (pNode->left != NULL) nodes.push(pNode->left);
if (pNode->right != NULL) nodes.push(pNode->right);
}
res.push_back(temp);
}
return res;
}
};
相似题目
可以在牛客网 剑指offer上完成对本题的练习。
面试题61: 按之字形顺序打印二叉树
题目: 请实现一个函数,按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。
题目分析
本题与上一题一样都是二叉树的层序遍历的变型题,本题与传统层序遍历的区别在于,只需要维护一个变量,这个变量的作用是判断本行是从左往右还是从右向左。
参考代码
struct TreeNode
{
int val;
TreeNode* left;
TreeNode* right;
};
class Solution
{
public:
vector> res;
vector> Print(TreeNode* pRoot)
{
if (pRoot == NULL)
return res;
std::queue nodes;
nodes.push(pRoot);
bool even = false; //判断奇偶层,看是否需要reverse
while (!nodes.empty())
{
vector temp;
int size = nodes.size();
for (int i = 0; i < size; ++i)
{
TreeNode* pNode = nodes.front();
temp.push_back(pNode->val);
nodes.pop();
if (pNode->left != NULL) nodes.push(pNode->left);
if (pNode->right != NULL) nodes.push(pNode->right);
}
if (even)
std::reverse(temp.begin(), temp.end());
even = !even;
res.push_back(temp);
}
return res;
}
};
相似题目
本题与LeetCode中103. Binary Tree Zigzag Level Order Traversal完全一致,参考代码见:
LeetCode 103 code
还可以在牛客网 剑指offer上完成对本题的练习。
面试题62: 序列化二叉树
题目: 请事先两个函数,分别用来序列化和反序列化二叉树。
题目分析
本题采用流的方式完成对二叉树的序列化与反序列化。
参考代码
void Serialize(treeNode* root, ostream& stream) {
if (root == nullptr) {
stream << "#,";
return;
}
stream << "root->val" << ",";
Serialize(root->left, stream);
Serialize(root->right, stream);
}
void Deserialize(treeNode** root, istream& stream) {
int number;
if (ReadStream(stream, &number)) {
*root = new treeNode();
(*root)->val = number;
(*root)->left = nullptr;
(*root)->right = nullptr;
Deserialize( &((*root)->left), stream);
Deserialize( &((*root)->right), stream);
}
}
相似题目
可以在牛客网 剑指offer上完成对本题的练习。
面试题63: 二叉搜索树的第k个结点
题目: 给定一棵二叉搜索树,请找出其中的第k大的节点。
题目分析
如果以中序遍历的方式遍历一棵BST,则中序遍历的顺序就是递增的,于是我们只需要用中序遍历算法遍历一棵BST,就很容易找出它的第k大的结点。
参考代码
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
class Solution {
public:
TreeNode* KthNode(TreeNode* pRoot, int k)
{
if (pRoot == NULL || k == 0)
return NULL;
else
return KthNodeCore(pRoot, k);
}
private:
//中序遍历的第k个结点为所求,中序遍历的时候我们在递归完左子树之后打印根结点,
//本题不是打印,如果左子结点不是要找的结点,才会访问根结点,所以访问到根结点的时候要将k-1
//因为左子结点已经证明不是要找的结点了,排除左子结点。这个过程可以看成目标移位的过程,
//每经过一个结点,k-1,知道k==1,当前节点就是要求的结点。
TreeNode* KthNodeCore(TreeNode* pRoot, int& k){
TreeNode* target = NULL;
if (pRoot->left) target = KthNodeCore(pRoot->left, k);
if (target == NULL){
if (k == 1)
target = pRoot;
k--;
}
if (target == NULL && pRoot->right)
target = KthNodeCore(pRoot->right, k);
return target;
}
};
相似题目
本题与LeetCode中的230. Kth Smallest Element in a BST
完全一致。参考代码见:
LeetCode 230 code
还可以在牛客网 剑指offer上完成对本题的练习。
【参考】
[1] 《剑指offer》
欢迎转载,转载请注明出处: wenmingxing 《剑指offer》树专题