Tensor和自动求导属于PyTorch中较为底层的特性,如果要实现一个神经网络我们不需要从Tensor开始,PyTorch已经为我们封装了专门为深度学习而设计的模块,这个模块就是torch.nn。
NN工具箱
为方便用户使用,PyTorch实现了神经网络中绝大多数的layer,这些layer都继承于nn.Module。这个类封装了可学习参数,并实现了forward函数,且很多都专门针对GPU运算进行了CuDNN优化,其速度和性能都十分优异。
torch.nn.Module:PyTorch中神经网络的基本类,模型和网络层都是它的子类。
class Model(nn.Module):
# 继承nn.Module
def __init__(self, in_features, out_features):
super(Linear, self).__init__()
...
def forward(self, x):
...
torch.nn:PyTorch中的神经网络工具箱,所有的常用神经网络模型都在这个模块中,包括全连接层、卷积层、RNN等。
torch.nn.Linear()
torch.nn.Conv2d()
torch.nn.BatchNorm2d()
...
torch.nn.functional:提供了一些功能的函数化接口,torch.nn中的大多数layer在其中都有一个与之相对应的函数。
# 含参数
torch.nn.functional.linear()
# 不含参数
torch.nn.functional.relu()
torch.nn.functional.max_pool2d()
构建简易的神经网络
torch.nn的核心数据结构是Module,它是一个抽象概念,既可以表示神经网络中的个层(layer),也可以表示一个包含很多层的神经网络。要构造一个神经网络模型,首先我们需要创建一个nn.Module的子类,然后在这个子类中构造我们的模型。
网络
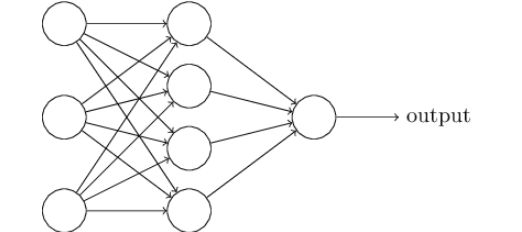
定义一个简单的三层神经网络。
__init__():初始化父类,定义各个层的结构。
forward():根据定义的层,构建向前传播的流程。
from torch import nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(20, 120)
self.fc2 = nn.Linear(120, 64)
self.fc3 = nn.Linear(64, 1)
self.drop = nn.Dropout(0.3)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.drop(x)
x = self.fc3(x)
return x
if __name__ == '__main__':
net = Net()
print(net)
可以打印模型的结构:
Net(
(fc1): Linear(in_features=20, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=64, bias=True)
(fc3): Linear(in_features=64, out_features=1, bias=True)
(drop): Dropout(p=0.3)
)
训练
配置损失函数,因为是回归任务,这里选择的是MSE。
loss_function = nn.MSELoss()
通过torch.optim配置优化器,这里使用的是SGD。optim接受两个参数,第一个是模型的可训练参数net.parameters(),第二个是学习率lr。
import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.001)
对模型进行优化的过程如下所示:
- 首先通过
optimizer.zero_grad()把梯度置零,也就是把loss关于weight的导数变成0。这是因为PyTorch中梯度是累加的,在每个batch中我们不需要前面batch的梯度。 - 根据输入数据得到模型的输出。
- 通过之前定义的
loss_function来计算loss。 - 通过
loss.backward()对loss进行反向传播。 - 通过
optimizer.step()使用之前定义的优化器优化网络。
optimizer.zero_grad()
output = net(inputs)
loss = loss_function(output, target)
loss.backward()
optimizer.step()
保存与载入
PyTorch可以把数据保存为.pth或者.pt等文件。
保存和加载整个模型:
torch.save(net, 'net.pth')
net = torch.load('net.pth')
仅保存和加载模型参数(推荐使用,需要提前手动构建模型):
torch.save(net.state_dict(), 'net.pth')
net.load_state_dict(torch.load('net.pth'))
完整的训练流程
if __name__ == '__main__':
net = Net()
print(net)
x = torch.randn(100, 20)
y = torch.randn(100, 1)
optimizer = optim.SGD(net.parameters(), lr=0.001)
loss_function = nn.MSELoss()
running_loss = 0.0
for i in range(10):
index = torch.randperm(100);
x = x[index]
y = y[index]
b = list(range(0, 100, 10))
for j, b_index in enumerate(b):
inputs = x[b_index: b_index + 10, :]
target = y[b_index: b_index + 10, :]
if torch.cuda.is_available():
inputs = inputs.cuda()
target = target.cuda()
optimizer.zero_grad()
output = net(inputs)
loss = loss_function(output, target)
loss.backward()
optimizer.step()
running_loss += loss.item()
if i != 0 and i % 2 == 0:
print('epoch:{} | batch:{}| loss:{:.5f}'.format(i, j, running_loss / 2))
running_loss = 0.0
torch.save(net.state_dict(), 'net.pth')
训练结果:
...
epoch:6 | batch:7| loss:0.56948
epoch:6 | batch:8| loss:0.50152
epoch:6 | batch:9| loss:0.18269
epoch:8 | batch:0| loss:4.45438
epoch:8 | batch:1| loss:0.20041
epoch:8 | batch:2| loss:0.69559
epoch:8 | batch:3| loss:0.17017
epoch:8 | batch:4| loss:0.29025
epoch:8 | batch:5| loss:0.23748
epoch:8 | batch:6| loss:0.40649
epoch:8 | batch:7| loss:0.36893
epoch:8 | batch:8| loss:0.32532
epoch:8 | batch:9| loss:0.57664
序列模型
nn.Sequential是一个有序的容器,神经网络模块将按照在传入构造器的顺序依次被添加到计算图中执行,同时以神经网络模块为元素的有序字典也可以作为传入参数。对于没有分支的网络结构,使用序列的方法构建模型更加容易。
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.seq = nn.Sequential(
nn.Conv2d(3, 64, 7, 2, 3, bias=False),
nn.BatchNorm2d(64),
nn.ReLU(inplace=True),
nn.MaxPool2d(3, 2, 1)
)
def forward(self, x):
x = self.seq(x)
return x
if __name__ == '__main__':
net = Net()
print(net)
可以看出,多个不同的网络层被一个Sequential类包裹了。
Net(
(seq): Sequential(
(0): Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
(1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(2): ReLU(inplace)
(3): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
)