5.1 仿射变换
5.1.1 仿射变换基础
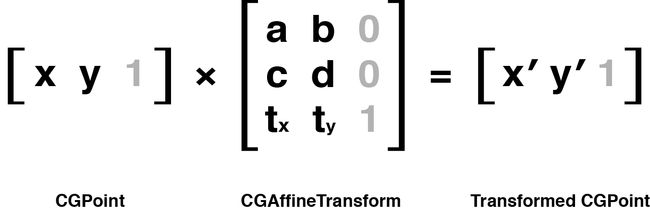
UIView的transform属性是一个CGAffineTransform类型,用于在二维空间做旋转,缩放和平移。CGAffineTransform是一个可以和二维空间向量(例如CGPoint)做乘法的3X3的矩阵
如图所示,通过矩形的相乘运算,得到一个新的CGPoint类型的结果。图中的灰色元素是为了矩形做乘法而添加的辅助标志值,因为他并不改变结果,所以得到的新值中不会保存它,它的用处就是做矩形相乘运算。
当对图层应用变换矩阵,图层矩形内的每一个点都被响应地做变换,从而形成一个新的四边形的形状。CGAffineTransform中的”仿射”的意思是无论变换举证用什么值,图层中平行的两条线在变换之后仍然保持平行,CGAffineTransform可以做出任意符合上述标注的变换。
由矩阵的乘法规则,可得:
x’ = a*x + c*y + tx;
y’ = b*x + d*y + ty;
(1) 让a、d=1 其余均为0,得到 x’ = x , y’ = y。这就是CGAffineTransformIdentity(未发生变换,单位矩阵)
(2) 平移: 让a、d=1,b、c=0,得到x’ = x + tx,y’ = y + ty,可以知道tx代表视图沿x轴方向的位移,ty代表视图沿y轴方向的位移,代码如下:
CGAffineTransformMakeTranslation(CGFloat tx, CGFloat ty)
所以平移矩阵为
(3) 旋转的公式比较复杂,涉及到平面向量的旋转,这里是讲解:平面向量旋转
2D旋转的公式如下:
x’ = x*cos(a) - y*sina(a);
y’ = x*sina(a) - y*cos(a);
可以反推导出旋转的矩阵:
代码如下:
CGAffineTransformMakeRotation(CGFloat angle);
参数只有一个角度,而不是旋转公式里面的cosa,sina,原因就是不管正弦还是余弦,变化的量只是角度a,所以这里的变换函数就提供一个角度了,调用之后系统在函数里就把角度angle转化成相对应的正弦余弦值,再把计算后的矩阵(也就是CGAffineTransform结构体)返回给你了.
angle参数为弧度值,而不是角度值,弧度用数学常量PI的倍数表示,一个PI表示180°。C的数学函数库中提供了弧度的一些简便的换算,如果对换算不太清楚的话,可以用如下的宏做换算:
//将弧度值转化为角度值,参数x为弧度值
#define RADIANS_TO_DEGREES(x) ((x)/M_PI*180.0)
//将角度值转化为弧度制,参数x为角度值
#define DEGREES_TO_RADIANS(x) ((x)/180.0*M_PI)
(4)放缩:让除了a、d外,其它参数都等于0,则得到放缩公式:
x’ = a*x;
y’ = d*y;
所以缩放矩阵为:
代码如下:
CGAffineTransformMakeScale(CGFloat sx, CGFloat sy)
其它用法:
//检查是否有做过仿射效果
CGAffineTransformIsIdentity(transform)
//检查2个仿射效果是否相同
CGAffineTransformEqualToTransform(transform1,transform2)
//仿射效果反转(反效果,比如原来扩大,就变成缩小)
CGAffineTransformInvert(transform)
总结
CGAffineTransform本质就是一个结构体,这个结构体代表一个3*3的矩阵.由于矩阵第三列始终是固定的(0,0,1),所以这个结构体只有6个元素.
将一个代表2D变换的矩阵CGAffineTransform设置给view.transform,系统就会在内部让[x,y,1]和这个矩阵进行乘法运算,最终得到变换后的座标x’,y’,从而实现2D变换.
2D图像变换也称2D仿射变换,主要就是放大,缩小,平移,旋转,这几种变换的参数只涉及到矩阵的1,2列的数据,第三列始终都是0,0,1.
5.1.2 ios与安卓的transform图形变换矩阵之间的快速转换方法
首先,为了实现快速的转换,我们必须了解两者之间的异同。 iOS: IOS的Transform matrix 形式是这样的:
a b 0
c d 0
tx ty 1
其中,
a :缩放X b :错切Y 0
c :错切X d :缩放Y 0
tx:位移X ty:位移Y 0
当进行位图片操作的时候,假设元像素点坐标为(x,y,1) 则:
|a b 0|
(x,y,1)*|c d 0| =(ax + by +tx,bx + dy + ty,1)
|tx ty 1|
当进行变换时,根据具体需求,分别改动对应矩阵的对应值,就可以实现想要的效果了,这些实现都被IOS封装到了Transform类方法之中了
Android Android的Transform matrix 形式是这样的:
a c tx
b d ty
0 0 1
其中,
a :缩放X c :错切X tx:位移X
b :错切Y d :缩放Y ty:位移Y
0 0 1
当进行位图片操作的时候,假设元像素点坐标为(x,y,1) 则:
|a c tx| |x|
|b d ty|* |y|=(ax + by +tx,bx + dy + ty,1)
|0 0 1 | |1|
由此不难看出,IOS和Android的Transformation Matrix 是互为转置矩阵关系。所以我们有算法:
for( int k = 0; k < 9; k++){
int n = (k % 3) * 3 + k / 3;
matrix[k] = matrix[k] + matrix[n];
matrix[n] = matrix[k] - matrix[n];
matrix[k] = matrix[k] - matrix[n];
}
来实现两者之间的转换。 使用时,将此算法嵌入到程序中即可。
5.1.3 图层的仿射变换
CALayer同样也有一个transform属性,但它的类型是CATransform3D,而不是CGAffineTransform。CALayer对应于UIView的transform属性叫做affineTransform。
5.1.4 混合变换
Core Graphics提供了一系列的函数可以在一个变换的基础上做更深层次的变换,如果做一个多次的变换的话,这就会非常有用。
多次变换要使用这些函数:
CGAffineTransformRotate(CGAffineTransform t, CGFloat angle)
CGAffineTransformScale(CGAffineTransform t, CGFloat sx, CGFloat sy)
CGAffineTransformTranslate(CGAffineTransform t, CGFloat tx, CGFloat ty)
当操纵一个变换的时候,初始生成一个什么也不做的变换很重要,也就是创建一个CGAffineTransform类型的控制,矩阵中称作单位矩阵,Core Graphics同样也提供了一个方便的常量: CGAffineTransformIdentity
注意:在混合变换中,多次的变换如果其中的顺序改变,可能会改变最终的结果,也就是说,上一个变换的结果将会影响以后的变换,所以,在混合变换中,对顺序的控制是很重要的
5.2 3D变换
5.2.1 3D变换
CGAffineTransform类型属于Core Graphics框架,它是一个严格意义上的2D绘图API,并且CGAffineTransform仅仅对2D变换有效。
CALayer有一个zPosition属性,它的transform属性可以做到让图层靠近或者原理相机,即让图层在3D控件内移动或者旋转。
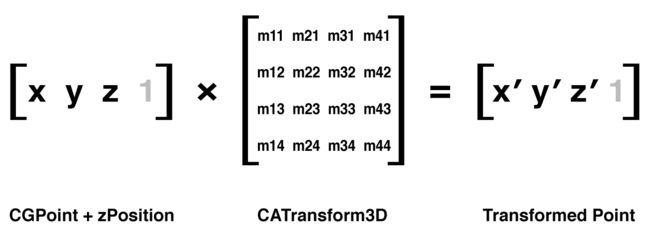
和CGAffineTransform矩阵类似,Core Animation提供了一系列的方法用来创建和组合CATransform3D类型的矩阵,和Core Graphics的函数类似,但是3D的平移和旋转多出了一个z参数,并且旋转函数除了angle之外多出了x,y,z三个参数,分别决定了每个坐标轴方向上的旋转。
CATransform3DMakeRotation(CGFloat angle, CGFloat x, CGFloat y, CGFloat z)
CATransform3DMakeScale(CGFloat sx, CGFloat sy, CGFloat sz)
CATransform3DMakeTranslation(Gloat tx, CGFloat ty, CGFloat tz)
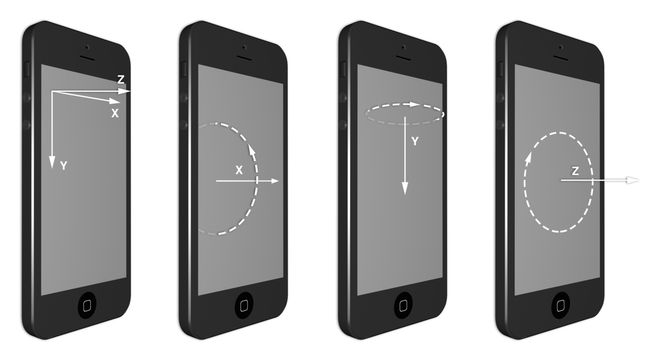
我们对X轴和Y轴比较熟悉了,分别以右和下为正方向(在Mac OS上,Y轴向上为正方向),Z轴和这两个轴分别垂直,指向视图外为正方形。
由图所见,绕Z轴旋转等同于之前二维空间的仿射旋转,但是绕X轴和Y轴的旋转就突破了屏幕的二维空间,并且在用户视角看来发生了倾斜。
如果我们通过代码使得图层绕着X轴或者Y轴旋转,看起来图层并没有被旋转,而是仅仅在垂直/水平方向上产生了压缩,其实这是没错的,视图看起来更窄实际上是因为我们在用一个斜向的视角看它,而不是透视。
5.2.2 透视投影
真实世界中,当物体远离我们的时候,由于视角的原因看起来会变小,理论上说远离我们的视图的边要比靠近视角的边更短,但实际上并不一定,而我们当前的视角是等距离的,也就是在3D变换中仍然保持平行,和之前提到的仿射变换类似。
在等距投影中,远处的物体和近处的物体保持同样的缩放比例,这种投影也有它自己的用处,但当前我们并不需要。
为了做一些修正,我们需要引入投影变换(又称作z变换)来对除了旋转之外的变换矩阵做一些修改,Core Animation并没有给我们提供设置透视变换的函数,因此我们需要手动修改矩阵值,幸运的是,很简单:
CATransform3D的透视效果通过一个矩阵中一个很简单的元素来控制:m34。m34用于按比例缩放X和Y的值来计算到底要离视角多远。
m34的默认值是0,我们可以通过设置m34为-1.0/d来应用透视效果,d代表了想象中视角相机和屏幕之间的距离,以像素为单位,那应该如何计算这个距离呢?实际上并不需要,大概估算一个就好了。
因为视角相机实际上并不存在,所以可以根据屏幕上的显示效果自由决定它放置的位置。通常500-1000就已经很好了,但对于特定的图层有时候更小或者更大的值会看起来更舒服,减少距离的值会增强透视效果,所以一个非常微小的值会让它看起来更加失真,然而一个非常大的值会让它基本失去透视效果。
5.2.3 灭点
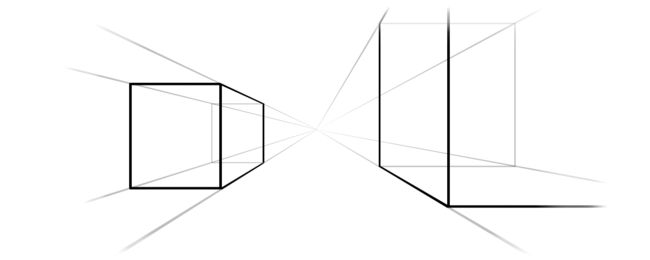
当在透视角度绘图的时候,远离视角的物体会变小边缘,当远离到一个极限距离,他们可能就缩成了一个点,于是所有的物体最后都汇聚消失在同一个点。
在现实中,这个点通常是视图的中心,于是为了在应用中穿件拟真效果的透视,这个点应该聚在屏幕中点,或者至少是包含所有3D对象的视图中点。
5.2.4 sublayerTransform属性
如果有多个视图或者图层,每个都做3D变换,那就需要分别设置相同的m34值,并且确保在变换之前都在屏幕中央共享同一个position,如果用一个函数封装这些操作的确会更加方便,但仍然有限制。
CALayer有一个属性叫做sublayerTransform,它也是CATransform3D类型,但和对一个图层的变换不同,它能影响所有的子图层。这意味着你可以一次性对包含这些图层的容器做变换,于是所有的子图层都自动继承了这个变换方法。
相比较而言,通过在一个地方设置透视变换会很方便,同时它会带来另一个显著的优势:灭点被设置在容器图层的中点,从而不需要再对子图层分别设置了。这意味着你可以随意使用position和frame来设置子图层,而不需要把它们放置在屏幕中点,然后为了保证统一的灭点用变换来做平移。
CATransform3D perspective = CATransform3DIdentity;
perspective.m34 = - 1.0 / 500.0;
self.containerView.layer.sublayerTransform = perspective;
//rotate layerView1 by 45 degrees along the Y axis
CATransform3D transform1 = CATransform3DMakeRotation(M_PI_4, 0, 1, 0);
self.layerView1.layer.transform = transform1;
//rotate layerView2 by 45 degrees along the Y axis
CATransform3D transform2 = CATransform3DMakeRotation(-M_PI_4, 0, 1, 0);
self.layerView2.layer.transform = transform2;
5.2.5 背面
我们既然可以在3D场景下旋转图层,那么也可以从背面去观察它。如果我们把相对y轴的旋转角度设置为M_PI(π,180°),那么将会把图层完全旋转一个半圈,于是图层完全背对了相机视角。
如图所示,图层是双面绘制的,反面显示的是正面的一个镜像图片。
CALayer有一个叫做doubleSided的属性来控制图层的背面是否要被绘制,这是一个BOOL类型,默认为YES,如果设置为NO,那么当图层正面从相机角度消失的时候,它将不会被绘制。(如果在不需要看到背面的时候,我们可以设置这个属性为NO,那么就不用浪费GPU来绘制它)
5.2.6 扁平化图层
Core Animation创建非常复杂的3D场景是非常困难的。你不能够使用图层树去创建一个3D结构的层级关系—在相同场景下的任何3D表面必须和同样的图层保持一致,这是因为每个的父视图都把它的子视图扁平化了。
至少当你用正常的CALayer的时候是这样,CALayer有一个叫做CATransformLayer的子类来解决这个问题。
5.3 固体对象
5.3.1 固体对象
现在你懂得了在3D空间的一些图层布局的基础,我们可以试着创建一个固态的3D对象(实际上是一个技术上所谓的空洞对象,但它以固态呈现)。我们用六个独立的视图来构建一个立方体的各个面。
Demo
旋转这个立方体将会显得很笨重,因为我们要单独对每个面做旋转,另一个简单的方案是通过调整容器视图的sublayerTransform去旋转照相机。
perspective = CATransform3DRotate(perspective, -M_PI_4, 1, 0, 0);
perspective = CATransform3DRotate(perspective, -M_PI_4, 0, 1, 0);