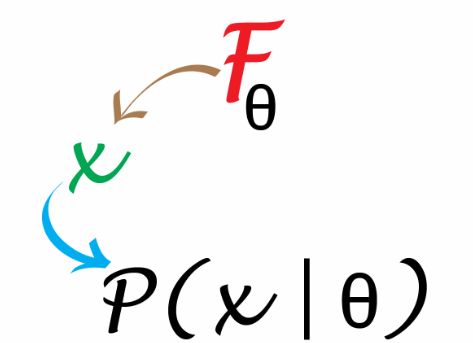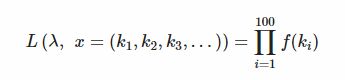《Modern Statistics for Modern Biology》Chapter 一: 离散数据模型的预测(1.1 - 1.3)
《Modern Statistics for Modern Biology》Chapter 一: 离散数据模型的预测(1.4 - 1.5)
- 在第一章中,关于生成模型和参数值的知识为我们提供了可以下结论的可能性-例如,我们是否真的找到了一个表位。在许多实际情况下,生成模型和参数都是未知的,我们需要使用收集到的数据来估计它们。统计建模从数据向上(upwards)到可能合理地解释数据的模型,即使我们找到了一个能够完美地解释我们当前所有数据的模型,但现实可能总是更加复杂。通过一组新的数据,我们可以得出需要另一个模型的结论,并且可以将当前模型作为特例或近似值包括在内。这种向上推理的步骤称为统计推断(下图)。本章将向我们展示作为推理构建块的一些分布和评估机制。尽管本章中的例子都是参数化的(即统计模型只有少量未知参数),但我们讨论的原理将得到推广。
2.1 本章的目标
在这一章我们将学到以下知识
分清楚经常被混淆的两个主题之间是有区别的:“概率”和“统计”。
使用直方图和其他可视化技巧使数据符合概率分布
通过模拟实验第一次遇到一种称为最大似然的估计过程
从我们有先验信息的数据中进行推断。为此,我们将使用贝叶斯范例,它将涉及具有特殊定制属性的新发行版。我们将使用模拟,看看贝叶斯估计与最大似然的简单应用有何不同。
使用统计模型和估计来评估二项分布和多项分布中的相依性。
分析一些历史上有趣的基因组数据汇编成表格。
建立相依数据的马尔可夫链模型。
做一些具体的应用,计算全基因组中的基序(motif),并学会专门用于基因组数据分析的特殊
Bioconductor包。、
参数是关键(Parameters are the key.)
- 我们在第一章中看到,对表位例子中所有参数值的了解使我们能够使用我们的概率模型,并根据我们手头的数据来检验一个零假设。通过一些真实的例子和计算机模拟,我们将看到不同的统计建模方法,但让我们首先根据可用信息的多少对两种情况进行区分。
2.2 统计模型和概率模型的区别
当我们知道一个好的数据随机性的生成模型,并且我们得到了参数的实际值时,概率分析就成为可能。
在表位的例子中,由于知道每个位置的伯努利(0.01)出现假阳性,检测的患者数量和蛋白质的长度确保了没有任何未知的参数。
-
在这种情况下,我们可以使用数学推导来计算事件的概率,如图 2.1所示。在表位的例子中,我们使用泊松概率作为零模型,并给出了参数
λ=0.5时的零模型。我们可以通过数学推导得出结论,看到最大值7或更大的概率大约在10−4左右,因此实际上在该模型(或“零假设”)下观测到的数据是极不可能的。
现在,假设我们知道病人的数量和蛋白质的长度(这是由实验设计给出的),但不知道分布本身和假阳性率。一旦我们观察到数据,我们需要从数据向上去估计一个概率模型F(泊松,正态,二项),并最终估计该模型的
缺失参数。这就是我们将在本章中解释的统计推断的类型。
2.3 统计建模的一个简单例子
从数据开始
建模过程分为两个部分。首先,我们需要一个合理的概率分布来模拟数据生成过程。正如我们在第一章中看到的,离散的计数数据可以用简单的概率分布建模,如二项分布、多项分布或泊松分布。正态分布,或钟形曲线,往往是一个很好的模型,连续测量。分布也可以是这些基本分布的更复杂的混合(在第4章中将更详细地介绍这一点)。
让我们重新审视上一章中的表位示例,开始时不会出现棘手的离群点。
setwd("E:/compute language/NGS/Modern Statistics for Modern Biology/data")
load("e100.RData")
e99 = e100[-which.max(e100)]
拟合优度:可视化评估
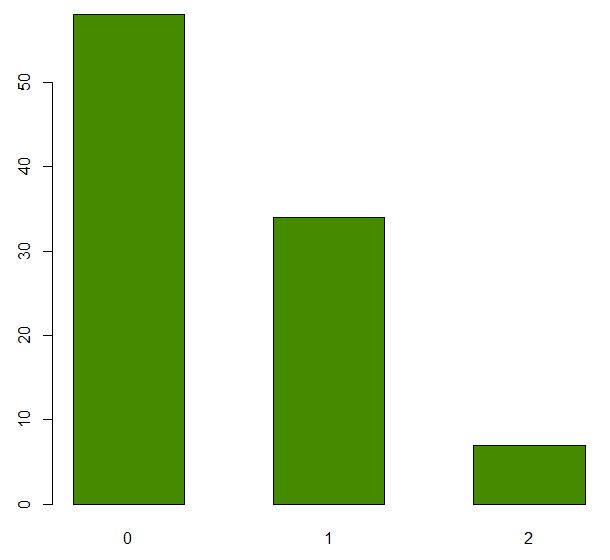
- 我们的第一步是从候选分布中找到拟合;这需要咨询图形化和定量的拟合优度图。对于离散数据,我们可以绘制一个频率条形图(对于连续数据,我们可以查看直方图),如图2.2所示。
barplot(table(e99), space = 0.8, col = "chartreuse4")
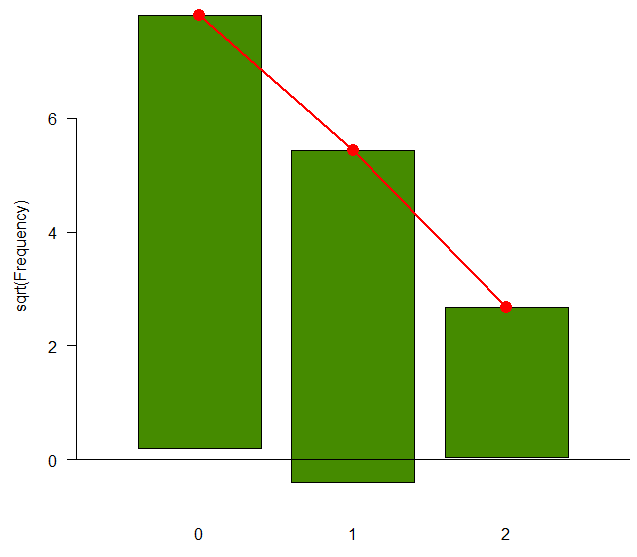
- 但是,如果不进行比较,很难确定哪种理论分布最适合数据。一种视觉拟合优度图被称为
rootogram;它挂着从理论红点观察到的计数的条形图。如果计数与其理论值完全对应,则长方体底部将与水平轴精确对齐。
library("vcd")
gf1 = goodfit( e99, "poisson")
rootogram(gf1, xlab = "", rect_gp = gpar(fill = "chartreuse4"))
► 问题 2.1
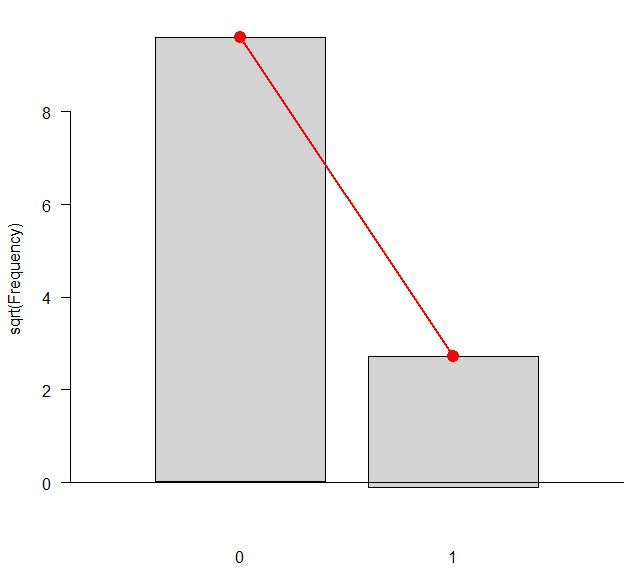
- 要用已知的泊松变量校准这样的图,请使用
rpois函数以λ=0.0 5的生成100个泊松分布数并绘制它们的示意图。
► 答案
simp = rpois(100, lambda = 0.05)
gf2 = goodfit(simp, "poisson")
rootogram(gf2, xlab = "")
我们看到,
e99的路标似乎相当符合泊松模型。但是请记住,为了实现这一点,我们删除了异常值。泊松完全由一个参数决定,通常称为泊松平均λ。在大多数情况下,我们可以猜测数据服从泊松分布,我们需要从数据中估计泊松参数。-
估算
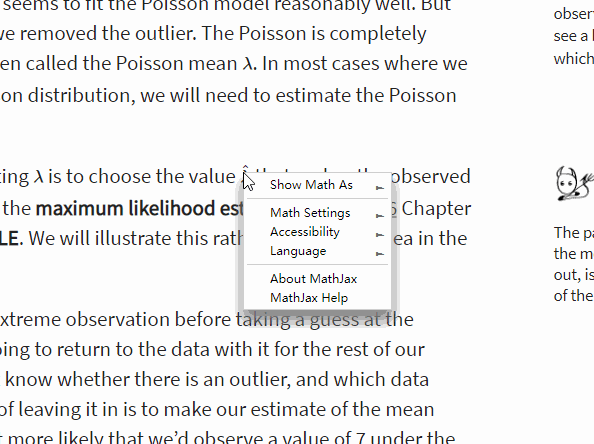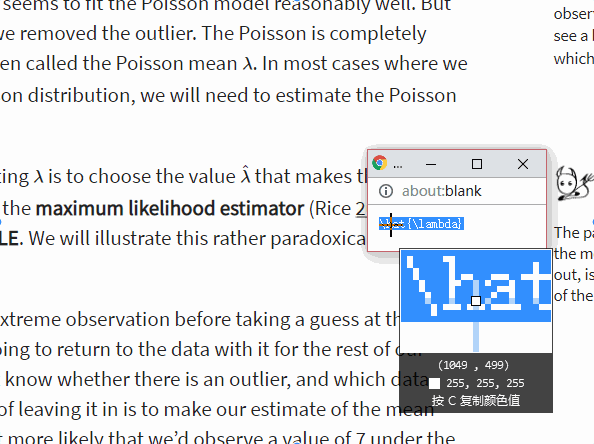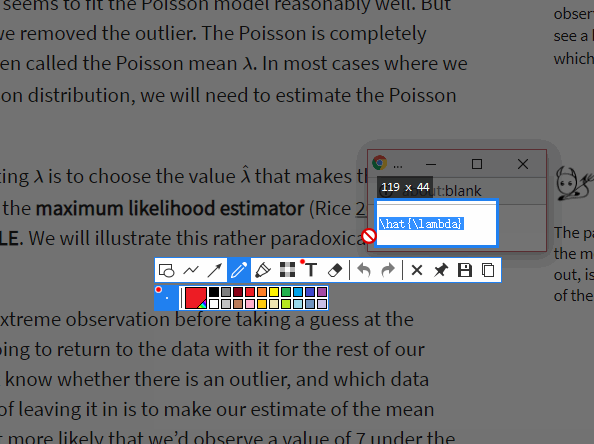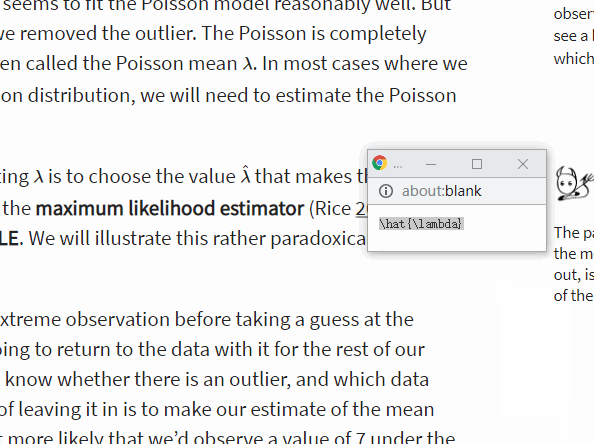
λ最常用的方法是选择使观测数据最有可能出现的值(插一句,这教程真的很nice,比如这个表达式我就是直接copy他的latex格式来的)。这被称为极大似然估计(Rice 2006,第8章,第5节),通常缩写为MLE。我们将在下一节中说明这一自相矛盾的观点。
虽然我们在猜测概率分布之前进行了极端的观察,但我们将返回到数据,然后再进行其余的分析。在实践中,我们不会知道是否存在离群点,以及它是/它们是哪个数据点。把它放进去的效果是使我们对平均数的估计更高。反过来,这将使我们更有可能在
零假设模型下观察值7,从而导致更大的p值。因此,如果结果的p值很小,即使包含了离群值,我们也可以确信我们的分析是真实的。我们称这种策略是保守的:我们在谨慎的一边犯了错误,因为我们没有发现什么东西。
泊松分布参数的估计
- 泊松平均值的什么值使数据最有可能?第一步,我们统计结果。
> table(e100)
e100
0 1 2 7
58 34 7 1
- 然后,我们将尝试不同的泊松平均值,看看哪一个最适合我们的数据。如果泊松分布的平均λ为3,则计数如下所示:
> table(rpois(100, 3))
0 1 2 3 4 5 6 9
7 16 27 18 19 7 5 1
- 比我们在数据中看到的还要多的2和3。因此,我们看到
λ=3不太可能产生我们的数据,因为计数不太匹配。
► 问题 2.2
使用不同的λ值重复此模拟。你能找到一种只通过反复试验就能给出与观察到的结果接近的计数的方法吗?
-
因此,我们可以尝试许多可能的价值,并进行蛮力。然而,我们将做一些更优雅的事情,并使用一些数学来看看哪个值最大限度地提高了观察数据的可能性。如果泊松参数的值是m,我们来计算看到数据的概率。因为我们假设数据来自独立的绘图,所以这个概率只是单个概率的乘积:
当
m = 3时, 我们可以使用R这样计算
> prod(dpois(c(0, 1, 2, 7), lambda = 3) ^ (c(58, 34, 7, 1)))
[1] 1.392143e-110
► 问题2.3
- 计算
m=0,1,2的概率。m必须是整数吗?例如,尝试计算m=0.4的概率
> prod(dpois(c(0, 1, 2, 7), lambda = 0) ^ (c(58, 34, 7, 1)))
[1] 0
> prod(dpois(c(0, 1, 2, 7), lambda = 1) ^ (c(58, 34, 7, 1)))
[1] 5.766487e-50
> prod(dpois(c(0, 1, 2, 7), lambda = 2) ^ (c(58, 34, 7, 1)))
[1] 7.728814e-77
> prod(dpois(c(0, 1, 2, 7), lambda = 0.4) ^ (c(58, 34, 7, 1)))
[1] 8.5483e-46
► 解
-
这个概率是λ的似然函数,给定数据,写作如下:
它不是用100个小数的乘法运算,采用这种算法是很方便地。取对数。由于对数是严格递增的,如果对数在一个区间内达到最大值,它也将是概率的最大值。
让我们从一个计算性的例子开始。我们计算了泊松参数的许多不同值的似然。要做到这一点,我们需要编写一个小函数来计算不同值的数据的概率。
loglikelihood = function(lambda, data = e100) {
sum(log(dpois(data, lambda)))
}
- 现在我们可以计算一系列
lambda值从0.05到0.95的可能性(图 2.4)。
> lambdas = seq(0.05, 0.95, length = 100)
> loglik = vapply(lambdas, loglikelihood, numeric(1))
> plot(lambdas, loglik, type = "l", col = "red", ylab = "", lwd = 2,
+ xlab = expression(lambda))
> m0 = mean(e100)
> abline(v = m0, col = "blue", lwd = 2)
> abline(h = loglikelihood(m0), col = "purple", lwd = 2)
> m0
[1] 0.55
► 问题 2.4
vapply在这里发挥什么样的功能vapply()它需要显式地指明所希望简化为的具体格式,如果无法简化为所指定的格式,则会给出Error。vapply()比sapply()更加“保险”,你总能通过vapply()得到希望的结果(或者Error)。此外,在大量数据下使用vapply()的效率要比sapply()高,因为vapply()不需要像sapply()那样去猜测如何对结果进行合适的简化。
R语言中vapply()和tapply()的用法
► 解
- 事实上,有一种快捷方式:函数
goodfit。
> gf = goodfit(e100, "poisson")
> names(gf)
[1] "observed" "count" "fitted" "type" "method" "df"
[7] "par"
> gf$par
$`lambda`
[1] 0.55
-
goodfit的输出是一个称为list的复合对象。它的一个组成部分称为par,包含所研究的分布的拟合参数的值。在这种情况下,它只是一个数字,λ的估计。
► 问题 2.5
-
goodfit函数的输出的其他组件是什么?
goodfit本质上是计算离散分布(泊松分布、二项分布或负二项分布)在x中给出的计数数据的拟合值。如果未指定参数,则用ML或最小x平方估计它们。
要确定参数:par是一个指定参数lambda的命名列表,分别指定“泊松”的参数lambda和“二项”或“正态”的prob和size。如果为“二项式”,则不指定大小,
而是将其视为最大计数。
-
observed: 观察频率 -
count: 对应的数量 -
fitted: 预期的频率(ML来拟合) -
type: 表示拟合分布的字符串类型 -
method: 指示拟合方法的字符串(如果指定了参数,则可以是“ML”、“MinChisq”或“fixed”)。 -
df: 自由度 -
par: (估计的)分布参数的命名列表
- 将m的值与我们以前为λ使用的值进行比较。用m重做我们在第1章中所做的建模,而不是用0.5。
......未完待续.....。