之前对前端的算法和数据结构做了一些寻章摘句的部分零散的总结和归纳,详见《前端算法与数据结构自学总结(实战篇)》和《前端算法与数据结构自学总结(理论篇)》,其实也就是把遇到的问题总结了一下。
这次想系统的学习一下,在这个过程中去学习思考,会慢慢更新。从基础字符串、数组、正则和常用排序算法,到数据结构的堆栈、队列、二叉树等,再到高级算法的动态规划、贪心算法、回溯算法等做一次比较全面的巩固和归纳总结。
一、字符串
1、反转字符串中的单词
给定一个字符串,你需要反转字符串中每个单词的字符顺序,同时仍保留空格和单词的初始顺序。
输入: "Let's take LeetCode contest"
输出: "s'teL ekat edoCteeL tsetnoc"
注意:在字符串中,每个单词由单个空格分隔,并且字符串中不会有任何额外的空格。
分析:这个其实就是字符串中每个单词的反转,能联想到数组的reverse方法,同时数组和字符串的相互转化的方法split()和join()。
const reverseWords = function(s) {
const arr = s.split(" ");
const result = arr.map(item =>item = item.split("").reverse().join(""));
return result.join(" ");
};
算法的本质是寻找规律并实现
发现输入和输出的关系,寻找突破点
实现是程序+数据结构的结合体
2、计数二进制子串
给定一个字符串s,计算具有相同数量0和1的非空(连续)子字符串的数量,并且这些子字符串中的所有0和所有1都是组合在一起的。
重复出现的子串要计算它们出现的次数。
- 示例 1 :
输入: "00110011"
输出: 6
解释: 有6个子串具有相同数量的连续1和0:“0011”,“01”,“1100”,“10”,“0011” 和 “01”。
请注意,一些重复出现的子串要计算它们出现的次数。
另外,“00110011”不是有效的子串,因为所有的0(和1)没有组合在一起。
- 示例 2 :
输入: "10101"
输出: 4
解释: 有4个子串:“10”,“01”,“10”,“01”,它们具有相同数量的连续1和0。
注意:s.length 在1到50,000之间。s 只包含“0”或“1”字符。
方法一
/**
* @param {string} s
* @return {number}
*/
const countBinarySubstrings = function(s) {
const result = [];
// 返回一个符合条件的子串
const match = (str) => {
// 0或1开头的连续字符串
const j = str.match(/^(0+|1+)/)[0];
// js的未操作符 取反, 结果是一个Number型
let k = (j[0] ^ 1);
// 转为字符串,且长度k与j保持一样
k = k.toString().repeat(j.length);
const reg = new RegExp(`(${j}${k})`);
if (reg.test(str)) {
// 返回符合正则的第一个子匹配
return RegExp.$1;
} else {
return "";
}
}
for (let i = 0, len = s.length - 1; i < len; i++) {
const subStr = match(s.slice(i));
if (subStr) {
result.push(subStr);
}
}
return result.length
};
主要考察字符串的slice, match, test, 以及常用的正则表达式RegExp。
但是上面这个方法,当给定的字符串长度过长时,正则表达式会报错"RegExp too big",导致程序运行失败,那么还可以选择下面的方法:
方法二
/**
* @param {string} s
* @return {number}
*/
const countBinarySubstrings = function(s) {
// 当前字符连续数(至少1个)
let curCharLength = 1
// 上一个字符的连续数
let perCharLength = null
let count = 0
for(let i=0;i如:"110001100111", 分割为 "11", "000", "11", "00", "111"
可以取["11", "000"], ["000", "11"], ["11", "00"], ["00", "111"]
这样,取每个分组下最小的字符串长度,最后加起来就是符合要求的子串总数。
二、数组
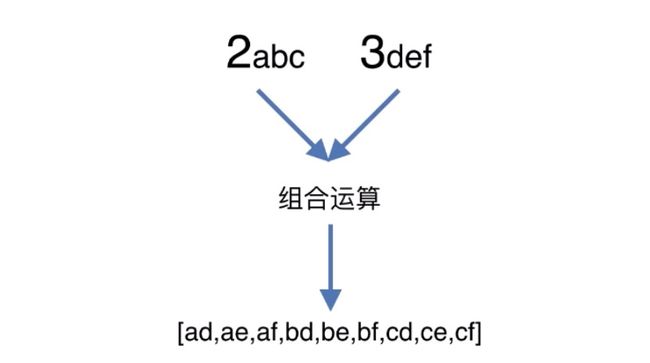
1、电话号码组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例:
输入:"23"
输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
分析:2个以上的数字组合的时候,先2个组成一个数组,将结果当成一个数字去和下一个组合,以此类推。这样就可以用递归的方式,两两组合运算。伪代码思路如下:
// 伪代码
const result = []
for(i=0; i 1) {
// 递归
} else {
return result
}
全部代码如下:
/**
* @param {string} digits
* @return {string[]}
*/
var letterCombinations = function(digits) {
if (digits.length < 1) {
return []
}
// 建立电话号码的映射关系
const map = ['', 1, 'abc', 'def', 'ghi', 'jkl', 'mno', 'pqrs', 'tuv', 'wxyz'];
if (digits.length < 2) {
return map[digits].split('');
}
// 把输入的数字分割成数组
const nums = digits.split('');
// 将输入的数字转换为映射的字母组合,如 23=>['abc','def']
const codes = [];
nums.map(item => {
// 排除输入的0对应的空
if (map[item]) {
codes.push(map[item]);
}
});
// 递归函数
const foo = (arr) => {
const temp = [];
// 循环遍历第一项和第二项
for(let i = 0; i < arr[0].length; i++) {
for(let j = 0; j < arr[1].length; j++) {
temp.push(`${arr[0][i]}${arr[1][j]}`);
}
}
// 用新的组合代替前两项
arr.splice(0, 2, temp);
// 开始递归
if (arr.length > 1) {
foo(arr);
} else {
return temp;
}
// 最终直到arr只有一项为止,直接返回这一项
return arr[0];
}
return foo(codes);
};
2、种花问题
假设你有一个很长的花坛,一部分地块种植了花,另一部分却没有。可是,花卉不能种植在相邻的地块上,它们会争夺水源,两者都会死去。
给定一个花坛(表示为一个数组包含0和1,其中0表示没种植花,1表示种植了花),和一个数 n 。能否在不打破种植规则的情况下种入 n 朵花?能则返回True,不能则返回False。
示例如下:
输入: flowerbed = [1,0,0,0,1], n = 1
输出: True
输入: flowerbed = [1,0,0,0,1], n = 2
输出: False
代码如下:
/**
* @param {number[]} flowerbed
* @param {number} n
* @return {boolean}
*/
var canPlaceFlowers = function(flowerbed, n) {
// 设置一个计数器
let max = 0;
for (let i = 0; i < flowerbed.length -1; i ++) {
// 当花坛中是空地0才去判断,否则已种花的直接跳过不管
if (flowerbed[i] === 0) {
// 如果是第一个元素,且当前元素是0
if (i === 0 && flowerbed[1] === 0) {
max++;
i++;
} else if (flowerbed[i - 1] === 0 && flowerbed[i + 1] === 0) {
max++;
i++;
}
}
}
// 是否能种下n朵花,返回true或false
return max >= n;
};
三、正则表达式
1、重复的子字符串
给定一个非空的字符串,判断它是否可以由它的一个子串重复多次构成。
给定的字符串只含有小写英文字母,并且长度不超过10000。
示例如下:
输入: "abab"
输出: True
解释: 可由子字符串 "ab" 重复两次构成。
输入: "abcabcabcabc"
输出: True
解释: 可由子字符串 "abc" 重复四次构成。 (或者子字符串 "abcabc" 重复两次构成。)
分析:
- 首先标记一个子表达式,需要有一个括号
(),称为捕获括号; - 然后写一个单字字符
\w,因为不确定子串字符长度,所以至少匹配一次\w+,加号+表示子表达式一次或多次,此处\w+表示多个字母的一次组合; - 那么一组字符串出现多次,可以用
\1+表示出现2次及以上的重复; - 最后还要加入起始的限定
^和$,这样就构成了一个正则/^(\w+)\1+$/。
代码如下:
/**
* @param {string} s
* @return {boolean}
*/
var repeatedSubstringPattern = function(s) {
const reg = /^(\w+)\1+$/
return reg.test(s)
};
三、排序
1、冒泡排序
时间复杂度: O(n^2)
- 算法描述:
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
5 6 3 1 8 7 2 4
[5 6] 3 1 8 7 2 4 //比较5和6
5 [6 3] 1 8 7 2 4
5 3 [6 1] 8 7 2 4
5 3 1 [6 8] 7 2 4
5 3 1 6 [8 7] 2 4
5 3 1 6 7 [8 2] 4
5 3 1 6 7 2 [8 4]
5 3 1 6 7 2 4 8 // 这样最后一个元素已经在正确位置,所以下一次开始时候就不需要再比较最后一个
- 代码思路:
外循环控制需要比较的元素,比如第一次排序后,最后一个元素就不需要比较了,内循环则负责两两元素比较,将元素放到正确位置上。
function bubbleSort(arr){
for(let i = arr.length - 1; i > 0; i--){
for(let j = 0; j < i; j++){
if(arr[j] > arr[j+1]){
const tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp
}
}
}
return arr;
}
2、选择排序
时间复杂度:O(n^2)
- 算法描述:直接从待排序数组中选择一个最小(或最大)数字,放入新数组中。
[1] 5 6 3 8 7 2 4
[1,2] 5 6 3 8 7 4
[1,2,3] 5 6 8 7 2 4
[1,2,3,4] 5 6 8 7
[1,2,3,4,5] 6 8 7
[1,2,3,4,5,6] 8 7
[1,2,3,4,5,6,7] 8
[1,2,3,4,5,6,7,8]
` 代码思路:
先假设第一个元素为最小的,然后通过循环找出最小元素,然后同第一个元素交换,接着假设第二个元素,重复上述操作即可。
function selectSort (arr) {
for (let i = 0; i < arr.length; i++){
let min = arr[i]; // 假定一个最小值
for (let j = i + 1; j < arr.length; j++) {
// 循环选出最小的
if (arr[j] < min) {
let temp = min;
min = arr[j];
arr[j] = temp;
}
}
arr[i] = min;
}
return arr;
}
3、按奇偶排序数组
给定一个非负整数数组 A, A 中一半整数是奇数,一半整数是偶数。
对数组进行排序,以便当 A[i] 为奇数时,i 也是奇数;当 A[i] 为偶数时, i 也是偶数。
你可以返回任何满足上述条件的数组作为答案。
示例:
输入:[4,2,5,7]
输出:[4,5,2,7]
解释:[4,7,2,5],[2,5,4,7],[2,7,4,5] 也会被接受。
代码:
/**
* @param {number[]} arr
* @return {number[]}
*/
var sortArrayByParityII = function(arr) {
arr.sort((a, b) => a - b); // 降序排列
const newArr = []; // 申请一个新数组,用来存储排序后的数组
let odd = 1; // 记录奇数下标
let even = 0; // 记录偶数下标
arr.forEach(item => {
if (item % 2 === 1) {
newArr[odd] = item; // 如果是奇数
odd += 2;
} else {
newArr[even] = item; // 如果是偶数
even += 2;
}
});
return newArr;
};