Log
- 【170407】完成了 Python 版代码的书写(01,02)
- 【170408】进行了一次优化,完成了 Python 版代码的书写(03)
- 【170409】完成了 02 版 Python 代码到 C++ 代码的翻译(04);完成了 03 版 Python 代码到 C++ 代码的翻译(05)
题目
Two Sum II
【题目类型备注】
二分查找, 哈希表, 双指针
提交
01
【语言】
Python
【时间】
170407
【思路】
〖复杂度?〗可能是和 logn 有关的复杂度,或许是 O(logn)?因为既然是有序,那么很自然地会联想到二分法。考虑外层循环嵌套二分法,那么复杂度应该是 O(n logn)
〖大致流程?〗
- 由于数组是有序的,且考虑二分法,那么:首先和 mid 比较,若
target > nums[mid],那么数组后半部分全部都比 target 大,相加的结果不可能是 target,就把搜索范围缩到数组左半部分;反之,搜索数组右半部分 - 用 2 个指针
begin和end标识搜索范围
- 〖什么时候停?〗
- 当头指针不再位于尾指针之前时,停止
〖特别注意?〗
+ 答案要求的是「顺序」而非「下标」(顺序 = 下标 + 1)〖能否剪枝?〗暂时看不出剪枝的可能
【代码】
class Solution(object):
def twoSum(self, numbers, target):
"""
:type numbers: List[int]
:type target: int
:rtype: List[int]
"""
lenOfNums = len(numbers)
for ind in range(lenOfNums-1):
# two pointers
indices_base1 = [ind+1]
begin = ind+1
end = lenOfNums-1
newTarget = target-numbers[ind]
#print newTarget
# use binary search
while (begin < end):
mid = begin + (end-begin)/2
#print "(before if) begin: {}, end: {}, mid: {}".format(begin, end, mid)
if (0 == newTarget - numbers[mid]):
indices_base1.append(mid+1)
break
elif (newTarget > numbers[mid]):
begin = mid + 1
else:
end = mid - 1
#print "(after if) begin: {}, end: {}, mid: {}".format(begin, end, mid)
if 2 == len(indices_base1):
return indices_base1
elif (0 == newTarget - numbers[begin]):
return [ind+1, begin+1]
elif (0 == newTarget - numbers[end] and end != ind):
return [ind+1, end+1]
else:
continue
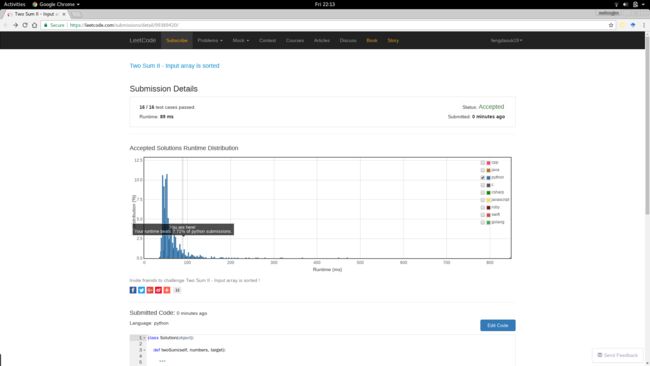
【结果】
运行时:89 ms
报告链接:https://leetcode.com/submissions/detail/99389420/
不知道其他拥有 LeetCode 帐号的人能不能看到该报告,所以顺便附图如下:
看样子还是用之前的哈系法写看看吧,至少复杂度只有 O(n)……
02
【语言】
Python
【时间】
170407
【思路】
- 可以用一个字典(HashMap) dict 来存储这样的键值对:主键是 target-num,键值是数组中能与 target-num 配对组合成 target 的数即 num 的下标 ind(如果有这样的数的话)
- 在遍历数组时,每遇到一个新的数 num,就去字典中找看看是否存在 dict[num],若不存在,说明在 num 之前没有遇到能与当前 num 配对的数 target-num 等待配对,那么就创建新的「键-值」映射;若存在,说明之前已经有一个 target-num 在等待配对,因此找到了答案,直接输出即可
【代码】
class Solution(object):
def twoSum(self, numbers, target):
"""
:type numbers: List[int]
:type target: int
:rtype: List[int]
"""
lenOfNums = len(numbers)
pair = {}
for ind in range(lenOfNums):
if numbers[ind] not in pair:
pair[target - numbers[ind]] = ind
else:
return [pair[numbers[ind]], ind]
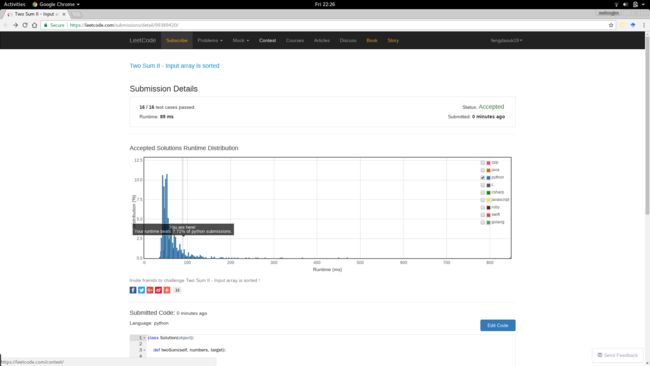
【结果】
运行时:39 ms
报告链接:https://leetcode.com/submissions/detail/99389420/
不知道其他拥有 LeetCode 帐号的人能不能看到该报告,所以顺便附图如下:
不过这个算法并没有利用上「有序(sorted)」的特性
03
【语言】
Python
【时间】
170408
【思路】
考虑下面这张简图
[BEGIN] [END]
|-----|-----|----------|-----|-----|
i a b j
由于有且仅有 1 对数字为答案,这对数字必定在数组首位元素 [BEGIN] 与数组末尾元素 [END] 之间;不妨就设 2 根指针,其一为 i,从 [BEGIN] 开始递增;另一为 j,从 [END] 开始递减。通过某种规则逐渐缩小 i 与 j 之间的距离,直到它们分别命中答案对应的两个数字为止。
那么如何递增/递减?令 sum = numbers[i] + numbers[j],我们的目标是找到恰好满足 sum == target 的 [i, j],这就是说,在找到满足该等式的 [i, j] 前,或者和大于 target,或者和小于 target。因此,我们调整 i 与 j 的判断依据就应该是:sum 的大小,与 target 之间的关系——在 sum > target 时如何增减 i, j,在 sum < target 时如何增减 i, j?
假设答案是 [a, b],那么必然有 a >= numbers[0], b <= numbers[lengthOfNumbers];这就意味着,i 或者不动,或者在 sum < target 时增;j 或者不动,或者在 sum > target 时减——这就是我们要的增减规则,算法即如此。
上述规则有问题吗?是否有可能 i 跑到了 a 的右侧(即 i > a),或者 j 跑到了 b 的左侧(即 j < b)?这是不可能的,我们可以简单论证如下:
- 如果最开始是 i 先向右移动,即最开始
sum < target,那么当 i 增大到一定程度时,最大增加到numbers[i] == a时,此时sum == numbers[i] + numbers[j] == a + numbers[j] > a + b == target,此时必然不会再执行sum < target的分支,从而 i 不会再右移;此后,只会执行sum > target的分支,使 j 不断左移,numbers[j]不断减小,直到找到b == number[j],然后算法就结束(假设在 i 找到 a 后,程序进入了分支sum > target后,要回到sum < target的分支,就必然要经过sum == target这个阶段,因为在 i 再次移动之前,numbers[i] + numbers[j] == a + numbers[j],而 numbers[j] 逐渐减小,要使sum < target,就必须 j 先经过比 b 大的最小数、再经过 b、最后到达比 b 小的最大数,才会再次回到sum < target,否则就与题设「数组中元素升序排列」、「有且仅有一个答案(即一对 [a, b] 满足a + b == target)」矛盾;然而只要考虑到这个过程,就明白算法一定会在回到sum < target前就结束了) - 如果开始时是 j 先向左移动,即最开始
sum > target,那么当 j 减小到一定程度,最小减小到numbers[j] == b时,此时sum == numbers[i] + numbers[j] == numbers[i] + b < a + b == target,此时必然不会再执行sum > target的分支,从而 j 不会再左移;此后,只会执行sum < target的分支,使 i 不断右移,numbers[i]不断增大,直到找到a == numbers[i],然后算法就结束(假设在 j 找到 b 后,程序进入了分支sum < target后,要回到sum > target的分支,就必须 i 先经过比 a 小的最大数、再经过 a、最后到达比 a 大的最小数,才会再次回到sum > target,否则就与题设「数组中元素升序排列」、「有且仅有一个答案(即一对 [a, b] 满足a + b == target)」矛盾;然而只要考虑到这个过程,就明白算法一定会在回到sum > target前就结束了) - 无论算法是 i 先不断递增到 a、然后 j 再不断递减到 b,还是 j 先不断递减到 b、然后 i 再不断递增到 a,或者是两者交替进行——一定会有某一个指针先找到答案配对中的一个数,然后另一个指针的移动情况就必然落到上述 1、2 的情况之一之中
论证完毕。从而代码很简单,见下。
【代码】
class Solution(object):
def twoSum(self, numbers, target):
"""
:type numbers: List[int]
:type target: int
:rtype: List[int]
"""
i = 0
j = len(numbers) - 1
while (numbers[i] + numbers[j] != target):
if (numbers[i] + numbers[j] > target):
j = j - 1
else:
i = i + 1
return [i+1, j+1]
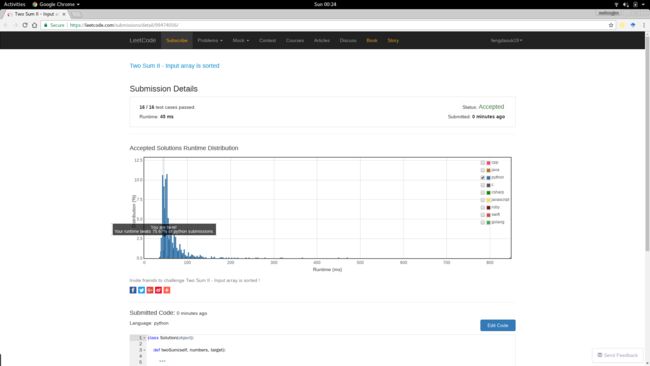
【结果】
运行时:45 ms
报告链接:https://leetcode.com/submissions/detail/99474056/
不知道其他拥有 LeetCode 帐号的人能不能看到该报告,所以顺便附图如下:
这个算法用上了有序的特性,也符合本题在 LeetCode 上的 tag 即「两根指针」。看起来还是之前那个 HashMap 的算法速度快一点,不过毕竟复杂度都是 O(n),因此或许这个差别无伤大雅吧。
03
【语言】
Python
【时间】
170408
【思路】
考虑下面这张简图
[BEGIN] [END]
|-----|-----|----------|-----|-----|
i a b j
由于有且仅有 1 对数字为答案,这对数字必定在数组首位元素 [BEGIN] 与数组末尾元素 [END] 之间;不妨就设 2 根指针,其一为 i,从 [BEGIN] 开始递增;另一为 j,从 [END] 开始递减。通过某种规则逐渐缩小 i 与 j 之间的距离,直到它们分别命中答案对应的两个数字为止。
那么如何递增/递减?令 sum = numbers[i] + numbers[j],我们的目标是找到恰好满足 sum == target 的 [i, j],这就是说,在找到满足该等式的 [i, j] 前,或者和大于 target,或者和小于 target。因此,我们调整 i 与 j 的判断依据就应该是:sum 的大小,与 target 之间的关系——在 sum > target 时如何增减 i, j,在 sum < target 时如何增减 i, j?
假设答案是 [a, b],那么必然有 a >= numbers[0], b <= numbers[lengthOfNumbers];这就意味着,i 或者不动,或者在 sum < target 时增;j 或者不动,或者在 sum > target 时减——这就是我们要的增减规则,算法即如此。
上述规则有问题吗?是否有可能 i 跑到了 a 的右侧(即 i > a),或者 j 跑到了 b 的左侧(即 j < b)?这是不可能的,我们可以简单论证如下:
- 如果最开始是 i 先向右移动,即最开始
sum < target,那么当 i 增大到一定程度时,最大增加到numbers[i] == a时,此时sum == numbers[i] + numbers[j] == a + numbers[j] > a + b == target,此时必然不会再执行sum < target的分支,从而 i 不会再右移;此后,只会执行sum > target的分支,使 j 不断左移,numbers[j]不断减小,直到找到b == number[j],然后算法就结束(假设在 i 找到 a 后,程序进入了分支sum > target后,要回到sum < target的分支,就必然要经过sum == target这个阶段,因为在 i 再次移动之前,numbers[i] + numbers[j] == a + numbers[j],而 numbers[j] 逐渐减小,要使sum < target,就必须 j 先经过比 b 大的最小数、再经过 b、最后到达比 b 小的最大数,才会再次回到sum < target,否则就与题设「数组中元素升序排列」、「有且仅有一个答案(即一对 [a, b] 满足a + b == target)」矛盾;然而只要考虑到这个过程,就明白算法一定会在回到sum < target前就结束了) - 如果开始时是 j 先向左移动,即最开始
sum > target,那么当 j 减小到一定程度,最小减小到numbers[j] == b时,此时sum == numbers[i] + numbers[j] == numbers[i] + b < a + b == target,此时必然不会再执行sum > target的分支,从而 j 不会再左移;此后,只会执行sum < target的分支,使 i 不断右移,numbers[i]不断增大,直到找到a == numbers[i],然后算法就结束(假设在 j 找到 b 后,程序进入了分支sum < target后,要回到sum > target的分支,就必须 i 先经过比 a 小的最大数、再经过 a、最后到达比 a 大的最小数,才会再次回到sum > target,否则就与题设「数组中元素升序排列」、「有且仅有一个答案(即一对 [a, b] 满足a + b == target)」矛盾;然而只要考虑到这个过程,就明白算法一定会在回到sum > target前就结束了) - 无论算法是 i 先不断递增到 a、然后 j 再不断递减到 b,还是 j 先不断递减到 b、然后 i 再不断递增到 a,或者是两者交替进行——一定会有某一个指针先找到答案配对中的一个数,然后另一个指针的移动情况就必然落到上述 1、2 的情况之一之中
论证完毕。从而代码很简单,见下。
【代码】
class Solution(object):
def twoSum(self, numbers, target):
"""
:type numbers: List[int]
:type target: int
:rtype: List[int]
"""
i = 0
j = len(numbers) - 1
while (numbers[i] + numbers[j] != target):
if (numbers[i] + numbers[j] > target):
j = j - 1
else:
i = i + 1
return [i+1, j+1]
【结果】
运行时:45 ms
报告链接:https://leetcode.com/submissions/detail/99474056/
不知道其他拥有 LeetCode 帐号的人能不能看到该报告,所以顺便附图如下:
这个算法用上了有序的特性,也符合本题在 LeetCode 上的 tag 即「两根指针」。看起来还是之前那个 HashMap 的算法速度快一点,不过毕竟复杂度都是 O(n),因此或许这个差别无伤大雅吧。
04
【语言】
C++
【时间】
170409
【思路】
(思路和 01 的思路一致,即为每一个数 num 构造 HashMap,以 target-num 为主键,以 num 为键值,扫描一遍过去,一旦在后面找到这个 target-num 就返回答案。)
【代码】
class Solution {
public:
vector twoSum(vector& numbers, int target) {
std::unordered_map pair;
for (int i=0; i{pair[numbers[i]]+1, i+1};
}
}
}
};
【结果】
运行时:9 ms
报告链接:https://leetcode.com/submissions/detail/99547389/
不知道其他拥有 LeetCode 帐号的人能不能看到该报告,所以顺便附图如下:
呃居然才超过 10.92%……来试看看利用了「升序」特性的 O(n) 解法好了
05
【语言】
C++
【时间】
170409
【思路】
(思路和 03 的思路一致,利用了升序的特性,两根指针逐渐缩小搜索区间)
【代码】
class Solution {
public:
vector twoSum(vector& numbers, int target) {
int i = 0;
int j = numbers.size()-1;
while (numbers[i] + numbers[j] != target)
{
if (numbers[i] + numbers[j] > target)
{
j--;
}
else
{
i++;
}
}
return vector{i+1, j+1};
}
};
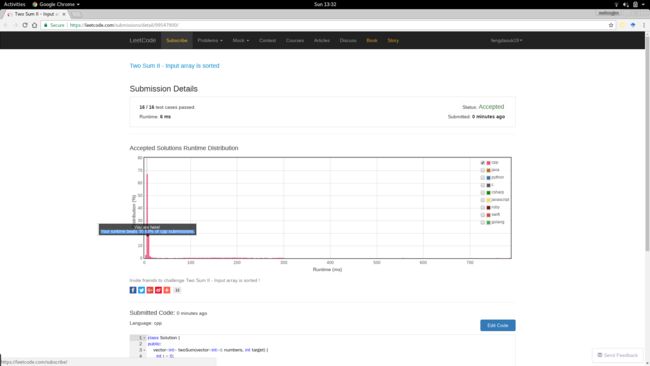
【结果】
运行时:6 ms
报告链接:https://leetcode.com/submissions/detail/99547900/
不知道其他拥有 LeetCode 帐号的人能不能看到该报告,所以顺便附图如下:
啊这个算法在 C++ 中反而比 HashMap 快……
00
自己实现一遍最优解:
- 140409-C++
- 。。。