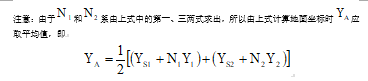一、原理
二、步骤
a.用各自像片的角元素计算出左右像片的旋转矩阵R1和R2。
b.根据左右像片的外方位元素计算摄影基线分量Bx,By,Bz。
c.逐点计算像点的空间辅助坐标。
d.计算投影系数。
e.计算未知点的地面摄影测量坐标。
f.重复以上步骤完成所有点的地面坐标的计算。
三、示例代码
# -*- coding: utf-8 -*- """ Created on Mon Nov 25 08:18:30 2019 @author: L JL """ import numpy as np import math as m def r_mat(f,w,k): Rf = np.mat([[m.cos(f), 0, -m.sin(f)], [0, 1, 0], [m.sin(f), 0, m.cos(f)]]) Rw = np.mat([[1, 0, 0], [0, m.cos(w), -m.sin(w)], [0, m.sin(w), m.cos(w)]]) Rk = np.mat([[m.cos(k), -m.sin(k), 0], [m.sin(k), m.cos(k), 0], [0, 0, 1]]) R = Rf*Rw*Rk return R def SpatialAuxiliaryCoordinate(xy,f,R): coor1 = np.mat([[xy[0]], [xy[1]], [-f]]) coor2 = R*coor1 return coor2 def ProjectionCoefficient(SAC1,SAC2,B): N1 = (B[0,0]*SAC2[2,0]-B[2,0]*SAC2[0,0])/(SAC1[0,0]*SAC2[2,0]-SAC2[0,0]*SAC1[2,0]) N2 = (B[0,0]*SAC1[2,0]-B[2,0]*SAC1[0,0])/(SAC1[0,0]*SAC2[2,0]-SAC2[0,0]*SAC1[2,0]) return N1,N2 #main left_HomonymousImagePoints = [0.153,91.798] right_HomonymousImagePoints = [-78.672,89.122] left_In = np.mat([0,0,152.91]) left_Ex = np.mat([[970302.448784], [-1138644.971216], [3154.584941], [0.010425], [-0.012437], [0.003380]]) right_In = np.mat([0,0,152.91]) right_Ex = np.mat([[971265.303768], [-1138634.245942], [3154.784258], [0.008870], [-0.005062], [-0.008703]]) R_L = np.mat(np.zeros((3,3))) R_R = np.mat(np.zeros((3,3))) left_SACoordinate = np.mat(np.zeros((3,1))) right_SACoordinate = np.mat(np.zeros((3,1))) baselineComponent = np.mat(np.zeros((3,1))) R_L = r_mat(left_Ex[3,0],left_Ex[4,0],left_Ex[5,0]) R_R = r_mat(right_Ex[3,0],right_Ex[4,0],right_Ex[5,0]) #left_SpatialAuxiliaryCoordinate = R_L*left_In.T #right_SpatialAuxiliaryCoordinate = R_R*right_In.T left_SACoordinate = SpatialAuxiliaryCoordinate(left_HomonymousImagePoints,left_In[0,2],R_L) right_SACoordinate = SpatialAuxiliaryCoordinate(right_HomonymousImagePoints,right_In[0,2],R_R) baselineComponent = right_Ex[0:3,0] - left_Ex[0:3,0] N1,N2 = ProjectionCoefficient(left_SACoordinate,right_SACoordinate,baselineComponent) #GPhotogrammetrCoordinates GPCoordinates = np.mat(np.zeros((3,1))) GPCoordinates = ((left_Ex[0:3,0]+N1*left_SACoordinate) + (right_Ex[0:3,0]+N2*right_SACoordinate))/2 print("左影像同名点:",left_HomonymousImagePoints) print("左影像同名点:",right_HomonymousImagePoints) print("地面点坐标:\n X=%f,\n Y=%f,\n Z=%f" %(GPCoordinates[0,0],GPCoordinates[1,0],GPCoordinates[2,0]))