import numpy as np # numpy数值计算,支持维度数组和矩阵计算
# 特殊创建矩阵方式
x = np.zeros((2, 3)) # zeros 创建全是 0 的数组矩阵,参数是数组类型
y = np.ones(3) # ones 创建全是 1 的数组矩阵
z = np.full((3, 2), 3) # full 创建定值数组矩阵,如创建3行2列,数值全是3的矩阵
s = np.eye(5, k=2) # eye 创建对角矩阵,对角值为 1 ,k值表示从第几列开始对角相同,不填默认为 0
w = np.random.random((2, 3)) # 创建随机值的矩阵
# 初始化创建矩阵方式
a = np.array([[1, 2, 3], [3, 4, 5]],dtype=np.int64) # 初始化一个数组成矩阵,dtype= 设置数据类型
print(a.shape) # 查看这个矩阵是几行几列
a1 = a[[1, 0, 1], [0, 1, 1]] # 索引结果是[3,2,4],前后保持一一对应
a2 = [a[1, 0], a[0, 1], a[1, 1]] # 与上面结果相同
rows = np.array([[0, 0], [1, 1]]) # 索引矩阵的行
cols = np.array([[0, 1], [0, 1]]) # 索引矩阵的列
print(a[rows, cols]) # 索引到矩阵的对角值,索引行,列一一对应:[0,0],[0,1],[1,0],[1,1]
print(a > 2) # 判断矩阵中每个元素是否大于2,返回的是布尔值
print(np.sum(a)) # 矩阵中每个元素的求和
print(np.sum(a, axis=0)) # axis = 0 矩阵第一维度求和,[1+3, 2+4, 3+5]
print(np.sum(a, axis=1)) # axis = 1 矩阵第二维度求和,[1+2+3, 3+4+5]
"""
这是二维数组,所以axis=1时就到了最后的维度,将数组最小单位元素相加就可
如是三维数组[[[1,2,3],[3,4,5]],[[6,7,8],[8,9,10]]]
axis=0时求和:[[1+6,2+7,3+8],[3+8,4+9,5+10]]
axis=1时求和:[[1+3,2+4,3+5],[6+8,7+9,8+10]]
axis=2时求和:[[1+2+3,3+4+5],[6+7+8,8+9+10]]
以此类推,数组中每个维度的元素对应元素求和
本质是数组中每个元素相加,
如这个三维数组有两个元素,分别为[[1,2,3],[3,4,5]] 和 [[6,7,8],[8,9,10]]]对应相加,
每个元素中又有两个子元素,分别为[1,2,3] 和 [3,4,5]每个元素中两子元素对应相加,
每个子元素中又有三个子元素,[1,2,3]则这三个子元素相加
"""
"""
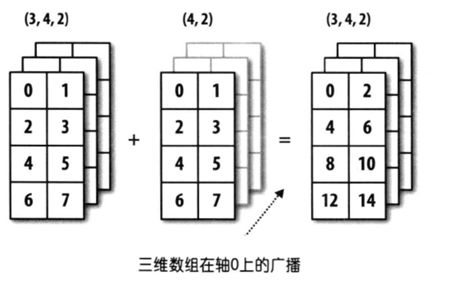
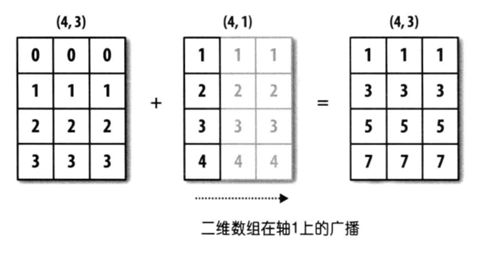
广播(broadcast):是numpy对不同形状(shape)的数组进行数值计算
当两个数组的shape相同,即a.shape==b.shape时,a*b,就是将对应位相乘
但当两个数组的shape不同,则会触发广播机制,触发后会向最长的轴长看齐,不足的补足
广播机制原则:1、两个数组维度不同,但后缘维度的轴长度相同
2、数组维度相同,但其中一个数组轴长为1
如:a是(3,1)的数组,b是(1,3)的数组,运算得到的数组是(3*3)的数组
a为(3,3)数组,b为(2,3)数组,则不满足广播机制原则,不会触发
"""
数组维度不同,后缘轴长相同
数组维度相同,其中一个轴长为1
迭代,for循环,使用nditer迭代出每个元素
# a = [[1, 2, 3], [3, 4, 5]]
for i in np.nditer(a):
print(i) # 结果是1,2,3,3,4,5
for i in np.nditer(a.T): # .T 行列转置
print(i) # 结果是1,2,3,3,4,5
for i in np.nditer(a.T,order='F'): # order='F'列序排序
print(i) # 结果是1,2,3,3,4,5
for i in np.nditer(a.T.copy(order='C')): # order='C'行序排序
print(i) # 结果是1,3,2,4,3,5
for i in np.nditer(a,op_flags=['readwrite']): # 默认是readonly,使用op_flags设置读写性
i[...] = i * 2
print(a)
广播迭代,如果两个数组可广播,则可以同时迭代他们,迭代按广播后的维度轴长迭代
for i,j in np.nditer([s1,s2]):
print('%d:%d' % (i, j))
外部迭代
"""
nditer拥有flags参数,可接受下列值
c_index 按照c顺序迭代
f_index 按照Fortran顺序
multi_index 每次迭代可以跟踪一种索引类型
external_loop 以一维数组形式迭代
"""
for i in np.nditer(a,flags=['external_loop'],order='F'):
print(i)