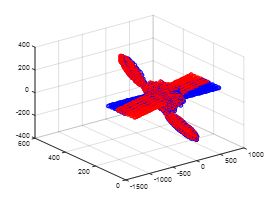
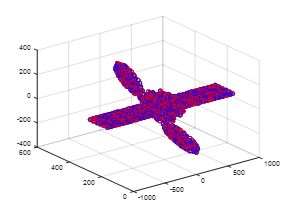
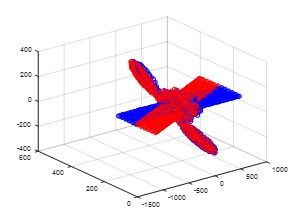
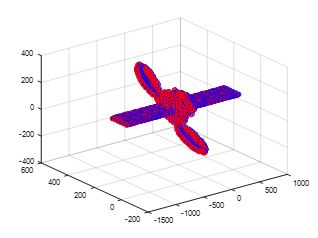
ICP算法主要用于点云精配准,精度很高,但是相应的缺点就是迭代过程中容易陷入局部极值。具体的ICP算法推导过程很多书上都有,就不再详述了,此次仿真用的是SVD分解的方法。
直接贴代码:
clear;
close all;
clc;
data_source=load('satellite.txt');
data_source=data_source';
theta=4; %旋转角度(此处只有绕z轴旋转)
t=[2,1.6,7]; %平移向量
[data_target,T0]=rotate(data_source,theta,t);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%绘制两幅原始图像
x1=data_source(1,:);
y1=data_source(2,:);
z1=data_source(3,:);
x2=data_target(1,:);
y2=data_target(2,:);
z2=data_target(3,:);
figure;
scatter3(x1,y1,z1,'b');
hold on;
scatter3(x2,y2,z2,'r');
hold off;
T_final=eye(4,4); %旋转矩阵初始值
iteration=0;
Rf=T_final(1:3,1:3);
Tf=T_final(1:3,4);
data_target=Rf*data_target+Tf*ones(1,size(data_target,2)); %初次更新点集(代表粗配准结果)
err=1;
while(err>0.001)
iteration=iteration+1; %迭代次数
disp(['迭代次数ieration=',num2str(iteration)]);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%利用欧式距离找出对应点集
k=size(data_target,2);
for i = 1:k
data_q1(1,:) = data_source(1,:) - data_target(1,i); % 两个点集中的点x坐标之差
data_q1(2,:) = data_source(2,:) - data_target(2,i); % 两个点集中的点y坐标之差
data_q1(3,:) = data_source(3,:) - data_target(3,i); % 两个点集中的点z坐标之差
distance = data_q1(1,:).^2 + data_q1(2,:).^2 + data_q1(3,:).^2; % 欧氏距离
[min_dis, min_index] = min(distance); % 找到距离最小的那个点
data_mid(:,i) = data_source(:,min_index); % 将那个点保存为对应点
error(i) = min_dis; % 保存距离差值
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%去中心化
data_target_mean=mean(data_target,2);
data_mid_mean=mean(data_mid,2);
data_target_c=data_target-data_target_mean*ones(1,size(data_target,2));
data_mid_c=data_mid-data_mid_mean*ones(1,size(data_mid,2));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%SVD分解
W=zeros(3,3);
for j=1:size(data_target_c,2)
W=W+data_mid_c(:,j)*data_target_c(:,j)';
end
[U,S,V]=svd(W);
Rf=U*V';
Tf=data_mid_mean-Rf*data_target_mean;
err=mean(error);
T_t=[Rf,Tf];
T_t=[T_t;0,0,0,1];
T_final=T_t*T_final; %更新旋转矩阵
disp(['误差err=',num2str(err)]);
disp('旋转矩阵T=');
disp(T_final);
data_target=Rf*data_target+Tf*ones(1,size(data_target,2)); %更新点集
if iteration>=200
break
end
end
disp(inv(T0)); %旋转矩阵真值
x1=data_source(1,:);
y1=data_source(2,:);
z1=data_source(3,:);
x2=data_target(1,:);
y2=data_target(2,:);
z2=data_target(3,:);
figure;
scatter3(x1,y1,z1,'b');
hold on;
scatter3(x2,y2,z2,'r');
hold off;
rotate.m
function [data_q,T] = rotate(data,theta,t)
theta=-theta/180*pi;
T=[cos(theta),sin(theta),0,t(1);
-sin(theta),cos(theta),0,t(2);
0,0,1,t(3);
0,0,0,1]; %旋转矩阵
rows=size(data,2);
rows_one=ones(1,rows);
data=[data;rows_one]; %化为齐次坐标
data_q=T*data;
data_q=data_q(1:3,:); %返回三维坐标
仿真结果(配准前和配准后):
旋转矩阵(真值和配准结果)
误差:err=0.00019434
注:关于误差的定义每个人可以不同,此处不用太过于计较
上面是比较好的配准结果,下面来一组局部极值的情况。
仿真结果(配准前和配准后):
旋转矩阵(真值和配准结果)
结论: 从上面两组仿真结果可以明显看到,ICP算法在一定情况下精度很高,很适合用来精配准,但是缺点在于需要很好的迭代初值,这个直接关系到配准结果的准确性,因此ICP最好不要单独使用,应该在该算法之前进行粗配准(该方法很多,比如利用特征点等)。另外,由于不知道两堆点云的点对对应关系,在此使用的是寻找最近点的方法,该方法最大的不足时运算量很大,因此如果在C++中使用,可以考虑采用KD-tree的存储方法提高搜索效率或者想办法进行高效率点云配对。