逐行递推的动态规划

逐行递推

---

逐行递推：\(dp\)在某种情况下按照一行一行的顺序进行递推。

P2704 [NOI2001]炮兵阵地

题目描述

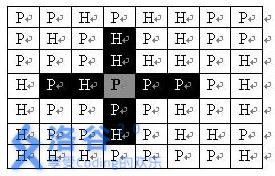
司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。一个N*M的地图由N行M列组成，地图的每一格可能是山地（用“H” 表示），也可能是平原（用“P”表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入输出格式

输入格式：

第一行包含两个由空格分割开的正整数，分别表示N和M；

接下来的N行，每一行含有连续的M个字符（‘P’或者‘H’），中间没有空格。按顺序表示地图中每一行的数据。N≤100；M≤10。

输出格式：

仅一行，包含一个整数K，表示最多能摆放的炮兵部队的数量。

输入样例#1： 复制

5 4
PHPP
PPHH
PPPP
PHPP
PHHP

输出样例#1： 复制

6

题解

这里可以采用逐行递推的方式：定义
\[ f(i,s,t) = \max_{0 ≤ r < 2^m, ~s \&r =0,~t\&r = 0,~s\&t=0,~(r>>1)\&r=0,~(r>>2) = 0, map[i]\&r=0}\{f(i+1, r,s) + count[r]\} \]
其中，\(f(i,s,t)\)表示在第\(i\)行，其前一行的炮兵安排表示为\(s\)，再前一行的炮兵安排表示为\(t\)的时候的放炮数量（从第\(n\)行向第\(1\)行转移，其中\(r\)表示当前这一行的炮兵按放）。由于每一格上，炮兵只能放或者不放，所以可以表示为一个二进制数。

下面，解释\(\max\)的条件：

1. \(0 ≤ r < 2^m\)：穷举所有的当前行的炮兵按放可能性
2. \(s ~\& ~r = 0\)：当这一行与上一行没有一列是重复的情况下（取与的操作可以达到这一目的）
3. \(t~\&~r = 0\)：当这一行与上上行没有一列是重复的情况下
4. \(s~\&~t = 0\)：当上一行与上上行没有一列是重复的情况下
5. \((r >> 1)~\&~r = 0\)：这一行任意一个炮的相邻位置没炮（位移一位就是相邻）
6. \((r >> 2)~\& ~r = 0\)：这一行任意一个炮的相邻\(2\)格位置没炮（位移两位就是相邻\(2\)格）
7. \(map[i] ~\&~r = 0\)：这一行的炮兵安排要与地形匹配

\(count[r]\)：表示\(r\)这样的安排会有多少门炮（由于是二进制，换言之就是有几个一）。

由于数组会太大，所以需要==滚动数组==。

AC代码：

#include 
#include 

using namespace std;

const int maxn = 1030;

int n, m, mp[maxn], cnt[maxn], f[2][maxn][maxn];

vector v;

int main() {
    cin >> n >> m;
    for (int i = 0; i < n; i ++) {
        char c;
        for (int j = 0; j < m; j ++) {
            cin >> c;
            // 将地形储存为二进制
            if (c == 'P') mp[i] = mp[i] * 2;
            else            mp[i] = mp[i] * 2 + 1;
        }
    }

    // 记录一个二进制数含有几个1
    for (int i = 1; i < (1 << m); i ++)
        // cnt[i]存的是作为一个二进制数有几个一
        cnt[i] = cnt[i >> 1] + (i & 1);
        // 记录有效的地形
    for (int r = 0; r < (1 << m); r ++) {
        // 相邻两格不能重复
        if (((r >> 1) & r) == 0)
            // 相邻三个格子只能有一个，所以位移两位再取“与”
            if (((r >> 2) & r) == 0) {
                // 用v记录所有的有效单行布局
                v.push_back(r);
            }
    }

    
    for (int i = n - 1; i >= 0; i --) {
        // 穷举在有效地形内的s
        for (int x = 0; x < v.size(); x ++) {
            int s = v[x];
            // 穷举在有效地形内的t
            for (int y = 0; y < v.size(); y ++) {
                int t = v[y];
                // 当s，t同时可以存在时
                if ((s & t) == 0) {
                    // 穷举这一行的所有地形
                    for (int z = 0; z < v.size(); z ++) {
                        int r = v[z];
                        // 这一行地形不可以与前一行同列
                        if ((r & s) == 0)
                        // 这一行地形不可以与上上行同列
                        if ((r & t) == 0)
                        // 这一地形必须与地图匹配(地形)
                        if ((r & mp[i]) == 0)
                        // 使用滚动数组更新答案(否则MLE会爆)
     f[i % 2][s][t] = max(f[i % 2][s][t], f[(i + 1) % 2][r][s] + cnt[r]);
                    }
                }
            }
        }
    }
    // 答案为穷举第二，第三行所有地形情况下的放炮总数
    int ans = 0;
    for (int i = 0; i < v.size(); i ++) {
        int s = v[i];
        for (int j = 0; j < v.size(); j ++) {
            int t = v[j];
            ans = max(ans, f[0][s][t]);
        }
    }
    cout << ans << endl;
    return 0;
}