Lesson 3 Structuring Machine Learning Projects
这篇文章其实是 Coursera 上吴恩达老师的深度学习专业课程的第三门课程的课程笔记。
参考了其他人的笔记继续归纳的。
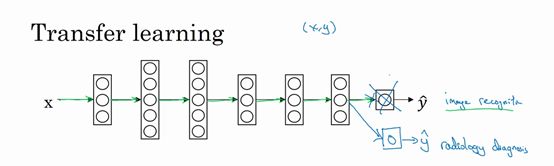
迁移学习 (Transfer learning)
深度学习中,最强大的理念之一就是,有的时候神经网络可以从一个任务中习得知识,并将这些知识应用到另一个独立的任务中。
假如说我们已经训练好一个图像识别神经网络,如猫狗识别器之类的,然后我们让它适应或者说迁移到放射科诊断,类似 X 射线扫描图这种任务。需要做的是,把神经网络最后的输出层删掉以及进入到最后一层的权重删掉,然后为最后一层重新赋予随机权重,让它在放射诊断数据上训练。
经验规则是,如果有一个小数据集,就只训练输出层前的最后一层或两层;但是如果有很多数据,那么也许可以重新训练网络中的所有参数。如果重新训练所有参数的话,在图像识别数据上的初期训练阶段,被称为预训练 (pre-training);而在放射诊断数据上训练的过程,被称为微调 (fine tuning)。
为什么迁移学习会有效果呢?有很多低层次特征,比如说边缘检测、曲线检测、阳性对象检测 (positive objects),从非常大的图形识别数据库中习得这些能力可能有助于我们的学习算法在放射诊断中做得更好。算法学到了很多结构信息,图像形状信息,其中一些知识可能会很有用。
多任务学习 (Multi-task learning)
在迁移学习中,步骤是串行的,从任务 A 里学习只是然后迁移到任务 B。在多任务学习中,任务是同时开始学习的,试图让单个神经网络同时做几件事情,然后希望每个任务都能帮到其他所有任务。
以下面这个例子来说明。
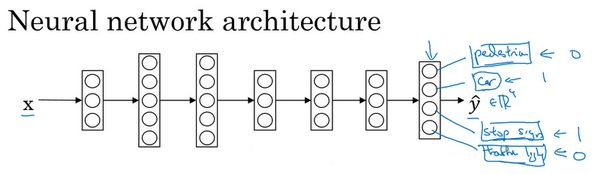
假设我们在研发无人驾驶车辆,那么需要同时检测不同的物体,比如行人、车辆、停车标志以及交通灯等。
上图中输入的图像是 \(x^{(i)}\),对应的标签 \(y^{(i)}\) 不再是一个数值,而是一个向量。假设,现在我们就检测 4 个类别,那么 \(y^{(i)}\) 就是一个 \(4\times1\) 的向量。那么现在我们训练一个神经网络,输入 \(x\),输出是一个四维向量 \(\hat{y}\)。
对于这个神经网络的代价函数如下
\[ J(W^{[1]},b^{[1]},\dots)=\frac{1}{m}\sum^m_{i=1}\sum^4_{j=1}L(\hat{y}_j^{(i)},y_j^{(i)}) \]
其中 \(\sum^4_{j=1}L(\hat{y}_j^{(i)},y_j^{(i)})\) 是单个样本的损失函数,也就是对四个分量的求和。
\[ L(\hat y_{j}^{(i)},y_{j}^{(i)}) = - y_{j}^{(i)}\log\hat y_{j}^{(i)} - (1 - y_{j}^{(i)})log(1 - \hat y_{j}^{(i)}) \]
如果训练的一组任务可以共用低层次特征时,多任务学习可以提供一种有效的方式。
References
[1] Coursera深度学习教程中文笔记
[2] 深度学习 500 问