再给出q个询问,每个询问由非负整数m, k, s组成,问是否能够选出某些物品使得:
- 对于每个选的物品i,满足a[i]<=m且b[i]>m+s。
- 所有选出物品的c[i]的和正好是k。
输入输出样例
输入 #1
5
6 2 7
5 4 9
1 2 4
2 5 8
1 3 9
5
2 7 1
2 7 2
3 2 0
5 7 2
4 1 5
输出 #1
TAK
NIE
TAK
TAK
NIE
正解
将物品按照 a 排序 , 询问按照 m 排序。
这样按顺序枚举询问 , 不断添加物品。之后检查是否合法。
怎么检查呢? 设 f[k] 表示凑到k这个体积 , 所用的b的最小值 , 不断取最小值的最大值 , 进行更新即可 。
考试时只拿了40分的暴力 , 完全没有想到正解。。。
#include
#include
#include
using namespace std;
const int LIM = 1<<19;
char buf[1<<20] , *f1 = buf , *f2 = buf , pbuf[1<<20] , *f3 = pbuf , sta[1<<5];
#define gc() ((f1 == f2 && (f2 = (f1 = buf) + fread(buf , 1 , sizeof buf , stdin) , f1 == f2)) ? EOF : *f1++)
#define Over() fwrite(pbuf , 1 , f3 - pbuf , stdout)
inline int read()
{
register int x = 0; register char c = gc();
while(c < '0' || c > '9') c = gc();
while(c >= '0' && c <= '9') x = (x << 3) + (x << 1) + (c ^ 48) , c = gc();
return x;
}
inline void Pint(int x)
{
if(f3 - pbuf > LIM) Over();
if(!x) { *f3 ++ = '0' , *f3++ = '\n'; return ; }
if(x < 0) *f3 ++ = '-' , x = -x;
char *top = sta;
while(x) { *top ++ = x % 10 + 48 , x /= 10; }
while(top != sta) *f3++ = *--top;
*f3++ = '\n'; return ;
}
const int N = 1100;
int n , Q;
int ail[N*100] , ans[N*N];
struct node { int c , a , b; } w[N];
struct opt{ int m , k , s , id; } r[N*N];
inline bool cmp1(const node &A , const node &B) { return A.a < B.a; }
inline bool cmp2(const opt &A , const opt &B) { return A.m < B.m; }
int main()
{
freopen("a.in" , "r" , stdin);
freopen("a.out" , "w", stdout);
n = read();
for(int i = 1 ; i <= n ; ++i) w[i].c = read() , w[i].a = read() , w[i].b = read();
Q = read();
for(int i = 1 ; i <= Q ; ++i) r[i].m = read() , r[i].k = read() , r[i].s = read() , r[i].id = i;
sort(w + 1 , w + 1 + n , cmp1); sort(r + 1 , r + 1 + Q , cmp2);
ail[0] = 1e9;
for(int i = 1 , j = 1 ; i <= Q ; ++i)
{
while(j <= n && w[j].a <= r[i].m)
{
for(int k = 100000 ; k >= w[j].c ; --k)
ail[k] = max(ail[k] , min(ail[k-w[j].c] , w[j].b));
j++;
}
if(ail[r[i].k] > r[i].m + r[i].s) ans[r[i].id] = 1;
}
for(int i = 1 ; i <= Q ; ++i) puts(ans[i] ? "TAK" : "NIE");
fclose(stdin); fclose(stdout);
return 0;
}
T2 P1848 [USACO12OPEN]书架Bookshelf
当农夫约翰闲的没事干的时候,他喜欢坐下来看书。多年过去,他已经收集了 N 本书 (1 <= N <= 100,000), 他想造一个新的书架来装所有书。
每本书 i 都有宽度 W(i) 和高度 H(i)。书需要按顺序添加到一组书架上;比如说,第一层架子应该包含书籍1 ... k,第二层架子应该以第k + 1本书开始,以下如此。每层架子的总宽度最大为L(1≤L≤1,000,000,000)。每层的高度等于该层上最高的书的高度,并且整个书架的高度是所有层的高度的总和,因为它们都垂直堆叠。
请帮助农夫约翰计算整个书架的最小可能高度。
有N(1 <= N <= 100000)本书,每本书有一个宽度W(i),高度H(i),(1 <= H(i) <= 1,000,000; 1 <= W(i) <= L)。
现在有足够多的书架,书架宽度最多是L (1 <= L <= 1,000,000,000),把书按顺序(先放1,再放2.....)放入书架。某个书架的高度是该书架中所放的最高的书的高度。
将所有书放入书架后,求所有书架的高度和的最小值?
输入格式
第一行:两个数N和L
接下来N行每行两个数Hi和Wi
输出格式
一个数,书架高度的最小值
输入输出样例
输入 #1
5 10
5 7
9 2
8 5
13 2
3 8
输出 #1
21
正解
首先单调栈处理出 i 这个位置之前第一个比他大的位置 , 记为 pre , 那么 pre+1 , i 这段区间内的最大值就是 hi
用线段树维护所有数到 i 的最大的 h 以及这个点的dp值 , 具体的只用维护两个东西 ,
一个是 f 也就是这个点的dp值
另一个是 f+maxh 。然后就没了 。
考试时还算是中规中矩吧 , 但是暴力分也没有拿到满分。。。
改题时 , 居然没有建树赋初值。。。。。。。。。。。。
#include
#include
using namespace std;
const int N = 101000;
const long long inf = 1e18;
char buf[1<<20] , *f1 = buf , *f2 = buf;
#define gc() (f1 == f2 && (f2 = (f1 = buf) + fread(buf , 1 , sizeof buf , stdin) , f1 == f2) ? EOF : *f1++)
inline long long read()
{
register long long x = 0; register char c = gc();
while(c < '0' || c > '9') c = gc();
while(c >= '0' && c <= '9') x = (x << 3) + (x << 1) + (c ^ 48) , c = gc();
return x;
}
int n , L , top;
int pre[N] , sta[N];
long long sum[N] , h[N] , w[N] , tr[N<<2] , f[N<<2] , tag[N<<2] , dp[N];
#define lson k<<1 , l , mid
#define rson k<<1|1 , mid+1 , r
inline void update(int k)
{
f[k] = min(f[k<<1] , f[k<<1|1]);
tr[k] = min(tr[k<<1] , tr[k<<1|1]);
return ;
}
inline void down(int k)
{
if(tag[k] == inf) return ;
tr[k<<1] = f[k<<1] + tag[k];
tr[k<<1|1] = f[k<<1|1] + tag[k];
tag[k<<1] = tag[k<<1|1] = tag[k];
tag[k] = inf; return ;
}
void build(int k , int l , int r)
{
tr[k] = f[k] = tag[k] = inf;
if(l == r) return ; int mid = (l + r) >> 1;
build(lson); build(rson); return ;
}
void Insert(int k , int l , int r , int pos)
{
if(l == r) { f[k] = dp[pos-1]; tr[k] = inf; return ;}
int mid = (l + r) >> 1; down(k);
return (void)(pos <= mid ? Insert(lson , pos) : Insert(rson , pos));
}
void Change(int k , int l , int r , int x , int y , int val)
{
if(x <= l && r <= y) { tr[k] = f[k] + val; tag[k] = val; return ;}
int mid = (l + r) >> 1; down(k);
if(x <= mid) Change(lson , x , y , val);
if(y > mid) Change(rson , x , y , val);
update(k); return ;
}
long long Ask(int k , int l , int r , int x , int y)
{
if(x <= l && r <= y) return tr[k];
int mid = (l + r) >> 1; down(k);
long long ans = inf;
if(x <= mid) ans = min(ans , Ask(lson , x , y));
if(y > mid) ans = min(ans , Ask(rson , x , y));
return ans;
}
int main()
{
// freopen("b.in" , "r" , stdin);
// freopen("b.out" , "w" , stdout);
n = read(); L = read();
for(int i = 1 ; i <= n ; ++i) h[i] = read() , w[i] = read() , sum[i] = sum[i-1] + w[i];
for(int i = n ; i >= 1 ; --i)
{
while(top && h[sta[top]] < h[i]) pre[sta[top--]] = i;
sta[++top] = i;
}
build(1 , 1 , n);
for(int i = 1 ; i <= n ; ++i)
{
Insert(1 , 1 , n , i);
Change(1 , 1 , n , pre[i] + 1 , i , h[i]);
int pos = lower_bound(sum , sum + 1 + i , sum[i] - L) - sum;
if(pos < i) dp[i] = Ask(1 , 1 , n , pos+1 , i);
}
printf("%lld\n" , dp[n]);
fclose(stdin); fclose(stdout);
return 0;
}
T3 P3302 [SDOI2013]森林
题目描述
小Z有一片森林,含有N个节点,每个节点上都有一个非负整数作为权值。初始的时候,森林中有M条边。
小Z希望执行T个操作,操作有两类:
Q x y k查询点x到点y路径上所有的权值中,第k小的权值是多少。此操作保证点x和点y连通,同时这两个节点的路径上至少有k个点。L x y在点x和点y之间连接一条边。保证完成此操作后,仍然是一片森林。
为了体现程序的在线性,我们把输入数据进行了加密。设lastans为程序上一次输出的结果,初始的时候lastans为0。
- 对于一个输入的操作
Q x y k,其真实操作为Q x^lastans y^lastans k^lastans。
- 对于一个输入的操作
L x y,其真实操作为L x^lastans y^lastans。其中^运算符表示异或,等价于pascal中的xor运算符。
请写一个程序來帮助小Z完成这些操作。
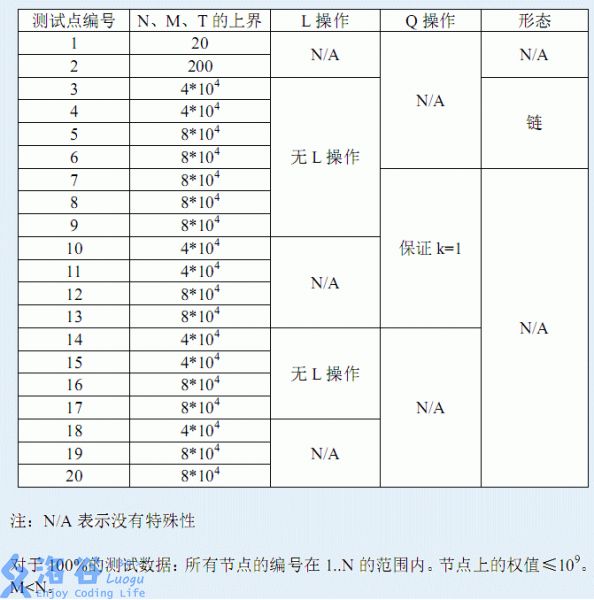
对于所有的数据,\(n,m,T<=8∗10^4\)
输入格式
第一行包含一个正整数testcase,表示当前测试数据的测试点编号。保证1<=testcase<=20。
第二行包含三个整数N,M,T,分别表示节点数、初始边数、操作数。
第三行包含N个非负整数表示 N个节点上的权值。
接下来 M行,每行包含两个整数x和 y,表示初始的时候,点x和点y 之间有一条无向边。
接下来 T行,每行描述一个操作,格式为”Q x y k“或者”L x y “,其含义见题目描述部分。
输出格式
对于每一个第一类操作,输出一个非负整数表示答案。
输入输出样例
输入 #1
1
8 4 8
1 1 2 2 3 3 4 4
4 7
1 8
2 4
2 1
Q 8 7 3 Q 3 5 1
Q 10 0 0
L 5 4
L 3 2 L 0 7
Q 9 2 5 Q 6 1 6
输出 #1
2
2
1
4
2
说明/提示
对于第一个操作 Q 8 7 3,此时 lastans=0,所以真实操作为Q 8^0 7^0 3^0,也即Q 8 7 3。点8到点7的路径上一共有5个点,其权值为4 1 1 2 4。
这些权值中,第三小的为 2,输出 2,lastans变为2。
对于第二个操作 Q 3 5 1 ,此时lastans=2,所以真实操作为Q 3^2 5^2 1^2 ,也即Q 1 7 3。点1到点7的路径上一共有4个点,其权值为 1 1 2 4 。
这些权值中,第三小的为2,输出2,lastans变为 2。之后的操作类似。
这个既有连边又有第k大 , 又像lct , 又像主席树, 结果就蒙逼了。
但是这个题没有删边操作 , 也就是只用考虑主席树怎么合并就行了, 可以考虑启发式合并 。
这样就能过了。。
但是。。。。。。。
毒瘤的Treaker大神 ,把空间开到了 128 MB , 导致必须回收节点。。。。。
回收节点要注意,只能回收这一条链,不能把他fa的也给回收了。。。
还得记得建新边 , 建新边还得注意先回收再连边(不然就把整个树都回收了)
#include
#include
#include
using namespace std;
const int N = 1e5+10;
inline int read()
{
register int x = 0 , f = 0; register char c = getchar();
while(c < '0' || c > '9') f |= c == '-' , c = getchar();
while(c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0' , c = getchar();
return x;
}
int n , m , Q , cnt , tot , id , top;
int a[N] , b[N] , head[N] , root[N] , fa[N] , son[N] , siz[N*100] , ls[N*100] , rs[N*100] , d[N] , f[N][18] , vis[N] , sta[N*20];
struct edge{ int v , nex; } e[N<<1];
inline void add(int u , int v) { e[++cnt].v = v; e[cnt].nex = head[u]; head[u] = cnt; return ; }
inline int Newnode()
{
int x;
if(top) x = sta[top--]; else x = ++id;
siz[x] = ls[x] = rs[x] = 0; return x;
}
int find(int x) { return x == fa[x] ? x : fa[x] = find(fa[x]); }
void Insert(int &x , int y , int l , int r , int pos)
{
x = Newnode(); siz[x] = siz[y] + 1;
if(l == r) return ;
int mid = (l + r) >> 1;
if(pos <= mid) rs[x] = rs[y] , Insert(ls[x] , ls[y] , l , mid , pos);
else ls[x] = ls[y] , Insert(rs[x] , rs[y] , mid + 1 , r , pos);
return ;
}
int Ask(int x , int y , int px , int py , int l , int r , int k)
{
if(l == r) return b[l];
int si = siz[ls[x]] + siz[ls[y]] - siz[ls[px]] - siz[ls[py]] , mid = (l + r) >> 1;
if(si >= k) return Ask(ls[x] , ls[y] , ls[px] , ls[py] , l , mid , k);
else return Ask(rs[x] , rs[y] , rs[px] , rs[py] , mid+1 , r , k - si);
}
int LCA(int x , int y)
{
if(x == y) return x;
if(d[x] < d[y]) swap(x , y);
for(register int i = 17 ; ~i ; --i) x = (d[f[x][i]] >= d[y]) ? f[x][i] : x;
if(x == y) return x;
for(register int i = 17 ; ~i ; --i) if(f[x][i] ^ f[y][i]) x = f[x][i] , y = f[y][i];
return f[x][0];
}
int Query(int x , int y , int k)
{
int p = LCA(x , y);
return Ask(root[x] , root[y] , root[p] , root[f[p][0]] , 1 , tot , k);
}
void dfs(int x , int Fa , int rt)
{
f[x][0] = Fa; fa[x] = Fa; son[rt]++; d[x] = d[Fa] + 1; vis[x] = 1;
for(int i = 1 ; i <= 17 ; ++i) f[x][i] = f[f[x][i-1]][i-1];
Insert(root[x] , root[Fa] , 1 , tot , a[x]);
for(int i = head[x] , v; i ; i = e[i].nex)
{
v = e[i].v; if(v == Fa) continue;
dfs(v , x , rt);
}
return ;
}
void rec(int &x , int y)
{
if(!x) return ;
if(ls[x] != ls[y]) rec(ls[x] , ls[y]);
if(rs[x] != rs[y]) rec(rs[x] , rs[y]);
sta[++top] = x; x = 0; return ;
}
void Rec(int x , int Fa)
{
for(int i = head[x] , v; i ; i = e[i].nex)
{
v = e[i].v; if(v == Fa) continue;
Rec(v , x);
}
rec(root[x] , root[Fa]);
return ;
}
void solve()
{
n = read(); m = read(); Q = read();
register int i , ans = 0 , x , y , k;
for(i = 1 ; i <= n ; ++i) a[i] = read() , b[i] = a[i] , fa[i] = i;
sort(b + 1 , b + 1 + n); tot = unique(b + 1 , b + 1 + n) - b - 1;
for(i = 1 ; i <= n ; ++i) a[i] = lower_bound(b + 1 , b + 1 + tot , a[i]) - b;
for(i = 1; i <= m ; ++i)
{
x = read(); y = read();
add(x , y); add(y , x);
}
for(i = 1 ; i <= n ; ++i) if(!vis[i]) dfs(i , 0 , i) , fa[i] = i;
char c[5];
for(i = 1; i <= Q ; ++i)
{
scanf("%s" , c);
if(c[0] == 'Q')
{
x = read() ^ ans; y = read() ^ ans; k = read() ^ ans;
printf("%d\n" , ans = Query(x , y , k));
}
else
{
x = read() ^ ans , y = read() ^ ans;
int fx = find(x) , fy = find(y);
if(son[fx] < son[fy]) { swap(fx , fy); swap(x , y); }
Rec(fy , 0); dfs(y , x , fx);
add(x , y); add(y , x);
}
}
return ;
}
int main()
{
// freopen("c.in" , "r" , stdin);
// freopen("std.out" , "w" , stdout);
int T = read();
solve();
fclose(stdin); fclose(stdout);
return 0;
}
/*
2
8 4 8
1 1 2 2 3 3 4 4
4 7
1 8
2 4
2 1
Q 8 7 3
Q 3 5 1
Q 10 0 0
L 5 4
L 3 2
L 0 7
Q 9 2 5
Q 6 1 6
8 4 8
1 1 2 2 3 3 4 4
4 7
1 8
2 4
2 1
Q 8 7 3
Q 3 5 1
Q 10 0 0
L 5 4
L 3 2
L 0 7
Q 9 2 5
Q 6 1 6
*/
