流程
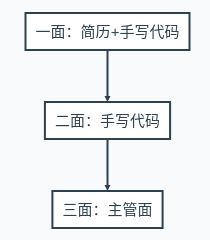
一面全过,二面后开始刷人,如果前两面都是negative,就没有三面。三面后当场可以从HR那里得到大致结果。
一面会根据简历问一些相关问题,都不难,比如机器学习相关的问了聚类和k-means。然后手写代码。二面跟一面差不多,简要介绍以后直接写代码。三面是主管面,内容取决于面试官的性格,可能不写。
代码部分
- 二分搜索返回下标
def BinarySearch(nums, left, right):
if left >= right:
return right
mid = (left +right) //2
#print mid
if nums[mid] < num:
return BinarySearch(nums,mid+1, right)
elif nums[mid] > num:
return BinarySearch(nums, left, mid)
else:
return mid
- 给出二叉树的前序和中序,重建二叉树
def construct_tree(preorder=None, inorder=None):
if not preorder or not inorder:
return None
idx = inorder.index(preorder[0])
left = inorder[:idx]
right = inorder[idx+1:]
root = TreeNode(preorder[0])
root.left = construct_tree(preorder[1:1+len(left)], left)
root.right = construct_tree(preorder[-len(right)], right)
return root
- 快速排序
def quicksort(nums):
if len(nums) < 2:
return nums
pivot = nums[0]
less = [i for i in nums[1:] if i <= pivot]
greater = [i for i in nums[1:] if i > pivot]
return quicksort(less) + [pivot] + quicksort(greater)
- 选择排序
def selectionsort(nums):
for fill in range(len(nums)-1, 0, -1):
maxloc = 0
for loc in range(1, fill+1):
if nums[loc] > nums[maxloc]:
maxloc = loc
nums[fill], nums[maxloc] = nums[maxloc], nums[fill]
return nums
- 希尔排序
step = len(nums) // 2
while step > 0:
for i in range(step, len(nums)):
while i >= step and nums[i] < nums[i - step]:
nums[i], nums[i-step] = nums[i-step], nums[i]
i -= step
step /= 2
return nums
- 堆排序
import numpy as np
def adjust_heap(nums, i):
if 2*i + 1 < len(nums):
children = nums[2*i+1:2*i+3]
n = np.argmax(children)
if max(children) > nums[i]:
if n == 0:
nums[2*i+1], nums[i] = nums[i], nums[2*i+1]
adjust_heap(nums, 2*i+1)
else:
nums[2*i+2], nums[i] = nums[i], nums[2*i+2]
adjust_heap(nums, 2*i+2)
def build_heap(nums):
for i in range((len(nums)-1)//2, -1, -1):
adjust_heap(nums,i)
def heapsort(nums):
i = len(nums) - 1
n = np.argmax(nums)
nums[0], nums[n] = nums[n], nums[0]
build_heap(nums)
while i >= 0:
n = nums.pop(0)
nums.append(n)
num = nums[:i]
adjust_heap(num, 0)
nums[:i] = num
i -= 1
return nums
- $n$根绳子,长度为$l_1-l_n$,剪成$k$段,每段长度相同,怎样使每段的长度最大
这道题与剑指offer中剪绳子的那道颇为相似,但是可以用递归来破解,以下是我的一种解法。
#recursive version
def Divide(nums, k, length):
count = 0
for i in nums:
if i == length:
count += 1
elif i > length:
count += i // length
if count >= k:
return True
return False
def Find(nums, k, length):
if k == 1:
return k, nums[-1]
if length < 1:
return None
if Divide(nums, k, length):
return k, length
else:
return Find(nums, k, length - 1)
#test
nums = [4,3, 2,1]
nums = sorted(nums)
k = 3
sum = sum(nums)
length = sum // k
print Find(nums, k, length)
- 字符串s:
abbacdbab, 字符串p:abb。找s中的字串满足该子串中字母及每个字母对应的个数与p相同,求这样子串的个数
LeetCode 438
class Solution(object):
def findAnagrams(self, s, p):
"""
:type s: str
:type p: str
:rtype: List[int]
"""
res = []
n, m = len(s), len(p)
if n < m: return res
phash, shash = [0]*123, [0]*123
for x in p:
phash[ord(x)] += 1
for x in s[:m-1]:
shash[ord(x)] += 1
for i in range(m-1, n):
shash[ord(s[i])] += 1
if i-m >= 0:
shash[ord(s[i-m])] -= 1
if shash == phash:
res.append(i - m + 1)
return res
- 链表遍历
- 冒泡排序
def bubblesort(nums):
for times in range(len(nums)-1, 0, -1):
for i in range(times):
if nums[i]>nums[i+1]:
nums[i], nums[i+1] = nums[i+1], nums[i]
return nums
- 求给定字符串中包含该字符串所有出现过的字母的最短字串
def ShortestSubstring(str):
if not str:
return None
record = []
count = {}
for s in str:
if s in record:
count[s] += 1
else:
record.append(s)
count[s] = 1
left, right = 0, len(str) - 1
while left <= right:
if count[str[left]] == 1 and count[str[right]] == 1:
return str[left:right+1]
if count[str[left]] > 1:
count[str[left]] -= 1
left += 1
if count[str[left]] == 1 and count[str[right]] > 1:
count[str[right]] -= 1
right -= 1
print ShortestSubstring("abaacdab")
- 非递归版快排
- 插入排序
def insertsort(nums):
for loc in range(1, len(nums)):
currentval = nums[loc]
position = loc
while position > 0 and nums[position-1] > currentval:
nums[position] = nums[position-1]
position -= 1
nums[position] = currentval
return nums
非代码部分
- 判断链表是否有环,如何找出入环点。
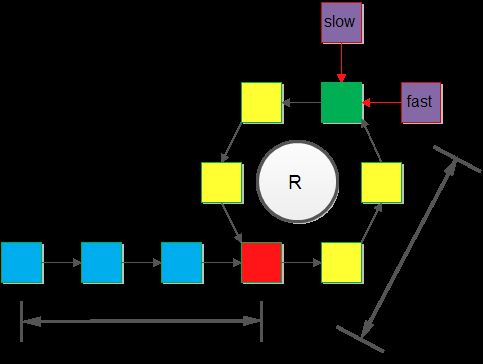
使用快慢指针,初始化为链表头,慢指针每次向后移动1,快指针移动2,遍历链表,如果快慢指针指到同一个位置,说明有环;如果快指针指向了null,说明无环。
假设在第t步快慢指针到达同一个位置,那么此时快指针走了2t,而慢指针走了t。
设环的长度为R,入环点距离链表头距离为len,指针距离入环点为x,快指针共绕环n(n in [1,2, ...])次,那么可以得到等式:
[图片上传失败...(image-466417-1525164880118)]
[图片上传失败...(image-30ea35-1525164880118)]
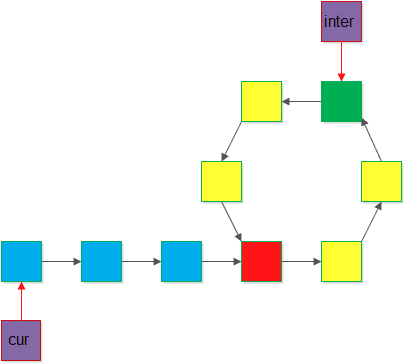
可以证明,n=1,那么len=R-x。
定义一个currnet指针,初始化为链表头,一个inter指针,指向快慢指针的交汇点,两个指针一起向后移动,交汇时即为入环点。
给出一个$n\times n$数值矩阵,从左到右、从上到下依次递增,如何从中快速找到目标值并分析时间复杂度。
从左下角或右上角开始比较,每次可以去掉一行/一列,时间复杂度是O(n)。概率题:10个红球,10个绿球,放入A,B两个箱子中,如何放置才能使随机取一个箱子中的一个球是红球的概率最大。
考虑边界情况的概率最大:A中放10个绿球,9个红球,B中放1个红球,取得红球的概率为
[图片上传失败...(image-21f344-1525164880118)]=0.5(1+\frac{9}{19})=0.74$$)
如何确定是9个红球:
设A中放x个红球则A中取得红球的概率为
[图片上传失败...(image-f33542-1525164880118)]=\frac{x}{10+x},x\in[1,2,\ldots,9]$$)
在定义域上是递增的,因此取9个红球。
欢迎在评论区交流补充