参考资料
chapter3
Maximum margin classifcation with
support vector machines
引言
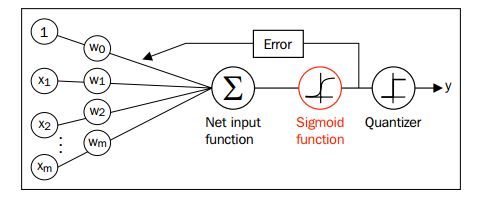
在上一章逻辑回归算法中,我们已经注意到,逻辑回归 LogisticalRegression与线性自适应 Adaline 的区别只在于它们对应的激励函数不同,所以这一章,我们试着自己来构建一个简单的逻辑回归单元
step 1 结构分析
参考感知机单元,我们构建的这个逻辑回归类 应该接受一组训练集,包括一个 nk*的矩阵以及一个n维的列向量 y
这个类应该包括一个求 net_input 的方法来求出 z
一个更新权值并统计损失函数的方法
一个分类器
注意,这个分类器应该以0.5作为阈值
step 2 直接在Adaline的基础上修改代码
# -*- coding: utf-8 -*-
"""
Created on Fri Jun 30 12:57:19 2017
@author: Administrator
"""
import numpy as np
class LogisticalRegression(object):
"""
LogisticalRegression lassifier.
Parameters(参数)
------------
eta : float
Learning rate (between 0.0 and 1.0) 学习效率
n_iter : int
Passes over the training dataset(数据集).
Attributes(属性)
-----------
w_ : 1d-array
Weights after fitting.
errors_ : list
Number of misclassifications in every epoch(时间起点).
"""
def __init__(self, eta=0.01, n_iter=10, C=1.0):
self.eta = eta
self.n_iter = n_iter
self.C = C
def fit(self, X, y):
'''
Fit training data.
Parameters
----------
X : {array-like}, shape = [n_samples, n_features] X的形式是列表的列表
Training vectors, where n_samples is the number of samples
and n_features is the number of features.
y : array-like, shape = [n_samples]
Target values.
Returns
-------
self : object
'''
self.w_ = np.zeros(1 + X.shape[1])
#X.shape = (100,2),zeros 生成的是列向量
#self.w_ 是一个(3,1)的矩阵
# print('X.shape[1]=',X.shape[1])
self.cost_ =[]
#self.cost_损失函数 cost_function
# zeros()创建了一个 长度为 1+X.shape[1] = 1+n_features 的 0数组
# self.w_ 权向量
self.errors_ = []
for i in range(self.n_iter):
output = self.activation(X)
'''
if i==1:
print(output)
print(y)
'''
# y(100,1) output(100,1),errors(100,1)
errors = (y - output)
self.w_[1:] += self.C*self.eta * X.T.dot(errors)
# X先取转置(2,100),再矩阵乘法乘以 errors(100,1) X.T.dot(errors) (2,1)
self.w_[0] += self.C*self.eta * errors.sum()
cost = (errors**2).sum()
self.cost_.append(cost)
'''
ln_output=np.log(output)
cost = y.dot(ln_output)+(1-y).dot(np.log(1-output))
self.cost_.append(cost)
print(self.cost_)
'''
# print(self.w_.shape)
# print(self.w_)
# print(X.shape)
return self
def net_input(self, X):
"""Calculate net input"""
#np.dot(A,B)表示矩阵乘法 ,X(100,2) self.w_[1:](2,1)
#注意 这里每一组 向量x = [x1,x2] 不是 [x1,,,,,,x100]!!!
#所以得到的 net_input 是(100,1)的矩阵 表示100个样本的net_input
return (np.dot(X, self.w_[1:])+self.w_[0])
def activation(self,X):
"""Compute LR activation"""
return 1/(1+np.exp(-self.net_input(X)))
def predict(self, X):
"""return class label after unit step"""
print(self.cost_)
return np.where(self.activation(X)>= 0.5, 1, 0)
同样用 Iris 数据集来测试一下下~
# -*- coding: utf-8 -*-
"""
Created on Fri Jun 30 14:47:25 2017
@author: Administrator
"""
from LR import LogisticalRegression
from sklearn import datasets
from sklearn.cross_validation import train_test_split
from sklearn.preprocessing import StandardScaler
from PDC import plot_decision_regions
import matplotlib.pyplot as plt
import numpy as np
Iris = datasets.load_iris()
x = Iris.data[0:100,2:4]
y = Iris.target[0:100]
X_train,X_test,y_train,y_test = train_test_split(
x,y,test_size=0.3,random_state=0)
sc=StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
Lr=LogisticalRegression(n_iter=20,eta=0.01,C=10)
Lr.fit(X_train_std,y_train)
X_combined_std = np.vstack((X_train_std,X_test_std))
y_combined = np.hstack((y_train,y_test))
plot_decision_regions(X=X_combined_std,y=y_combined,
classifier=Lr,test_idx=range(70,100)
)
'''
plt.scatter(X_test_std[:,0],X_test_std[:,1],c='',edgecolor='0',alpha=1.0,
linewidths=1,marker='o',s=55,label='test')
'''
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='upper left')
plt.savefig('Iris.png')
plt.show()
结果如下
ok!