一些知识
以下内容来自极客时间 -王争-数据结构与算法之美
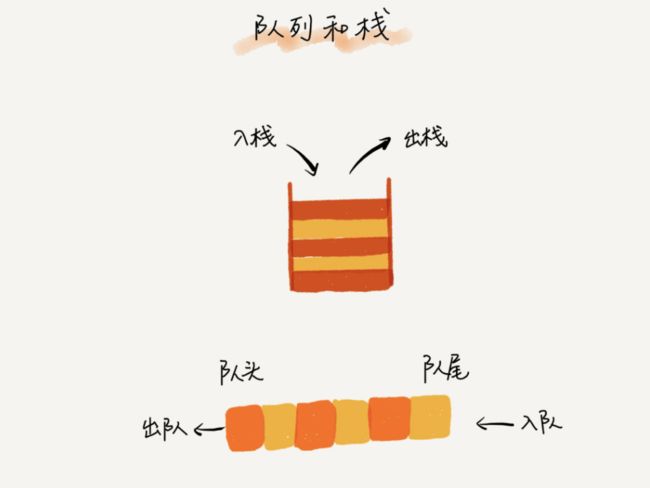
一、什么是队列?
1.先进者先出,这就是典型的“队列”结构。
2.支持两个操作:入队enqueue(),放一个数据到队尾;出队dequeue(),从队头取一个元素。
3.所以,和栈一样,队列也是一种操作受限的线性表。
二、如何实现队列?
1.队列API
public interface Queue
public void enqueue(T item); //入队
public T dequeue(); //出队
public int size(); //统计元素数量
public boolean isNull(); //是否为空
}
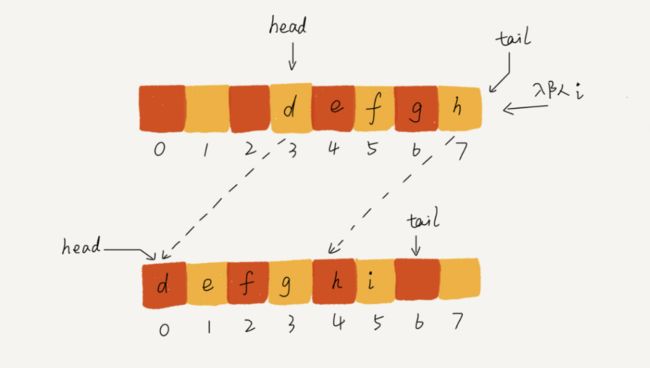
2.数组实现(顺序队列):
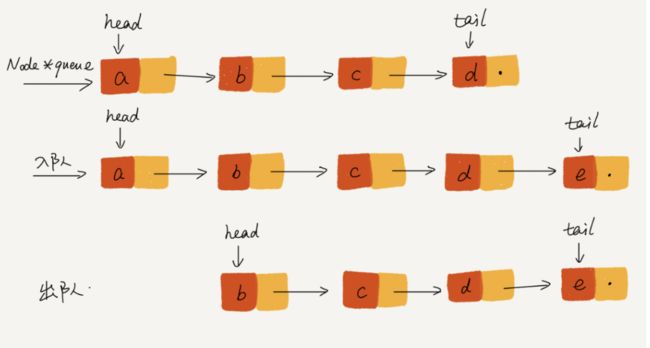
3.链表实现(链式队列):
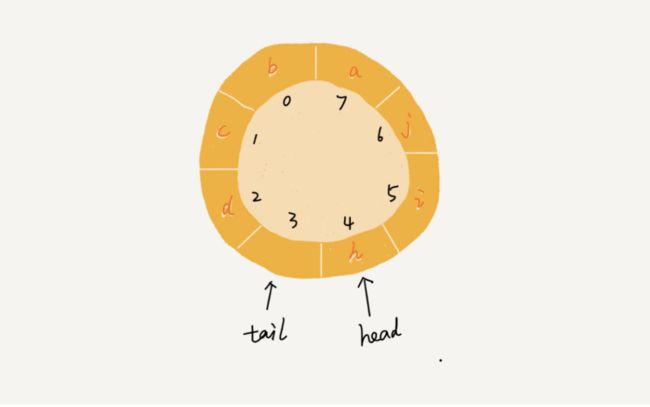
4.循环队列(基于数组):
三、队列有哪些常见的应用?
队列的应用非常广泛,特别是一些具有某些额外特性的队列,比如循环队列、阻塞队列、并发队列。它们在很多偏底层的系统、框架、中间件的开发中,起着关键性的作用。比如高性能队列 Disruptor、Linux 环形缓存,都用到了循环并发队列;Java concurrent 并发包利用 ArrayBlockingQueue 来实现公平锁等。
关于如何实现无锁并发队列
可以使用 cas + 数组的方式实现。
队列的其他应用
分布式消息队列,如 kafka 也是一种队列。
1.阻塞队列
1)在队列的基础上增加阻塞操作,就成了阻塞队列。
2)阻塞队列就是在队列为空的时候,从队头取数据会被阻塞,因为此时还没有数据可取,直到队列中有了数据才能返回;如果队列已经满了,那么插入数据的操作就会被阻塞,直到队列中有空闲位置后再插入数据,然后在返回。
3)从上面的定义可以看出这就是一个“生产者-消费者模型”。这种基于阻塞队列实现的“生产者-消费者模型”可以有效地协调生产和消费的速度。当“生产者”生产数据的速度过快,“消费者”来不及消费时,存储数据的队列很快就会满了,这时生产者就阻塞等待,直到“消费者”消费了数据,“生产者”才会被唤醒继续生产。不仅如此,基于阻塞队列,我们还可以通过协调“生产者”和“消费者”的个数,来提高数据处理效率,比如配置几个消费者,来应对一个生产者。
2.并发队列
1)在多线程的情况下,会有多个线程同时操作队列,这时就会存在线程安全问题。能够有效解决线程安全问题的队列就称为并发队列。
2)并发队列简单的实现就是在enqueue()、dequeue()方法上加锁,但是锁粒度大并发度会比较低,同一时刻仅允许一个存或取操作。
3)实际上,基于数组的循环队列利用CAS原子操作,可以实现非常高效的并发队列。这也是循环队列比链式队列应用更加广泛的原因。
3.线程池资源枯竭是的处理
在资源有限的场景,当没有空闲资源时,基本上都可以通过“队列”这种数据结构来实现请求排队。
四、思考
1.除了线程池这种池结构会用到队列排队请求,还有哪些类似线程池结构或者场景中会用到队列的排队请求呢?
2.今天讲到并发队列,关于如何实现无锁的并发队列,网上有很多讨论。对这个问题,你怎么看?
队列的java语言数组实现
// 用数组实现的队列
public class ArrayQueue {
// 数组:items,数组大小:n
private String[] items;
private int n = 0;
// head表示队头下标,tail表示队尾下标
private int head = 0;
private int tail = 0;
// 申请一个大小为capacity的数组
public ArrayQueue(int capacity) {
items = new String[capacity];
n = capacity;
}
// 入队
public boolean enqueue(String item) {
// 如果tail == n 表示队列已经满了
if (tail == n) return false;
items[tail] = item;
++tail;
return true;
}
// 出队
public String dequeue() {
// 如果head == tail 表示队列为空
if (head == tail) return null;
String ret = items[head];
++head;
return ret;
}
}
数据搬移解决队列满的问题
// 入队操作,将item放入队尾
public boolean enqueue(String item) {
// tail == n表示队列末尾没有空间了
if (tail == n) {
// tail ==n && head==0,表示整个队列都占满了
if (head == 0) return false;
// 数据搬移
for (int i = head; i < tail; ++i) {
items[i-head] = items[i];
}
// 搬移完之后重新更新head和tail
tail -= head;
head = 0;
}
items[tail] = item;
++tail;
return true;
}
基于链表的队列实现
入队时,tail->next= new_node, tail = tail->next;出队时,head = head->next
public class LinkedQueue {
//定义一个节点类
private class Node{
String value;
Node next;
}
//记录队列元素个数
private int size = 0;
//head指向队头结点,tail指向队尾节点
private Node head;
private Node tail;
//申请一个队列
public LinkedQueue(){}
//入队
public boolean enqueue(String item){
Node newNode = new Node();
newNode.value = item;
if (size == 0) head = newNode;
else tail.next = newNode;
tail = newNode;
size++;
return true;
}
//出队
public String dequeue(){
String res = null;
if(size == 0) return res;
if(size == 1) tail = null;
res = head.value;
head = head.next;
size--;
return res;
}
}
循环队列
public class CircularQueue {
// 数组:items,数组大小:n
private String[] items;
private int n = 0;
// head表示队头下标,tail表示队尾下标
private int head = 0;
private int tail = 0;
// 申请一个大小为capacity的数组
public CircularQueue(int capacity) {
items = new String[capacity];
n = capacity;
}
// 入队
public boolean enqueue(String item) {
// 队列满了
if ((tail + 1) % n == head) return false;
items[tail] = item;
tail = (tail + 1) % n;
return true;
}
// 出队
public String dequeue() {
// 如果head == tail 表示队列为空
if (head == tail) return null;
String ret = items[head];
head = (head + 1) % n;
return ret;
}
}
队列的C语言实现
来自https://github.com/TheAlgorithms/C
////////////////////////////////////////////////////////////////////////////////
//INCLUDES
#include
#include
////////////////////////////////////////////////////////////////////////////////
//MACROS: CONSTANTS
////////////////////////////////////////////////////////////////////////////////
//DATA STRUCTURES
struct node {
int data;
struct node* next;
struct node* pre;
} *head, *tail, *tmp;
////////////////////////////////////////////////////////////////////////////////
//GLOBAL VARIABLES
int count;
////////////////////////////////////////////////////////////////////////////////
//FORWARD DECLARATIONS
void create();
void enque(int x);
int deque();
int peek();
int size();
int isEmpty();
////////////////////////////////////////////////////////////////////////////////
//MAIN ENTRY POINT
int main(int argc, char const *argv[]) {
create();
enque(5);
return 0;
}
void create() {
head = NULL;
tail = NULL;
}
/**
* Puts an item into the Queue.
*/
void enque(int x) {
if(head == NULL) {
head = (struct node *)malloc(1 * sizeof(struct node));
head->data = x;
head->pre = NULL;
tail = head;
} else {
tmp = (struct node *)malloc(1 * sizeof(struct node));
tmp->data = x;
tmp->next = tail;
tail = tmp;
}
}
/**
* Takes the next item from the Queue.
*/
int deque() {
int returnData;
if(head == NULL) {
printf("ERROR: Deque from empty queue.\n");
exit(1);
} else {
returnData = head->data;
if(head->pre == NULL)
head = NULL;
else
head = head->pre;
head->next = NULL;
}
}
/**
* Returns the size of the Queue.
*/
int size() {
return count;
}
Reference
图解算法
极客时间 -王争-数据结构与算法之美课程
TheAlgorithms C (C语言代码实现算法)