- 英文地址
- 作者:Martin Ester, Hans-Peter Kriegel, Jiirg Sander, Xiaowei Xu
- 时间:1996
摘要 聚类算法对解决空间数据中的分类问题很有吸引力,然而,大型空间数据对聚类算法产生了下列需求:减少确定输入参数所需要的领域知识,对不规则形状进行聚类以及在大数据上的高效率聚类。目前广为人知的聚类算法无法满足上述需求。本文提出一种新的聚类方法,叫做DBSCAN,是一个基于密度聚类的概念,可以用来解决不规则形状的聚类问题。DBSCAN只需要一个输入参数且支持用户自定义一个合适的值。我们用SEQUIOIA2000基准集的合成数据以及真实数据对DBSCAN的有效性和效率进行了评估。实验结果证明(1)DBSCAN在不规则形状聚类上的表现显著优于著名的CLARANS算法(2)DBSCAN就效率而言超过CLARANS 100倍。
keywords:聚类算法,不规则形状聚类,大型空间数据上的效率,处理噪点
1 Introduction
许多应用需要处理大数据,比如空间数据。Spatial Database Systems(SDBS)(Gueting 1994)是一个管理空间数据的数据集,从卫星图片,X-ray或者其他自动采集一起中获取越来越多的数据。因此,automated knowledge discovery在空间数据中变得越来越重要。
knowledge discovery in databases(KDD)的一些任务在这篇文章中有定义(Matheus,Chan&Piatetsky-Shapiro 1993),这篇文章考虑的任务是class identification,如将数据库中的objects分为有意义的子类,比如在一个地球研究的数据库中,我们可能想找到沿着河流的房屋那类数据。
聚类算法很适合解决这类问题。但是,大型空间数据的应用引发了聚类算法的如下需求:
(1)减少确定输入参数所需要的领域知识,因为在处理大数据的时候,合适的值往往事先不知道。
(2)从不规则形状中发现聚类,因为空间数据聚类的形状可能是球形的,拉长的,线型的或者细长的等等。
(3)在大数据上的效率问题。如在一个数据库上可能有超过一千个物体。
现有聚类算法不足以解决上述问题。本文提出了一个新的聚类算法DBSCAN,只需要一个输入参数并支持用户自定义该参数的值。它可以对不规则形状进行聚类。最后,DBSCAN在大型空间数据中也是可用的。文章的其余部分组织如下:在Section 2讨论了聚类算法,并根据上述需求对它们进行了评估。Section 3提出了我们聚类的概念,是基于数据库的密度概念的。Seciton 4介绍了DBSCAN算法在空间数据上如何发现聚类的。Section 5用SEQUOIA2000基准集上的合成及真实数据进行了实验,评估了有效性以及效率。Section 6 包含总结以及未来研究方向。
2 Clustering Algorithms
有两种基本类型的聚类:partitioning(分区)和hierarchical(分层)算法。Partitioning algorithms构建了一个数据集D的一个分区,将它的n个物体分成k个集合。k是这些算法的输入参数,即一些领域知识是必须的,但是很遗憾,这些知识无法用于许多应用。Partitioning algorithm通常开始于一个初始化的区块D,然后用迭代控制策略优化目标函数,每个类用该类的重力中心表示(k-mean)或者用接近中心的object(k-medoid algorithms)。因此,partitioning algorithms使用连个步骤:首先,决定最小化目标函数的k,然后,将每个对象分配给具有代表性“最近”的集群。第二步意味着分区等同于voronoi图,并且每个簇包含在一个voronoi单元中,因此,通过分区算法找到的所有聚类的形状是凸的,这是非常受限的。
Ng&Han(1994)在空间数据上发现了partitioning algorithms,介绍了CLARANS(Clustering Large Applications based on RANdomized Search),改进了k-medoid方法。和之前的k-medoid算法相比,CLARANS效果更好且更高效,实验评估验证了CLARANS在成千上万个objects的数据库上运行小女更高。Ng&Han(1994)也讨论了在一个数据集上决定knat的方法,他们建议为每个k从2到n运行一次CLARANS。每次运行都会计算一个silhouette系数(Kaufman&Rousseeuw 1990),最后,silhouette系数最大的最接近真实聚类情况。遗憾的是,这个方法的运行时间太久了,O(n)的调用CLARANS。
CLARANS假设所有聚类物体可以都同时放在主存中,不适用于大型数据库。此外,CLARANS在大型数据库上的运行时间是巨大的。因此,Ester,Kriegel&Xu(1995)提出了一些focusing技术,通过将聚类过程focus在与其相关的那部分数据,解决了这两个问题。首先,这个focus足够小,能够放入内存,其次,CLARANS的运行时间和在整个数据集上比起来显著减少。
Hierarchical algorithms(分层算法)创建了D的层次分解。层次分解用一个dendrogram表示,一个树,迭代地把D分解成较小的子集,直到每个子集只包含一个对象。在这样的层次下,每个书借点代表D的一个类。dendrogram可以从叶节点向上到根节点构建,也可以从根节点向下到叶节点构建,构建方式是通过每一步合并或者拆分聚类。和partitioning algorithms不同的是,分层聚类不需要k作为输入。但是,必须指定终止条件,在合并或拆分是作为终止标志。聚类方法终止条件的一个例子是设置Q的每个类的临界距离Dmin。
到目前为止,层次聚类算法的主要问题是很难找到一个合适的终止条件,例如Dmin的值需要足够小,直到能分开所有类,同时又需要足够大,为了没有类被拆分为两个个类。最近,在信号处理领域,层次聚类算法“Ejcluster”被提出,可以自动生成终止条件。它的核心是如果你从一个点走到另一个点只需要“充分小”的一步,则这两个点属于同一类。Ejcluster遵循分裂方法,它不需要任何领域知识。此外,实验证明它在发现非凸聚类中非常有效。可是,Ejcluster因为要对每一对点的距离进行计算所以代价是O(n2)。它被用于很多应用,比如合适的n值的手写识别,但是在大数据上很难应用。
Jain(1988)发现了一种基于密度的对K维点集进行聚类的方法。数据集被划分为很多非重叠cells并构建直方图。高频点数就是潜在的聚类中心,聚类边界就在直方图的“低谷”处。这个方法能对任何形状的分布进行聚类。可是,需要的存储的空间和搜索高维直方图需要的时间是巨大的。尽管对空间和时间进行了优化,但这个方法的表现还是严重依赖于cells的数量。
3 A Density Based Notion of Clusters
看图1绘制的样本点,我们可以很容易看出聚类点以及不属于任何类的噪声点。
我们能识别出类的主要原因是,同一个雷内,能看出明显的高密度点群,比其他类外面的类密度要高。此外,同一区域的噪声密度也比外面低。
后面的部分,我们尽力S空间内的数据集D的k维点集上规范化“cluster”和“noise”的概念。注意,我们的聚类概念和我们的算法DBSCAN,可以应用于2D和3D的欧几里得空间以及高维特征中间中。核心方法是对聚类的每个点,给定半径的邻域必须包含至少一个最小值数目的点。例如,邻域的密度必须超过一些阈值。邻域的形状由两个点p和q的一个距离函数决定,记为dist(p,q)。例如,当使用2D空间中的曼哈顿距离是,聚类的形状会是长方形。注意,为了对给定的应用能提供一个合适的距离函数,我们的方法适用于各种距离函数。为了更好地可视化,所有的用例都以二维空间的欧式距离为例。
定义1:(Eps-neighborhood of a point)一个点p的Eps-neighborhood,用NEps(p)表示,定义为
一种简单的方法是需要聚类的每个点,至少在1个Eps-neighborhood中有MinPts个点。可是这种方法行不通,因为这里有两种点,在类内的点(core points)和在类边界的点(border points)。通常来讲,边界点的Eps-neighborhood区域内的点明显少于core points的Eps-neighborhood的点。因此,为了包含属于同一类的所有点,我们必须将最少点数设置为一个相对较小的值。但是这个值对一些集群来说不是特别相符——尤其是在存在噪声的情况下。因此,我们需要对类C里的每个点p,都有一个点q属于C,使p在q的Eps-neighborhood中,
且N Eps(q)包含至少MinPts个点。这个定义的阐述如下。
定义2: (directly density-reachable直接密度可达)一个点p与点q是直接密度可达,当Eps,MinPts满足:
明显,core points的直接密度可达是对称的。通常来讲,如果一个core point和它的一个边界点的密度可达是不对称的。图2展示了这个情况。
定义3:(density-reachable密度可达) 一个点p与点q是密度可达的,当Eps和MinPts能形成一条链p1,...,pn,p1=q,pn=p,pi+1是pi的直接密度可达。
密度可达是直接密度可达的典型扩展。这中相关性是可传递的,但不是对称的。图3描述了一些样本点,尤其是不对称的情况。尽管通常是不对称的,但是很明显core points的密度可达是对称的。
同一个类C的2个边界点困难彼此不是密度可达的,因为core point condition对它们可能不成立。但是,C中一定有一个core point,从它出发一定更有两个边界点密度可达。因此,我们介绍了密度连通性的概念,它涵盖了边界点的这种关系。
定义4:(density-connected密度连通行)一个点p到点q(with respect to Eps和MinPts)是密度连通的,有一个点o(with respect to Eps和MinPts),从它出发使p和q密度可达。
密度连通性是一种对称关系。对于密度可达的点,密度连通性的关系也是自反的(见图3)。
现在,我们可以定义一个类的基于密度的概念进行定义了。直觉上看,一个类的定义是一系列密度连通的点,拥有最大化的密度可达性。对于给定的类,噪声也随即被定义,即D中不属于任何类的点就是噪声点。
定义5:(cluster)让D为一个点集。一个类C(with respect to Eps 和MinPts)是D的一个非空子集,满足下列条件:
(1)对于所有p,q,如果p输入C,q是p(with respect to Eps&MinPts)的密度可达,则q属于C(Maximality)
(2)对于所有p,q属于C:p是q(with respect to Eps & MinPts)的密度连通点(Connectivity)
定义6:(noise)让C1,...,Ck为D的一系列聚类(with respect to Eps & MinPts),i=1,...,k。然后我们把D中不属于任何聚类Ci的点定义为噪声。
注意,一个类C(with respect to Eps & MinPts)包含至少MinPts个点,因为以下原因:因为C包含至少一个点p,通过一些点o(o可能等于p),p自身一定是密度可达的。因此,至少o能满足core point condition,所以,o的Eps-Neighthood包含至少MinPts个点。
下面点引理对于验证我们的聚类算法非常重要。直观地说,他们陈述了下面这些事:给出参数Eps和MinPts,根据我们方法可以通过两步发现一个聚类。首先,从数据集中选择任意一个满足core point condition的点做种,然后,取出所有从种子点出发密度可达的点,获得聚类的点。
引理1: 定义p为D中的一点,且
然后集合O={o|o属于D,且o从p(with respect to Eps & Minpts)是密度可达的},则O是一个聚类(with respect to Eps & Minpts)。
集群C由任意一个它的core points唯一确定这个特点并不明显。但是,每个C中的点,从任意一个它的core point出发都是密度可达的,因此,一个聚类C包含的点都是从任何一个core point出发都密度可达的点。
引理2:定义C为一个聚类(with respect to Eps&MinPts),p为C中的任意一点,满足
则C等于集合O={o|o是从p出发密度可达的}
4 DBSCAN:Density Based Spatial Clustering of Applications with Noise
这一部分,我们提出了算法DBSCAN,用于在空间数据中根据定义5和定义6来发现聚类和噪声。理想地,我们必须知道每个聚类的合适的参数Eps和Minpts,一直相应聚类中的至少一个点。然后,我们用合适的参数取出所有从给定点密度可达的点。但是并没有好的方法给所有聚类提前获得这些信息。但是,有一个简单高效的方法heuristic(在4.2节提出),能确定Eps和MinPts的“thinnest”,如数据库中的最小密度和类。因此,DBSCAN使用全局的Eps和MinPts,即所有类都适用同一个值。“thinnest”类的密度参数是这个全局Eps和MinPts的值的最佳候选,定义了不是噪声点的最小密度。
4.1 The Algorithm
为了找到聚类,DBSCAN从任意一个p点开始,去从p出发的所有密度可达点(with respect Eps & MinPts)。如果p是core points,这个过程产生一个聚类。如果p是边界点,从p出发没有密度可达点,则DBSCAN选取数据集中的下一个点。
因为我们使用了一个全局的Eps和MinPts值,如果不同密度的类彼此很“接近”,DBSCAN可能根据定义5将两个类合并为一个类。定义两个点集的距离为S1和S2,记为dist(S1, S2)=min{dist(p,q)|p属于S1,q属于S2}。然后,当且仅当两个点集的距离大于Eps,这两个含有thinnest cluster密度的点集才会被拆分成两个集群。所以,可能需要递归调用DBSCAN,才会发现MinPts更高的类。然而,这不是缺点,因为DBSCAN的递归调用产生了非常有效的基本算法。此外,只有在易于检测的条件下才需要对簇的点进行递归聚类。
下面我们提出了一个基本版本的DBSCAN算法,忽略了数据类型以及cluster的额外信息。
SetOfPoints可以是整个数据集或者上一次聚类运行的结果。Eps和MinPts是全局密度参数,可以手动尝试,或者根据4.2提出的heuristics算法设定。函数SetOfPoints.get(i)返回SetOfPoints的第i个元素。DBSCAN使用的最重要的函数叫做ExpandCluster,这样写:
调用SetOfPoints.regionQuery(Points, Eps)会返回SetOfPoints中的点Point的Eps-Neighborhood链表。区域检测可以用空间搜索算法更高效地找到,例如R*-trees,这个方法在处理一些空间搜索问题很高效(Brinkhoff et al. 1994)。R
-tree的复杂度对于一个数据集的n个点再说最糟糕是O(log n),且具有“小”查询区域的查询必须仅遍历R -tree中的有限数量的路径。因为Eps-Neigborhood期望比较整个数据空间的一小部分数据,所以单一区域查询的平均运行时间复杂度是O(log n)。对数据集中的每n个点,我们最多进行一次区域查询。因此,DBSCAN的平均时间复杂度为O(nlog n)
如果数据集中一些点的密度可达发生改变,标记为噪声点的CLId(clusterId)集群也可能会发生改变。这种情况发生在集群的边界点中。这些点不会被加入seeds-list,因为我们已经知道标记为噪声点的ClID不是core point。将这些点加入seeds只会使区域搜索徒劳无功。
如果两个类C1和C2彼此非常接近,就可能一些点既属于C1又属于C2.这时候p一定是两者的边界点,因为如果不是边界点,C1和C2就会是一个类,因为我们用的全局参数。这种情况下,p会被分为先找到它的那个类。除了这种情况,DBSCAN的结果与访问数据集的点的顺序无关。
4.2 Determining the Parameters Eps and MinPts
在这一部分,我们用了一种简单但是很有效的heuristic(启发式)算法来确定数据集中“thinest”cluster的Eps和MinPts的Eps和MinPts参数。这种启发式算法是基于下面的observation。定义d为p到它的第k个最近邻的距离,那么几乎所有的点p的d-neighborhood都包含k+1个点。只有一些点到p的距离完全一样,d-neighborhood才会包含大于k+1个点,这种情况是几乎不可能的。此外,在一个类内更换一个点的k值不会导致d有太大的变化,除非p的第k个近邻k=1,2,3,...都位于一条直线上,但是这种情况通常不存在。
对于给定的k,定义函数k-dist为实数,代表将每个点到距离它第k个最近邻居的距离,对k-dist的值降序排序,这个函数图会给一些数据集密度的提示。我们把这个图叫做sorted k-dist graph。如果我们选择任意一个点p,设置参数Eps为k-dist(p),设置MinPts为k,所有相等或小于k-dist的点都是core points。如果我们能在“thinnest”cluster中找到一个有最大k-dist的阈值,就会得到我们想要的参数。这个阈值点就是排序过的k-dist图中第一个山谷值,见图4.所有k-dist较大的点(阈值左边)都认为是噪声,所有阈值右边的点认为是一些cluster。
通常来讲,很难自动发现第一个“山谷值”,但是在图像化后,人工看出山谷值会相对容易。因此,我们建议采用交互式方法来确定阈值点。
DBSCAN需要两个参数,Eps和MinPts。但是,我们的实验证明,k>4的k-dist图和4-dist图没有明显的差别,此外,它们还需要更大的计算量。因此,我们通过将所有数据库(对于2维数据)设置为4来消除参数MinPts。我们用下面的交互式方法决定DBSCAN的Eps:
- 系统计算并绘制数据集的4-dist图
- 如果用户能估计一定百分比的噪声,则输入此百分比,系统从中获取阈值点的建议。
- 用户可以选择接受建议或者用其他的阈值点。4-dist阈值被用作DBSCAN的Eps
5 Performance Evaluation
这一部分,我们评估了DBSCAN的表现。我们将它与CLARANS进行比较,因为它是为KDD设计的第一且唯一的聚类算法。在我们后续的研究中,将会与经典的基于密度的聚类算法进行比较。我们用C++实现了基于R*-tree的DBSCAN,所有实验在HP 735/100 工作站。我们使用了SEQUQIA2000基准集上的合成样本数据集。
为了比较DBSCAN和CLARANS的有效性(准确率),我们使用三个样本数据集,见图1。因为DBSCAN和CLARANS是不同类型的聚类算法,它们没有统一的分类准确度的定量测量方法,因此我们通过视觉评估两者的准确率。在样本数据集1,有4个形状的明显大小不一的聚类。样本数据2包含4个非凸形状的聚类。样本数据集3有4个不同形状的类,还有一些噪声。为了展示两种聚类算法的结果,我们用不同颜色可视化了每个cluster(见第6章后面的www availability)。为了让CLARANS表现好一些,我们将参数k设置为4。CLARANS发现的聚类见图5.
对DBSCAN,我们给样本集1和样本集2设置0%的噪声,给样本3设置10%的噪声。DBSCAN的聚类结果见图6.
DBSCAN发现了所有的cluster,且检测到了噪声点。但是CLARANS把一些相对大的cluster或者和其他类很近的cluster进行了拆分。此外,CLARANS没有区分出噪声,而是所有点都分配给了它们最接近的medoid。
为了测试DBSCAN和CLARANS的效率,我们使用SEQUOIA2000基准数据集。SEQUOIA2000使用了地球科学中用的实数集。有4种类型的数据:栅格数据,点数据,多边形数据和有向图数据。点数据有62584个Californian的地标名称以及它们的位置,取自US Geological Survey's Geographic Names Information System。点数据大概有2.1M。因为CLARANS在整个数据上运行时间很长,所以我们取SEQUIOA2000的子集进行实验,包含2%到20%的代表性数据。DBSCAN和CLARANS的运行时间比较见表1.
实验结果显示,DBSCAN的运行时间略高于线性数点。而CLARANS的运行时间接近二次方点。结果显示DBSCAN比CLARANS表现要好,随着数据集的增长,表现好250~1900倍。
6 Conclusions
聚类算法在解决空间数据分类问题中很常用。可是,众所周知的算法在应用于大型空间数据库时有严重的缺陷。本文提出一种聚类算法DBSCAN,依赖于clusters的密度概念。它只需要一个输入参数,支持用户自定义它的值。我们在SEQUOIA2000基准数据集上对其进行了评估。实验结果证明DBSCAN发现任意形状的聚类效果要明显好于CLARANS。此外,实验还证明了DBSCAN效率比CLARANS至少高100倍。
后续研究将考虑以下方向:首先,我们只考虑了点数据。可是空间数据集还有一些扩展对象,如四边形数据。我们需要发现四边形数据集在Eps-neighborhood上的密度,对DBSCAN进行泛化。其次,DBSCAN对高纬特征空间的应用也应该研究,特别是必须探索这种应用中k-dist图的形状。
WWW Availability
原文的URL点不开,就不放了……
![[翻译]A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise_第1张图片](http://img.e-com-net.com/image/info10/9f4c9244a89a45a889bcfe389bd2c43a.jpg)
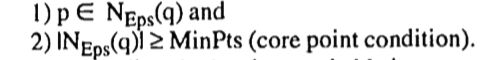
![[翻译]A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise_第2张图片](http://img.e-com-net.com/image/info10/943acb669f9143e5a7e53d62402d4af9.jpg)
![[翻译]A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise_第3张图片](http://img.e-com-net.com/image/info10/4b5f137a758b459e966ffa213a910d6e.jpg)
![[翻译]A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise_第4张图片](http://img.e-com-net.com/image/info10/e3a38d8fc8c54a0f8396f0ae206c6e90.jpg)
![[翻译]A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise_第5张图片](http://img.e-com-net.com/image/info10/50f7ccc742f644199d655b002d4c56b3.jpg)
![[翻译]A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise_第6张图片](http://img.e-com-net.com/image/info10/1defac566ee74a7c80412b08bee91560.jpg)
![[翻译]A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise_第7张图片](http://img.e-com-net.com/image/info10/c2095f785af5421584854847a8eb97f3.jpg)
![[翻译]A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise_第8张图片](http://img.e-com-net.com/image/info10/d16debe5f1e64a9ba919def630e956a1.jpg)
![[翻译]A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise_第9张图片](http://img.e-com-net.com/image/info10/8a9885b3f3f9455092a8ec890a3bc0f5.jpg)
![[翻译]A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise_第10张图片](http://img.e-com-net.com/image/info10/39f611730bdf493ca6621f376dce5923.jpg)