剑指offer - 顺时针打印矩阵 - JavaScript

题目描述

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字，例如，如果输入如下 4 X 4 矩阵： 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字 1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.

解法 1: 模拟路径

根据直觉，当遍历的过程中，遇到超出边界 / 元素已经被访问过的情况时，应该按照顺时针转变方向。

假设给定的矩阵的形状是 m*n，那么一共要遍历 m*n 次。要准备一个长度为 m*n 的哈希表，来保存元素是否被遍历过。要准备一个记录方向的数组，里面方向的排列顺序是顺时针。

时间复杂度为 O(M*N)，空间复杂度为 O(M*N)。

代码实现如下：

// ac地址：https://www.nowcoder.com/practice/9b4c81a02cd34f76be2659fa0d54342a
// 原文地址：https://xxoo521.com/2020-01-30-shun-shi-zhen-matrix/

/**
 * @param {number} i
 * @param {number} j
 */
function hash(i, j) {
    return `${i}-${j}`;
}

/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
function printMatrix(matrix) {
    const m = matrix.length;
    if (!m) {
        return [];
    }

    const n = matrix[0].length;
    if (!n) {
        return [];
    }

    const results = []; // 遍历结果
    const visited = {}; // 记录元素是否被访问过
    const directions = [
        [0, 1],
        [1, 0],
        [0, -1],
        [-1, 0]
    ]; // 顺时针方向数组

    for (let step = 0, row = 0, col = 0, dIdx = 0; step < m * n; ++step) {
        results.push(matrix[row][col]);
        visited[hash(row, col)] = true;
        // 最巧妙的地方：借助方向数组来进行row、col的更新
        const newR = row + directions[dIdx][0];
        const newC = col + directions[dIdx][1];

        if (
            !visited[hash(newR, newC)] &&
            newR >= 0 &&
            newR < m &&
            newC >= 0 &&
            newC < n
        ) {
            row = newR;
            col = newC;
        } else {
            // 转变方向
            dIdx = (dIdx + 1) % 4;
            row += directions[dIdx][0];
            col += directions[dIdx][1];
        }
    }

    return results;
}

解法 2: 按层遍历

这种方法的思路是从外到内，一层层打印。难点在于怎么找到标记点，以及防止重复遍历。

怎么找到标记点？对于每一层来说，设左上角的元素坐标为 (i, j)，那么右上角的元素坐标为 (i, n - j - 1)，右下角的元素坐标是 (m - i - 1 ,n - j - 1)，左下角的元素坐标是 (m - i - 1, j)。找到标记点后，就是对行/列进行+/-的过程。

怎么防止重复遍历？找到四个坐标点后，每一层的遍历可以拆分成 4 个部分。我想到的是下图所示的两种拆分方法：

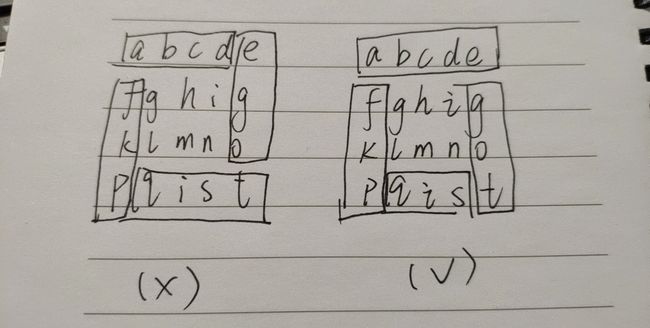
第一种拆分方法会有例外，比较难处理，无法避免重复遍历。因此使用第二种。

时间复杂度为 O(M*N)，空间复杂度为 O(M*N)。代码实现如下：

// ac地址：https://www.nowcoder.com/practice/9b4c81a02cd34f76be2659fa0d54342a
// 原文地址：https://xxoo521.com/2020-01-30-shun-shi-zhen-matrix/

/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
function printMatrix(matrix) {
    const m = matrix.length;
    if (!m) {
        return [];
    }

    const n = matrix[0].length;
    if (!n) {
        return [];
    }

    const results = [];
    let i = 0,
        j = 0;
    // 这里的终止条件是： i <= (m - 1) / 2 与 j <= (n - j) / 2
    // 即最里面的那层左上角元素的坐标
    while (i <= m - i - 1 && j <= n - j - 1) {
        for (let col = j; col <= n - j - 1; ++col) {
            results.push(matrix[i][col]);
        }

        for (let row = i + 1; row <= m - i - 1; ++row) {
            results.push(matrix[row][n - j - 1]);
        }

        if (i < m - i - 1 && j < n - j - 1) {
            for (let col = n - j - 2; col > j; --col) {
                results.push(matrix[m - i - 1][col]);
            }

            for (let row = m - i - 1; row > i; --row) {
                results.push(matrix[row][j]);
            }
        }

        i++;
        j++;
    }

    return results;
}

最后

1. 觉得不错， 帮忙点个推荐呗，您的支持是对我最大的激励
2. 欢迎我的公众号： 「心谭博客」，只专注于 前端 + 算法的原创分享

由于个人精力有限，很多系列和历史文章没有即时同步，请前往「前端图谱」&「算法题解」，保证您有所收获。