基础概念
数据(Data)
书上的是这样介绍的:
数据是描述客观事物的数值、字符以及能输入机器且能被处理的各种字符集。
我的理解为,举个栗子,我们全班的人员信息就是数据,其中的一个人员的信息也是数据。数字1也是数据,可以理解为用来描述的一些信息。
数据元素(Data Element)
书上的是这样介绍的:
数据元素是组成数据的基本单位,是数据集合的个体。
我的理解为,全班同学的信息为数据,那其中张三的信息就为全班数据中的一个数据元素。
数据对象(Data Object)
书上的是这样介绍的:
数据对象时性质相同的数据元素的集合,是数据的一个子集。
我的理解为,全班为一个集合,每个人员的信息就可以是一个数据对象。
数据结构
书上的是这样介绍的:
数据结构是指相互之间存在一种或者多种特定关系的数据元素集合,数据结构应该包括数据元素集合及元素间关系的集合,及数据的组织形式。
这里就可以理解为,树形结构呀,图形结构呀,线性结构呀等等。
数据结构的内容
数据元素之间的相互关系具体应该包括三个方面:
- 数据的逻辑结构
- 数据的存储结构
- 数据的运算集合
逻辑结构
数据的逻辑结构是指数据元素之间的逻辑关系描述。
根据数据之间关系的不同特性,通常有下列四类基本结构:
-
集合结构:结构中的数据元素之间除了属于一个集合的关系外,无任何关系,如图:
-
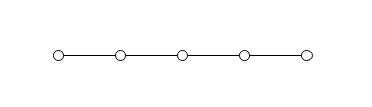
线性结构:结构中的数据元素之间存在着一对一的线性关系
-
树状结构:结构中的数据元素之间存在着一对多的层次关系
-
图状结构或网状结构:结构中的数据元素之间存在着多对多的任意关系
又可以根据集合关系只有属于或者不属于这种简单的属于关系,可以用其他的结构代替它,故数据的四类基本逻辑结构可概括为如下:
- 线性结构:线性表、栈、堆、队、字符串、数组、广义表
- 非线性结构:树、图
存储结构
存储结构(又称物理结构)是逻辑结构在计算机中的存储映像,包括数据元素映像和关系映像,它是逻辑结构在计算机中的实现。
逻辑结构与存储结构的关系为:存储结构是逻辑关系的映像与元素本身的映像。逻辑结构是数据结构的抽象,存储结构是数据结构的实现,两者综合起来建立了数据元素之间的结构关系。
数据元素之间的关系在计算机中有两种不同的表示方法:
- 顺序映像(顺序存储结构)
- 非顺序映像(非顺序存储结构)
运算集合
讨论数据结构的目的是为了在计算机中实现操作,因此在结构上的运算集合是很重要的部分。数据结构就是研究一类数据的表示及其相关的运算操作。
结合上面的内容,我们可以知道,按某种逻辑关系组织起来的一批数据,按一定的映像方式把它们存放在计算机的存储器中,并在这些数据上定义一个运算的集合,这些是数据结构课程的基本内容。
算法
算法 + 数据结构 = 程序,这说明数据结构和算法是程序的两大要素,二者相辅相成,缺一不可。
算法的定义
算法(Algorithm)是规则的有限集合,是为了解决特定问题而规定的一些列操作。
算法的特性
- 1、有限性:有限步骤之内正常结束,不能形成无穷循环。
- 2、确定性:算法中的每一个步骤必须要有确定含义,无二异性。
- 3、可行性:原则上能精确进行,操作可通过已实现的基本运算执行有限次而完成。
- 4、输入:有多个或者0个输入。
- 5、输出:至少有一个或者多个输出。
算法设计的要求
- 1、算法的正确性
- 2、可读性
- 3、健壮性(鲁棒性)
- 4、高效率和低存储量
算法的性能评价
评价算法性能的标准主要从算法的执行时间与占用存储空间两方面考虑,即算法执行所需的时间和存储空间来判断一个算法的优劣。
性能评估
对问题规模与该算法在运行时所占用空间与所耗时间给出一个数量关系的评价。
数量关系评价体现在时间上,即算法经编程实现后在计算机中所耗费的时间
数量关系评价体现在空间上,即算法经编程实现后在计算机中运行所占用的存储量。
问题规模
算法性能与问题规模相关。问题规模是问题大小的本质表示,对不同的问题其表现形式不同,算法求解问题的输入量称为问题的规模,一般用整数表示。比如:一个图论问题的规模则是图中的顶点数或边数;对于矩阵而言是其阶数;对于多项式运算而言是多项式项数;对集合而言是集合中的元素个数,可以说算法效率应该是问题规模的函数。
算法的时间性能分析
算法耗时的时间
一个算法的执行时间是指算法中所有语句执行时间的总和。每条语句的执行时间等于该条语句的执行次数乘以执行一次所需实际时间。但是由于不同计算机的性能不同,所以这个无法评价。
语句频度
度量一个算法的效率应当抛弃具体计算机条件,仅仅考虑算法本身的效率高低。算法时间分析度量的标准并不是针对实际执行时间精确算出执行的具体时间,而是根据算法中语句的执行次数做出估计,从中得到算法执行时间的信息。
语句频度是指该语句在一个算法中重复执行的次数。一个算法的时间耗费就是该算法中所有语句频度之和。如下列代码:
#include
#define n 100 /* n可根据需要定义,这里定为100 */
void MatrixMulti(int a[n][n],int b[n][n],int c[n][n])
{ //该算法每一语句的语句频度为
(1) for(i=0;i 语句1的循环控制变量i从0增加到n,测试条件i=n成立才会终止,故它的语句频度是n+1,但是它的循环体却只能执行n次。语句2作为语句1循环体内的语句应该执行n次,但是每次语句2本身要执行n+1次,所以语句2的频度是n(n+1)。同理可得语句3.4的频度。
所以,该算法中所有语句的频度之和为(即算法的时间耗费)
f(n) = 2n^3 + 3n^2 + 2n + 1
算法的时间复杂度
随着问题的规模n的增大,算法的执行时间的增长率和f(n)的增长率相同,称作算法的时间复杂度,如上算法,时间复杂度为O(n^3)
算法的空间性能分析
一般情况下,一个程序在机器上执行时,除了需要存储本身所用的指令、常数、变量和输入数据外,还需要一些对数据进行操作的辅助存储空间,其中,对于输入数据所占用的具体存储量取决于问题本身,与算法无关,这样子只需要分析该算法在实现时所需要的辅助空间单元个数。
算法耗费的空间
一个算法的占用空间是指算法实际占用的辅助空间总和。
由于实际占用与计算机的软件(编译系统)、硬件(字长等)环境密切相关,以整数为例,可能在一种系统中需要2个字节,在另外一个系统中需要4个字节,实际占用空间的多少难以相互类比。算法的空间分析度量的标准并不是计算实际占用空间,而是计算整个算法的辅助空间单元个数。
算法的空间复杂度
算法的空间复杂度定义为该算法所耗费的存储空间的数量级,它是问题规模n的函数。若算法执行时所需要的辅助空间相对于输入数据量而言是个常数,则称这个算法为原地工作,辅助空间为O(1)。如下:
问题:将一维数组a中的n个数据逆序存放到原数组中,给出实现该问题的两种算法。
[算法一]:
for(i=0;i[算法二]:
for(i=0;i其中,算法一的空间复杂度为O(n),需要一个大小为n的辅助数组b。
算法二的空间复杂度为O(1),仅需要一个变量t,与问题规模没有关系。
算法的时间复杂度和空间复杂度合称为算法的复杂度。