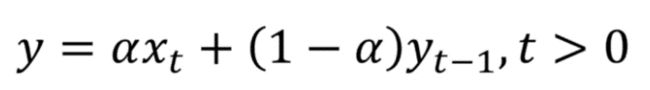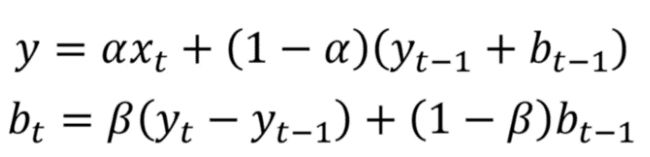文章发布于公号【数智物语】 (ID:decision_engine),关注公号不错过每一篇干货。
来源 | AI开发者(id:okweiwu)
作者 | 王雪佩
无论我们是想预测金融市场的趋势还是用电量,时间都是我们模型中必须考虑的一个重要因素。例如,预测一天中什么时候会出现用电高峰是很有趣的,可以以此为依据调整电价或发电量。
输入时间序列。时间序列只是按时间顺序排列的一系列数据点。在时间序列中,时间往往是独立变量,其目标通常是预测未来。
然而,在处理时间序列时,还有一些其他因素会发挥作用。
它是静止的吗?
有季节性吗?
目标变量是否自相关?
在这篇文章中,我将介绍时间序列的不同特征,以及我们如何对它们进行建模才能获得准确的预测。
预测未来是困难的
01
自相关
通俗地说,自相关是观测值之间的相似度,它是观测值之间时间滞后的函数。
自相关示例
上面是一个自相关的例子。仔细观察,你会发现第一个值和第 24 个值具有很高的自相关性。同样,第 12 个值和第 36 个观测值也高度相关。这意味着我们将在每 24 个时间单位中找到一个非常相似的值。
注意,这个图看起来像正弦函数。这是季节性的征兆,你可以通过在上面的图中找到 24 小时的周期来找到它的价值。
02
季节性
季节性是指周期性波动。例如,白天的用电量高,晚上的用电量低,或者圣诞节期间的在线销售额增加,节后销售再次放缓。
季节性示例
如你所见,每天都有明显的季节性。每天晚上,你都会看到一个高峰,最低点出现在每天的开始和结束。
记住,如果季节性是满足正弦函数的,它也可以从自相关图中推导出来。简单地看一下周期,它给出了季节的长度。
03
平稳性
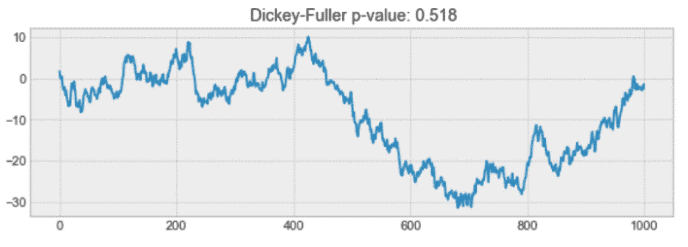
平稳性是时间序列的一个重要特征。如果时间序列的统计性质不随时间变化,则称其为平稳的。换句话说,它有不变的均值和方差,协方差不随时间变化。
平稳过程示例
再看上面的图,我们看到上面的过程是平稳的,平均值和方差不会随时间变化。
通常,股票价格不是一个平稳的过程,因为我们可能会看到一个增长的趋势,或者,其波动性可能会随着时间的推移而增加(这意味着方差正在变化)。
理想情况下,我们需要一个用于建模的固定时间序列。当然,不是所有的都是平稳的,但是我们可以通过做不同的变换,使它们保持平稳。
04
如何测试过程是否平稳
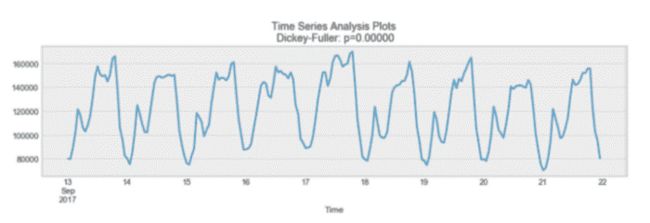
你可能已经注意到在上图的标题「Dickey-Fuller」。这是我们用来确定时间序列是否稳定的统计测试。
在不讨论 Dickey-Fuller 测试的技术特性的情况下,它检测了单位根是否存在空假设。
如果是,则 P>0,并且过程不是平稳的。
否则,p=0,无效假设被拒绝,过程被认为是平稳的。
例如,下面的过程不是平稳的。请注意为什么平均值不随时间变化。
非平稳过程示例
05
时间序列建模
有很多方法可以模拟时间序列来进行预测。在此,我将介绍:
1. 移动平均
2. 指数平滑
3. ARIMA
01
移动平均
移动平均模型可能是最简单的时间序列建模方法。这个模型简单来说就是,下一个值是所有过去值的平均值。
虽然很简单,但是这个模型的效果可能好到出乎意料,它代表了一个好的起点。
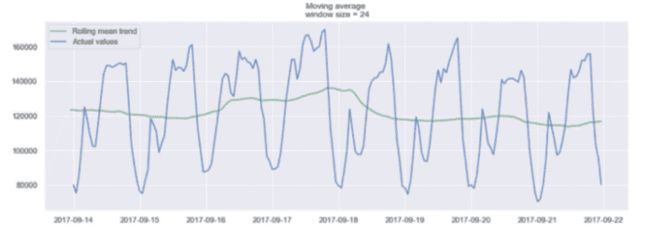
否则,移动平均值可用于识别数据中有趣的趋势。我们可以定义一个窗口来应用移动平均模型来平滑时间序列,并突出不同的趋势。
24 小时窗口上的移动平均值示例
在上面的图中,我们将移动平均模型应用于一个 24 小时窗口。绿线平滑了时间序列,我们可以看到 24 小时内有 2 个峰值。
当然,窗口越长,趋势就越平滑。下面是一个较小窗口上移动平均值的示例。
12 小时窗口上的移动平均值示例
02
指数平滑
指数平滑使用与移动平均相似的逻辑,但这次,对每个观测值分配了不同的递减权重。换言之,离现在的时间距离越远,观察结果的重要性就越低。
在数学上,指数平滑表示为:
指数平滑表达式
这里,alpha 是一个平滑因子,它的值介于 0 和 1 之间。它决定了之前观测值的权重下降的速度。
指数平滑示例
在上面的图中,深蓝色线表示时间序列的指数平滑,平滑系数为 0.3,而橙色线表示平滑系数为 0.05。
如你所见,平滑因子越小,时间序列就越平滑。这是有意义的,因为当平滑因子接近 0 时,我们接近移动平均模型。
03
双指数平滑
当时间序列中存在趋势时,使用双指数平滑。在这种情况下,我们使用这种技术,它只是指数平滑的两次递归使用。
数学公式为:
双指数平滑表达式
这里,beta 是趋势平滑因子,它的值介于 0 和 1 之间。
下面,你可以看到 alpha 和 beta 的不同值如何影响时间序列的形状。
双指数平滑示例
04
三指数平滑
该方法通过添加季节平滑因子来扩展双指数平滑。当然,如果你注意到时间序列中的季节性,这很有用。
在数学上,三指数平滑表示为:
三指数平滑表达式
其中 gamma 是季节平滑因子,L 是季节长度。
06
季节性差分自回归滑动平均模型(SARIMA)
SARIMA 实际上是简单模型的组合,可以生成一个复杂的模型,该模型可以模拟具有非平稳特性和季节性的时间序列。
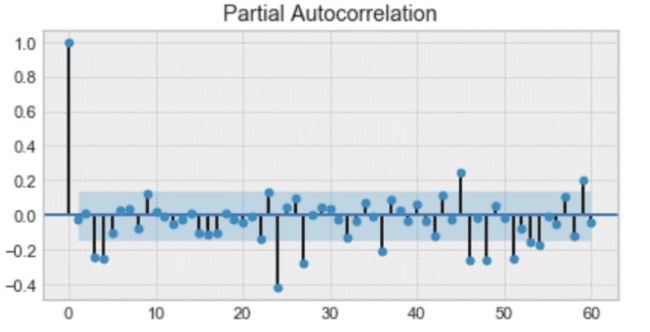
首先,我们得到了自回归模型 AR(p)。这基本上是时间序列对自身的回归。在这里,我们假设当前值依赖于它以前的值,并且有一定的滞后。它采用一个表示最大滞后的参数 p。为了找到它,我们查看了部分自相关图,在此之后大部分滞后并不显著。
在下面的例子中,p 的值是 4。
部分自相关图示例
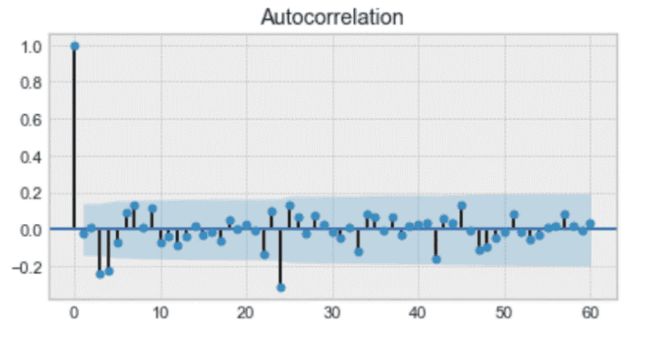
然后,我们添加移动平均模型 MA(q)。这需要一个参数 q,它代表自相关图上那些滞后不显著的最大滞后。
下图中,q 为 4。
自相关图示例
之后,我们添加整合顺序 I(d)。参数 d 表示使序列平稳所需的差异数。
最后,我们添加最后一部分:季节性 S(P, D, Q, s),其中 S 只是季节的长度。此外,这里要求参数 P 和 Q 与 p 和 q 相同,但用于季节部分。最后,D 是季节整合的顺序,表示从系列中删除季节性所需的差异数量。
综合起来,我们得到了 SARIMA(p, d, q)(P, D, Q, s) 模型。
要注意的是:在用 SARIMA 建模之前,我们必须对时间序列进行转换,以消除季节性和任何非平稳行为。
这是一个很好的理论!让我们在第一个项目中应用上面讨论的技术。
我们将想办法预测一家公司的股票价格。现在,预测股票价格几乎是不可能的。然而,这仍然是一个有趣的练习,它将是一个很好的来实践我们所学到知识的方法。
07
项目 1:股票价格预测
我们将利用 New Germany Fund(GF)的历史股价来预测未来五个交易日的收盘价。
你可以在这里获取数据集和资料。
像往常一样,我强烈推荐你动手编码!启动你的笔记本,我们开始吧!
你绝不会因为这个项目而发财
01
导入数据
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
from sklearn.metrics import r2_score, median_absolute_error, mean_absolute_error
from sklearn.metrics import median_absolute_error, mean_squared_error, mean_squared_log_error
from scipy.optimize import minimize
import statsmodels.tsa.api as smt
import statsmodels.api as sm
from tqdm import tqdm_notebook
from itertools import product
def mean_absolute_percentage_error(y_true, y_pred):
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
DATAPATH = 'data/stock_prices_sample.csv'
data = pd.read_csv(DATAPATH, index_col=['DATE'], parse_dates=['DATE'])
data.head(10)
首先,我们导入一些库,这些库将在整个分析过程中都会用到。此外,我们用平均百分比误差(MAPE)作为我们的误差度量。
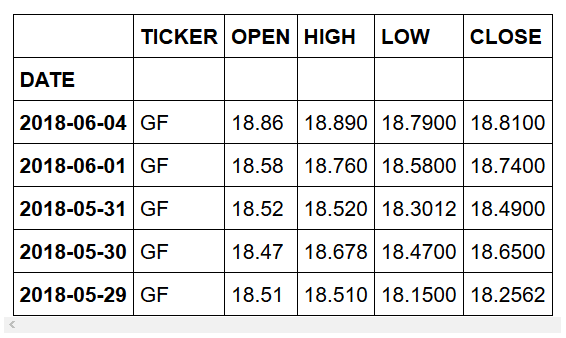
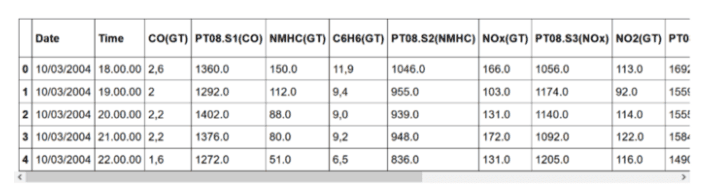
然后,我们导入数据集,排在前十的是:
数据集的前 10 个条目
正如你所看到的,我们有一些关于 New Germany Fund (GF) 不同股票的数据。此外,我们还有一个关于当天信息的数据,但我们只需要当天结束(EOD)时的股票信息。
02
数据清洗
data = data[data.TICKER != 'GEF']
data = data[data.TYPE != 'Intraday']
drop_cols = ['SPLIT_RATIO', 'EX_DIVIDEND', 'ADJ_FACTOR', 'ADJ_VOLUME', 'ADJ_CLOSE', 'ADJ_LOW', 'ADJ_HIGH', 'ADJ_OPEN', 'VOLUME', 'FREQUENCY', 'TYPE', 'FIGI']
data.drop(drop_cols, axis=1, inplace=True)
data.head()
首先,我们删除不需要的条目。
然后,我们删除不需要的列,因为我们只想关注股票的收盘价。
如果预览数据集,则应该看到的是:
清洗后的数据集
令人惊叹!我们准备好进行探索性数据分析了!
03
探索性数据分析(EDA)
# Plot closing price
plt.figure(figsize=(17, 8))
plt.plot(data.CLOSE)
plt.title('Closing price of New Germany Fund Inc (GF)')
plt.ylabel('Closing price ($)')
plt.xlabel('Trading day')
plt.grid(False)
plt.show()
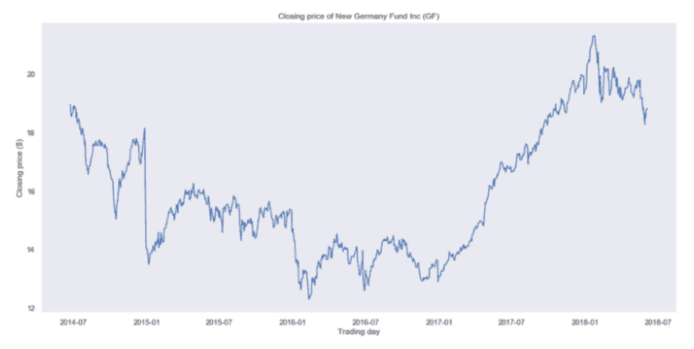
我们绘制数据集整个时间段的收盘价。你将会得到:
New Germany Fund (GF)收盘价
很明显,你看到的不是一个平稳的过程,很难判断是否有某种季节性。
04
移动平均
让我们使用移动平均模型来平滑我们的时间序列。为此,我们将使用一个辅助函数,该函数将在指定的时间窗口上运行移动平均模型,并绘制结果平滑曲线:
def plot_moving_average(series, window, plot_intervals=False, scale=1.96):
rolling_mean = series.rolling(window=window).mean()
plt.figure(figsize=(17,8))
plt.title('Moving average\n window size = {}'.format(window))
plt.plot(rolling_mean, 'g', label='Rolling mean trend')
#Plot confidence intervals for smoothed values
if plot_intervals:
mae = mean_absolute_error(series[window:], rolling_mean[window:])
deviation = np.std(series[window:] - rolling_mean[window:])
lower_bound = rolling_mean - (mae + scale * deviation)
upper_bound = rolling_mean + (mae + scale * deviation)
plt.plot(upper_bound, 'r--', label='Upper bound / Lower bound')
plt.plot(lower_bound, 'r--')
plt.plot(series[window:], label='Actual values')
plt.legend(loc='best')
plt.grid(True)
#Smooth by the previous 5 days (by week)
plot_moving_average(data.CLOSE, 5)
#Smooth by the previous month (30 days)
plot_moving_average(data.CLOSE, 30)
#Smooth by previous quarter (90 days)
plot_moving_average(data.CLOSE, 90, plot_intervals=True)
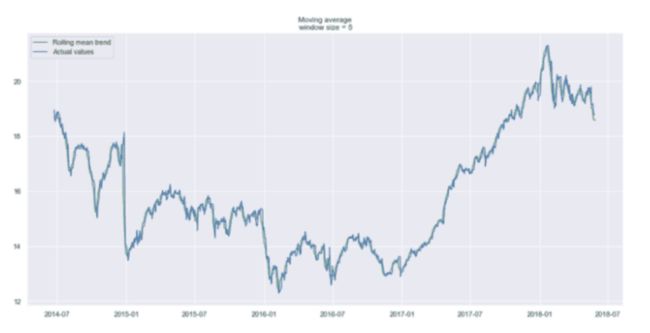
使用5天的时间窗口,我们得到:
上一个交易周的平滑曲线
如你所见,我们几乎看不到趋势,因为它太接近实际曲线。让我们看看上个月和上个季度的平滑处理结果。
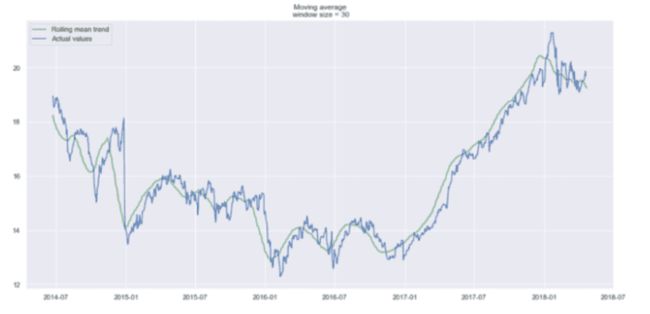
上个月(30 天前)的平滑曲线
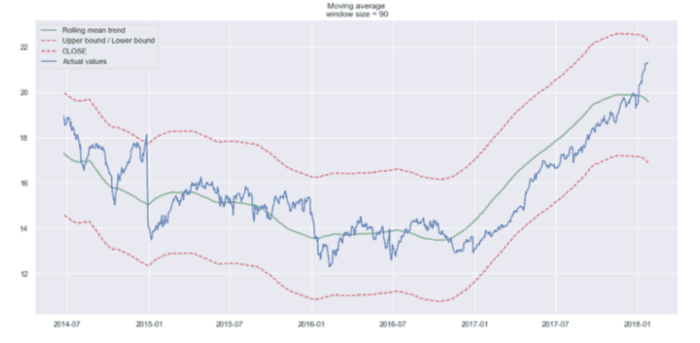
按上一季度(90 天)平滑
现在更容易发现趋势。请注意,30 天和 90 天的趋势图在末尾显示一条向下的曲线。这意味着股票可能在接下来的几天内会下跌。
05
指数平滑
现在,让我们用指数平滑来看看它是否能获得更好的趋势。
def exponential_smoothing(series, alpha):
result = [series[0]] # first value is same as series
for n in range(1, len(series)):
result.append(alpha * series[n] + (1 - alpha) * result[n-1])
return result
def plot_exponential_smoothing(series, alphas):
plt.figure(figsize=(17, 8))
for alpha in alphas:
plt.plot(exponential_smoothing(series, alpha), label="Alpha {}".format(alpha))
plt.plot(series.values, "c", label = "Actual")
plt.legend(loc="best")
plt.axis('tight')
plt.title("Exponential Smoothing")
plt.grid(True);
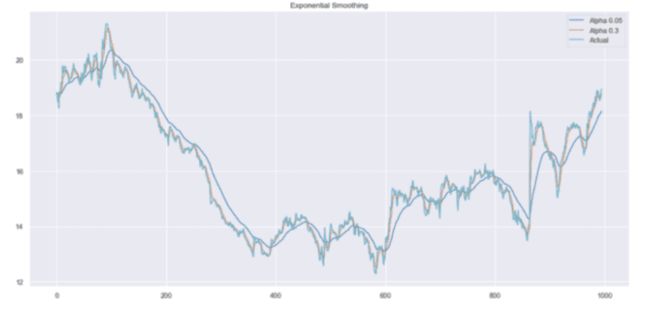
plot_exponential_smoothing(data.CLOSE, [0.05, 0.3])
这里,我们使用 0.05 和 0.3 作为平滑因子的值。当然你也可以尝试其他值,看看结果如何。
指数平滑
如您所见,alpha 值 0.05 平滑了曲线,同时剔除了大部分向上和向下的趋势。
现在,让我们使用双指数平滑。
06
双指数平滑
def double_exponential_smoothing(series, alpha, beta):
result = [series[0]]
for n in range(1, len(series)+1):
if n == 1:
level, trend = series[0], series[1] - series[0]
if n >= len(series): # forecasting
value = result[-1]
else:
value = series[n]
last_level, level = level, alpha * value + (1 - alpha) * (level + trend)
trend = beta * (level - last_level) + (1 - beta) * trend
result.append(level + trend)
return result
def plot_double_exponential_smoothing(series, alphas, betas):
plt.figure(figsize=(17, 8))
for alpha in alphas:
for beta in betas:
plt.plot(double_exponential_smoothing(series, alpha, beta), label="Alpha {}, beta {}".format(alpha, beta))
plt.plot(series.values, label = "Actual")
plt.legend(loc="best")
plt.axis('tight')
plt.title("Double Exponential Smoothing")
plt.grid(True)
plot_double_exponential_smoothing(data.CLOSE, alphas=[0.9, 0.02], betas=[0.9, 0.02])
你将得到:
双指数平滑
同样,用不同的 α 和 β 组合进行实验,以获得更好的曲线。
07
建模
如前所述,我们必须将序列转换为一个平稳的过程,以便对其进行建模。因此,让我们应用 Dickey-Fuller 测试来看看它是否是一个平稳的过程:
def tsplot(y, lags=None, figsize=(12, 7), syle='bmh'):
if not isinstance(y, pd.Series):
y = pd.Series(y)
with plt.style.context(style='bmh'):
fig = plt.figure(figsize=figsize)
layout = (2,2)
ts_ax = plt.subplot2grid(layout, (0,0), colspan=2)
acf_ax = plt.subplot2grid(layout, (1,0))
pacf_ax = plt.subplot2grid(layout, (1,1))
y.plot(ax=ts_ax)
p_value = sm.tsa.stattools.adfuller(y)[1]
ts_ax.set_title('Time Series Analysis Plots\n Dickey-Fuller: p={0:.5f}'.format(p_value)) smt.graphics.plot_acf(y, lags=lags, ax=acf_ax) smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax) plt.tight_layout()
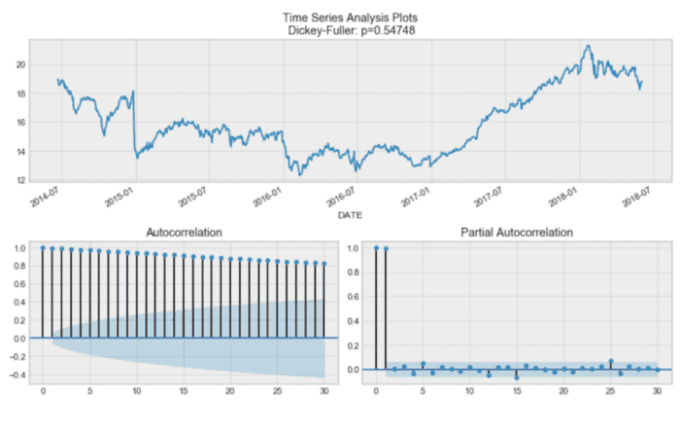
tsplot(data.CLOSE, lags=30)
# Take the first difference to remove to make the process stationary
data_diff = data.CLOSE - data.CLOSE.shift(1)
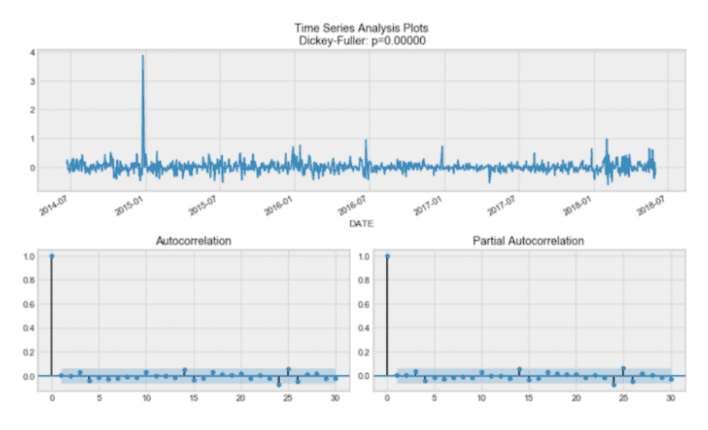
tsplot(data_diff[1:], lags=30)
你将看到:
通过 DickeyFuller 测试,时间序列是非平稳的。另外,从自相关图来看,我们发现它似乎没有明显的季节性。
因此,为了消除高度自相关并使过程稳定,让我们取第一个差异(代码块中的第 23 行)。我们简单地用一天的滞后时间减去时间序列,得到:
令人惊叹的!我们的序列现在是平稳的,可以开始建模了!
08
SARIMA
#Set initial values and some bounds
ps = range(0, 5)
d = 1
qs = range(0, 5)
Ps = range(0, 5)
D = 1
Qs = range(0, 5)
s = 5
#Create a list with all possible combinations of parameters
parameters = product(ps, qs, Ps, Qs)
parameters_list = list(parameters)
len(parameters_list)
# Train many SARIMA models to find the best set of parameters
def optimize_SARIMA(parameters_list, d, D, s):
"""
Return dataframe with parameters and corresponding AIC
parameters_list - list with (p, q, P, Q) tuples
d - integration order
D - seasonal integration order
s - length of season
"""
results = []
best_aic = float('inf')
for param in tqdm_notebook(parameters_list):
try: model = sm.tsa.statespace.SARIMAX(data.CLOSE, order=(param[0], d, param[1]),
seasonal_order=(param[2], D, param[3], s)).fit(disp=-1)
except:
continue
aic = model.aic
#Save best model, AIC and parameters
if aic < best_aic:
best_model = model
best_aic = aic
best_param = param
results.append([param, model.aic])
result_table = pd.DataFrame(results)
result_table.columns = ['parameters', 'aic']
#Sort in ascending order, lower AIC is better
result_table = result_table.sort_values(by='aic', ascending=True).reset_index(drop=True)
return result_table
result_table = optimize_SARIMA(parameters_list, d, D, s)
#Set parameters that give the lowest AIC (Akaike Information Criteria)
p, q, P, Q = result_table.parameters[0]
best_model = sm.tsa.statespace.SARIMAX(data.CLOSE, order=(p, d, q),
seasonal_order=(P, D, Q, s)).fit(disp=-1)
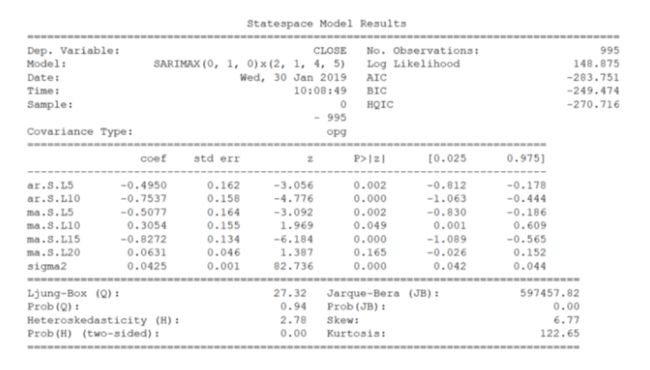
print(best_model.summary())
现在,对于 SARIMA,我们首先定义一些参数值的范围,以生成 p, q, d, P, Q, D, s 的所有可能组合的列表。
现在,在上面的代码单元中,我们有 625 种不同的组合!我们将尝试每种组合,并训练 SARIMA,以便找到性能最佳的模型。这可能需要一些时间,具体多长时间取决于计算机的处理能力。
完成后,我们将输出最佳模型的摘要,你将看到:
令人惊叹!最后,我们预测未来五个交易日的收盘价,并评估模型的 MAPE。
在这种情况下,有一个 0.79% 的 MAPE,这是非常好的!
09
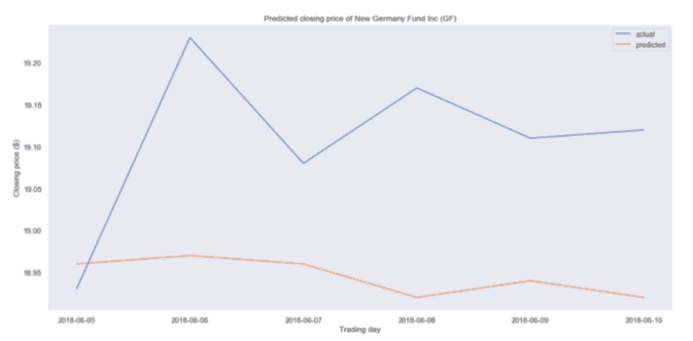
将预测价格与实际数据进行比较
# Make a dataframe containing actual and predicted prices
comparison = pd.DataFrame({'actual': [18.93, 19.23, 19.08, 19.17, 19.11, 19.12],
'predicted': [18.96, 18.97, 18.96, 18.92, 18.94, 18.92]},
index = pd.date_range(start='2018-06-05', periods=6,))
#Plot predicted vs actual price
plt.figure(figsize=(17, 8))
plt.plot(comparison.actual)
plt.plot(comparison.predicted)
plt.title('Predicted closing price of New Germany Fund Inc (GF)')
plt.ylabel('Closing price ($)')
plt.xlabel('Trading day')
plt.legend(loc='best')
plt.grid(False)
plt.show()
现在,为了将我们的预测与实际数据进行比较,我们从雅虎财务(YahooFinance)获取财务数据并创建一个数据框架。
然后,我们绘出曲线,看看我们与实际收盘价的差距有多大:
预计值和实际收盘价比较
我们的预测似乎有点偏离。事实上,预测价格很平稳,这意味着我们的模型可能表现不佳。
当然,这不是因为我们的程序,而是因为预测股票价格基本上是不可能的。
从第一个项目开始,我们学习了在使用 SARIMA 建模之前平滑时间序列的整个过程。
现在,让我们介绍一下 Facebook 的 Prophet。它是一个在 python 和 r 中都可用的预测工具。该工具帮助生成高质量的预测。
让我们看看如何在第二个项目中使用它!
08
项目2-使用 Prophet 预测空气质量
标题说明了一切:我们将使用 Prophet 来帮助我们预测空气质量!
01
导入数据
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
from scipy import stats
import statsmodels.api as sm
import matplotlib.pyplot as plt
%matplotlib inline
DATAPATH = 'data/AirQualityUCI.csv'
data = pd.read_csv(DATAPATH, sep=';')
data.head()
打印出前五行:
如你所见,数据集包含有关不同气体浓度的信息。每天隔一个小时记录一次。
如果更深入地研究数据集,会发现有许多值 -200 的实例。当然,负浓度是没有意义的,所以我们需要在建模前清洗数据。
02
数据清洗与特征工程
# Make dates actual dates
data['Date'] = pd.to_datetime(data['Date'])
# Convert measurements to floats
for col in data.iloc[:,2:].columns:
if data[col].dtypes == object:
data[col] = data[col].str.replace(',', '.').astype('float')
# Compute the average considering only the positive values
def positive_average(num):
return num[num > -200].mean()
# Aggregate data
daily_data = data.drop('Time', axis=1).groupby('Date').apply(positive_average)
# Drop columns with more than 8 NaN
daily_data = daily_data.iloc[:,(daily_data.isna().sum() <= 8).values]
# Remove rows containing NaN values
daily_data = daily_data.dropna()
# Aggregate data by week
weekly_data = daily_data.resample('W').mean()
# Plot the weekly concentration of each gas
def plot_data(col):
plt.figure(figsize=(17, 8))
plt.plot(weekly_data[col])
plt.xlabel('Time')
plt.ylabel(col)
plt.grid(False)
plt.show()
for col in weekly_data.columns:
plot_data(col)
在这里,我们首先分析日期列,将其转换为日期类型。
然后,我们把所有的测量值转换成浮点数。
之后,我们用每天的平均值来汇总数据。
我们还有一些需要删除的 NAN。
最后,我们按周汇总数据,这将提供一个更平滑的分析趋势。
我们可以画出每种化学物质浓度的趋势。这里,我们展示了 NOx。
NOx 浓度
氮氧化物是非常有害的,因为它们会形成烟雾和酸雨,同时也会形成细颗粒和臭氧。这些都会对健康产生不利影响,因此氮氧化物的浓度是空气质量的一个关键特征。
03
建模
# Drop irrelevant columns
cols_to_drop = ['PT08.S1(CO)', 'C6H6(GT)', 'PT08.S2(NMHC)', 'PT08.S4(NO2)', 'PT08.S5(O3)', 'T', 'RH', 'AH']
weekly_data = weekly_data.drop(cols_to_drop, axis=1)
# Import Prophet
from fbprophet import Prophet
import logging
logging.getLogger().setLevel(logging.ERROR)
# Change the column names according to Prophet's guidelines
df = weekly_data.reset_index()
df.columns = ['ds', 'y']
df.head()
# Split into a train/test set
prediction_size = 30
train_df = df[:-prediction_size]
# Initialize and train a model
m = Prophet()
m.fit(train_df)
# Make predictions
future = m.make_future_dataframe(periods=prediction_size)
forecast = m.predict(future)
forecast.head()
# Plot forecast
m.plot(forecast)
# Plot forecast's components
m.plot_components(forecast)
# Evaluate the model
def make_comparison_dataframe(historical, forecast):
return forecast.set_index('ds')[['yhat', 'yhat_lower', 'yhat_upper']].join(historical.set_index('ds'))
cmp_df = make_comparison_dataframe(df, forecast)
cmp_df.head()
def calculate_forecast_errors(df, prediction_size):
df = df.copy()
df['e'] = df['y'] - df['yhat']
df['p'] = 100 * df['e'] / df['y']
predicted_part = df[-prediction_size:]
error_mean = lambda error_name: np.mean(np.abs(predicted_part[error_name]))
return {'MAPE': error_mean('p'), 'MAE': error_mean('e')}
for err_name, err_value in calculate_forecast_errors(cmp_df, prediction_size).items():
print(err_name, err_value)
# Plot forecast with upper and lower bounds
plt.figure(figsize=(17, 8))
plt.plot(cmp_df['yhat'])
plt.plot(cmp_df['yhat_lower'])
plt.plot(cmp_df['yhat_upper'])
plt.plot(cmp_df['y'])
plt.xlabel('Time')
plt.ylabel('Average Weekly NOx Concentration')
plt.grid(False)
plt.show()
我们将只关注氮氧化物浓度。因此,我们删除所有其他不相关的列。
然后,我们导入 Prophet。
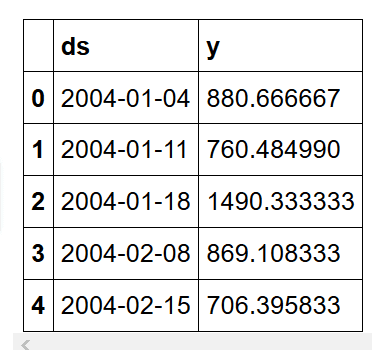
Prophet 要求日期列命名为 ds,特征列命名为 y,因此我们进行了适当的更改。
此时,我们的数据如下:
然后,我们定义一个训练集。为此,我们将保留最后 30 个条目进行预测和验证。
之后,我们简单地初始化 Prophet,将模型与数据匹配,并进行预测!
你会看到:
这里,yhat 代表预测值,yhat_lower 和 yhat_upper 分别代表预测值的下限和上限。
Prophet 让你可以轻松绘制预测图,我们得到:
NOx 浓度预测
如你所见,Prophet 只是用一条直线来预测未来的 NOx 浓度。
然后,我们检查时间序列是否具有某些有趣的特性,例如季节性:
在这里,Prophet 没有发现季节性的趋势。
通过计算模型的平均绝对百分误差(MAPE)和平均绝对误差(MAE)来评估模型的性能,我们发现 MAPE 为 13.86%,MAE 为 109.32,这还不错!记住,我们根本没有对模型进行微调。
最后,我们只需绘制预测的上限和下限:
每周 NOx 平均浓度预测
恭喜你达到目的!这篇文章很长,但内容丰富。你学会了如何强有力地分析和建模时间序列,并将你的知识应用到两个不同的项目中。我希望你觉得这篇文章有用。
via:https://towardsdatascience.com/the-complete-guide-to-time-series-analysis-and-forecasting-70d476bfe775
星标我,每天多一点智慧