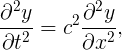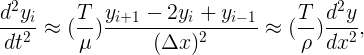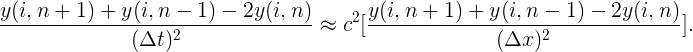1. Abstract
- EXERCISES
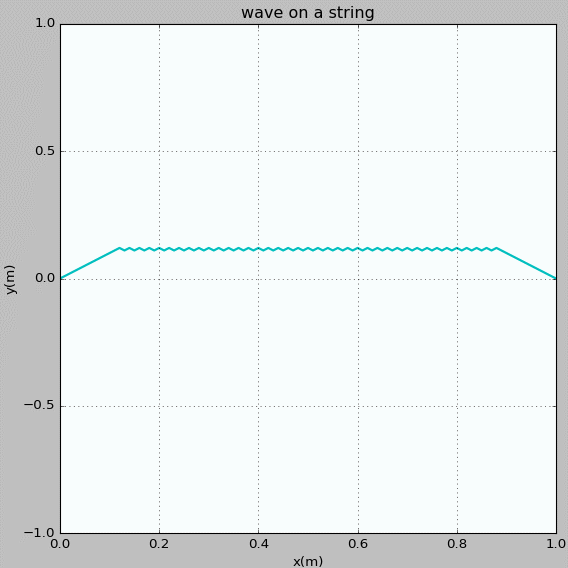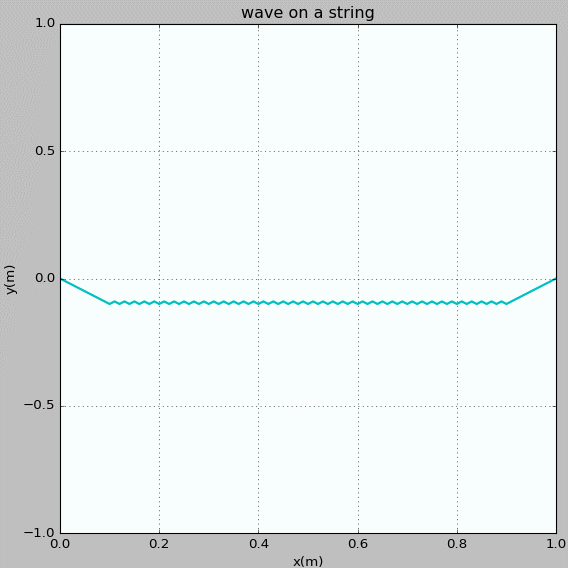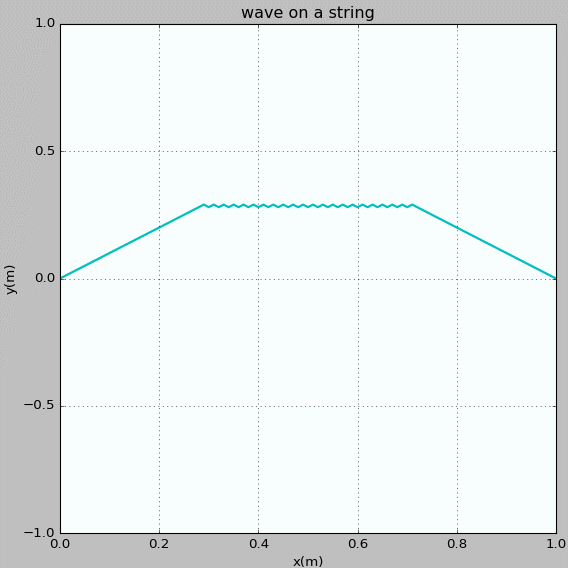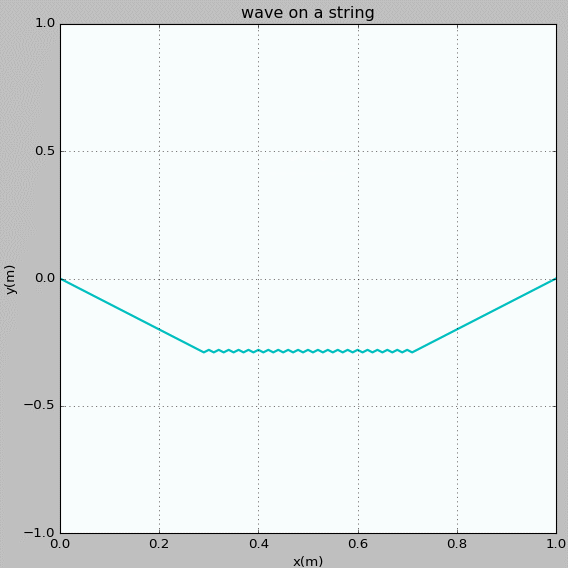
6.12. Gaussian initial string displacements are convenient for the calculations of this section, but are not very realistic. When a real string, such as a guitar string, is plucked, the initial string displacement is more accurately described by two straight lines that start at the ends of the string (we assume fixed ends) and end at the excitation point, as illustrated in Figure 6.4. Compare the power spectrum for a string excited in this manner with the results found above for a Gaussian initial wavepacket.
2. Background
§ 2.1 Wave
In physics, a wave is an oscillation accompanied by a transfer of energy that travels through a medium (space or mass). Frequency refers to the addition of time. Wave motion transfers energy from one point to another, which displace particles of the transmission medium–that is, with little or no associated mass transport. Waves consist, instead, of oscillations or vibrations (of a physical quantity), around almost fixed locations.
§ 2.1.1 Mechanical Wave
A mechanical wave is a wave that is an oscillation of matter, and therefore transfers energy through a medium.[1] While waves can move over long distances, the movement of the medium of transmission—the material—is limited. Therefore, oscillating material does not move far from its initial equilibrium position. Mechanical waves transport energy. This energy propagates in the same direction as the wave. Any kind of wave (mechanical or electromagnetic) has a certain energy. Mechanical waves can be produced only in media which possess elasticity and inertia.
§ 2.1.1.1 Waves On Strings
A vibration in a string is a wave. Resonance causes a vibrating string to produce a sound with constant frequency, i.e. constant pitch. If the length or tension of the string is correctly adjusted, the sound produced is a musical note. Vibrating strings are the basis of string instruments such as guitars, cellos, and pianos.
3. Main
§ 3.1 Formulation
The central equation of wave motion is
which is usually referred to as the wave equation. c is a parameter that turns out to be the speed with which a wave moves on the string.
The wave equation can be derived readily in the following procedures:
and then use a finite difference approximation for the angles
We obtain
which is precisely of the form of the wave equation.
Write it in finite difference form, yields
Rearrange it and we have the result
where r ≡ cΔt/Δx.
And we fix c = 1 in our problem and get
For ''Gaussian pluck'' of the string, we have
§ 3.2 Results
**The string had a length of 1 m and the simulation used the values c = 300 m/s, Δx = 0.01m, and Δt = Δx/c. **
§ 3.2.1 Results for waves on strings excited with different initial plucks (with fixed ends)
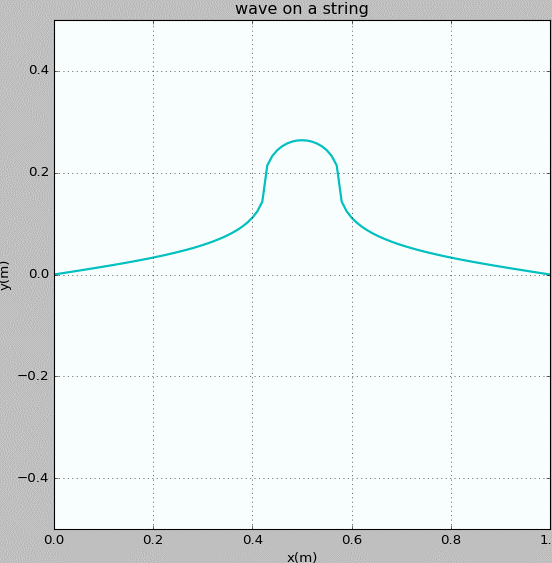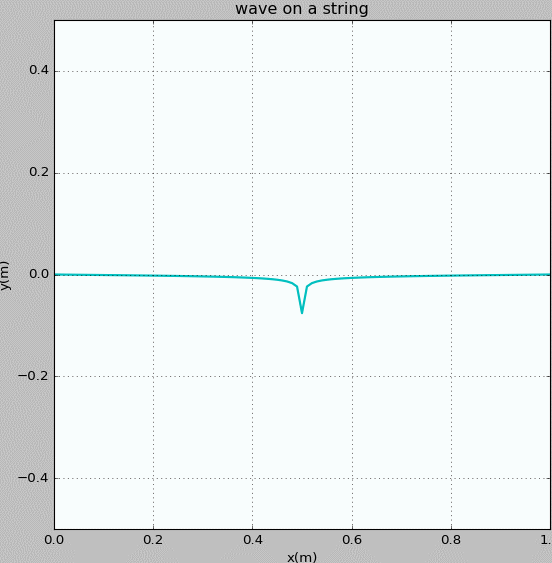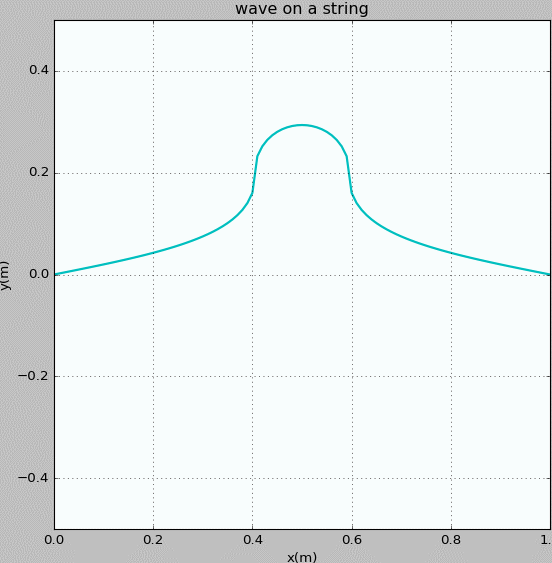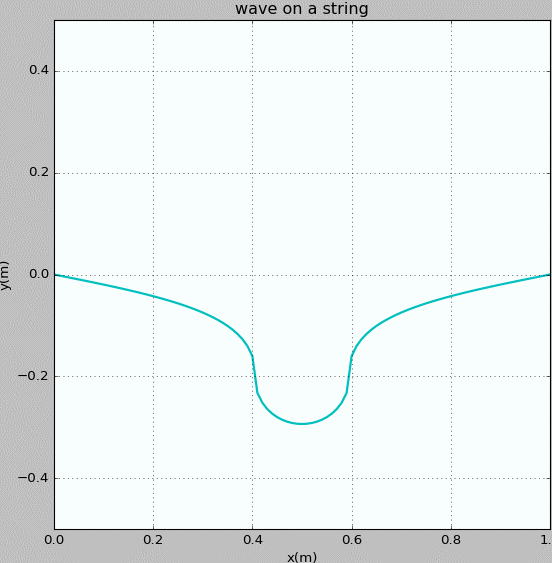
Figure 1: Waves propagating on a string with fixed ends. The initial pluck is a Gaussian wave pocket.
Figure 2: Waves propagating on a string with fixed ends. The initial pluck is three Gaussian wave pocket.
Figure 3: Waves propagating on a string with fixed ends. The initial pluck is a semicircle whose radius is 0.5 m.
Figure 4: Waves propagating on a string with fixed ends. The initial pluck is a semicircle whose radius is 0.25 m and whose origin is at x = 0.3 m.
It is kind of pathological, so let's us slow it down at the beginning of the propagation of the wave to see more clearly what happend.
Figure 5: Slow playback of Figure 4.
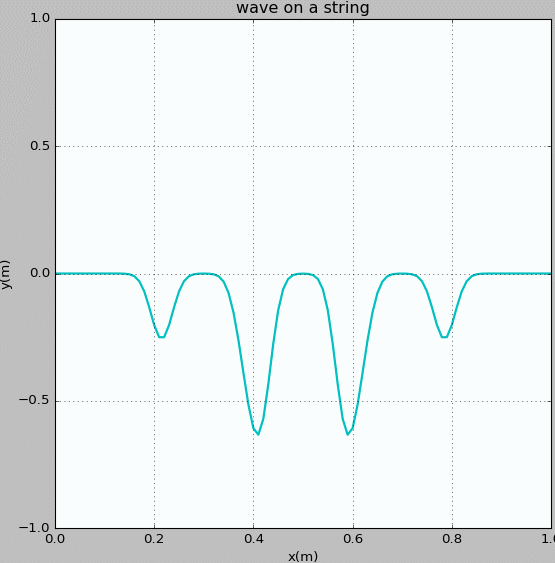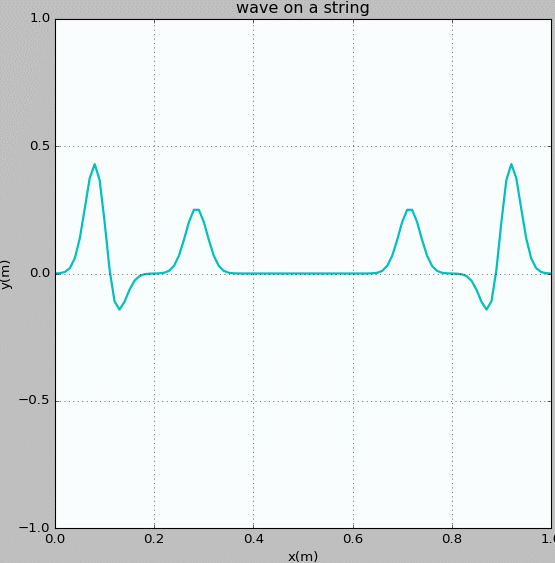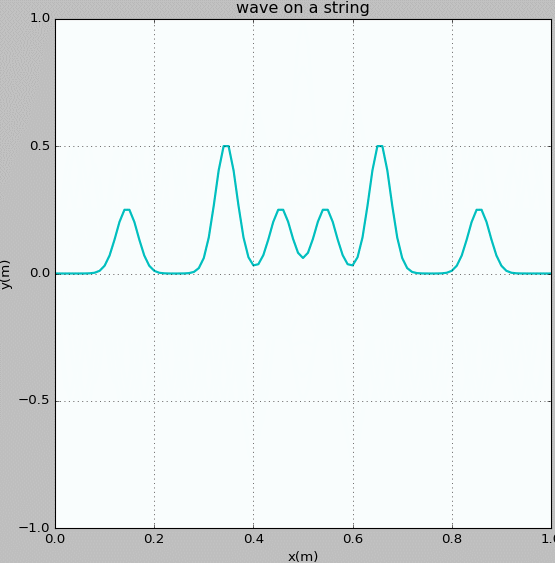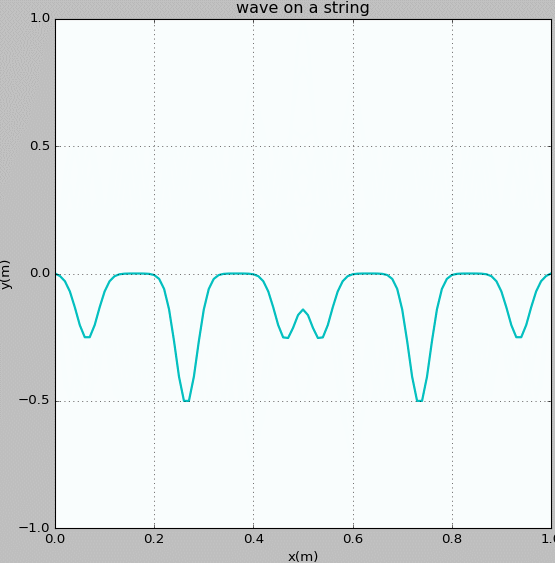
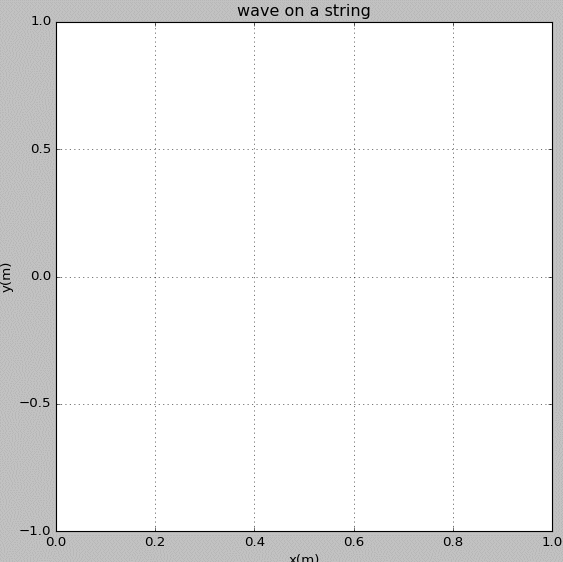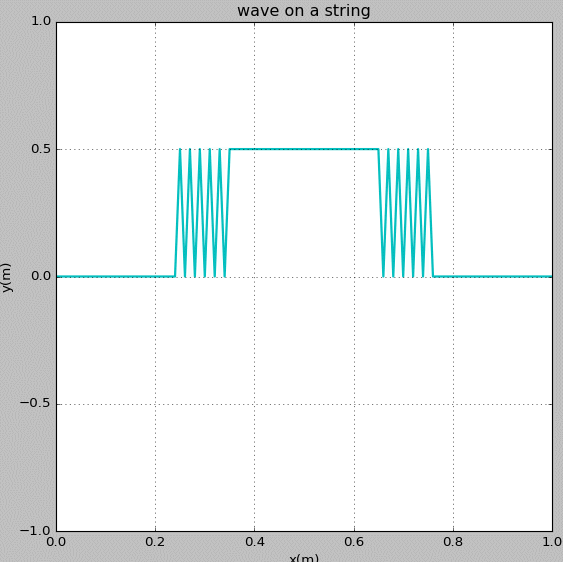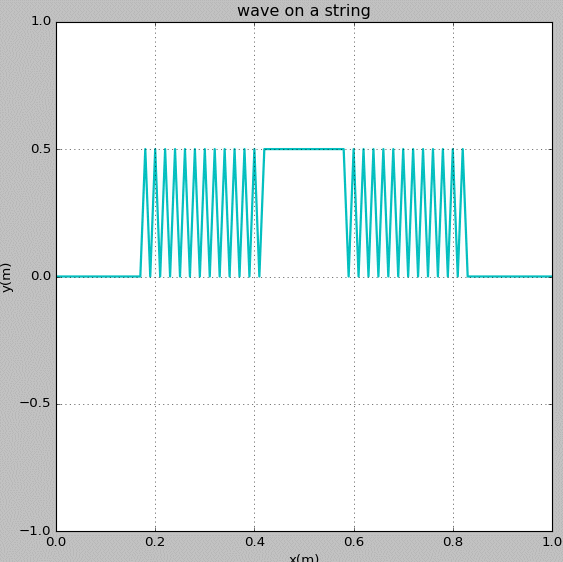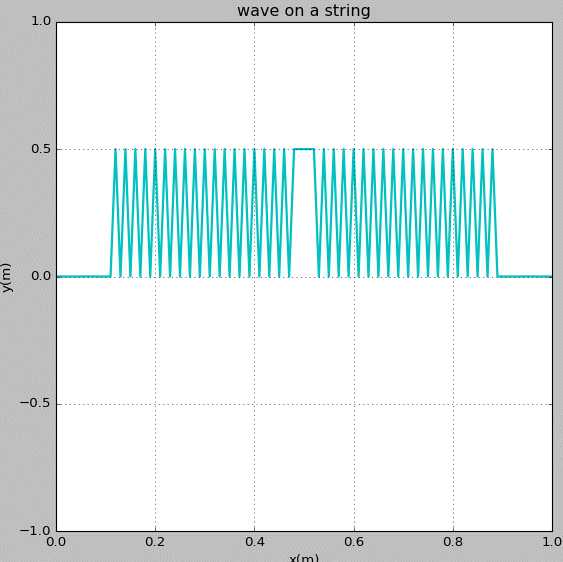
Figure 6: Waves propagating on a string with fixed ends. The initial pluck is a square wave.
Figure 7: Slow playback of Figure 6.
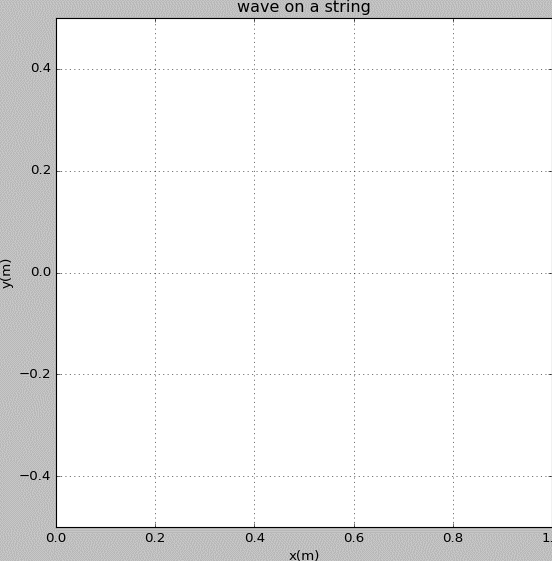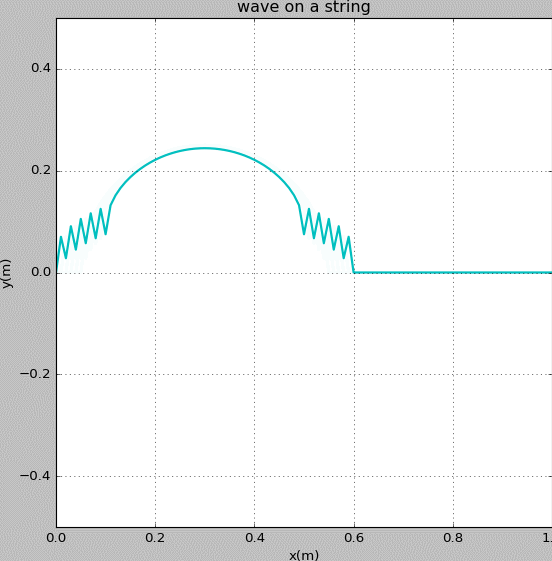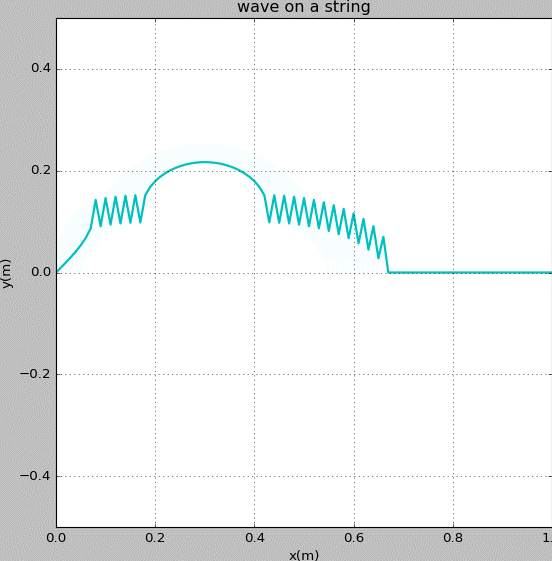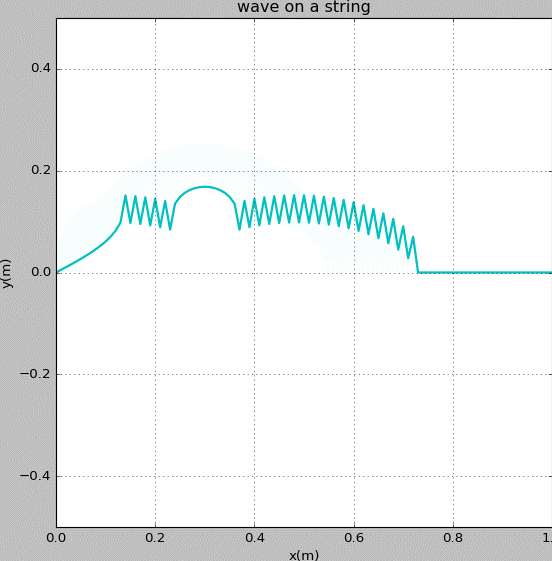
Figure 8: Waves propagating on a string with fixed ends. The initial pluck is a triangle wave whose top is at x = 0.5 m.
Figure 9: Waves propagating on a string with fixed ends. The initial pluck is a right triangle wave whose top is at x = 0.25 m.
Figure 10: Slow playback of Figure 9.
§ 3.2.2 Results for the string signal of waves on strings excited with different initial plucks
The displacement at a distance of 5 percent from one end was recorded.
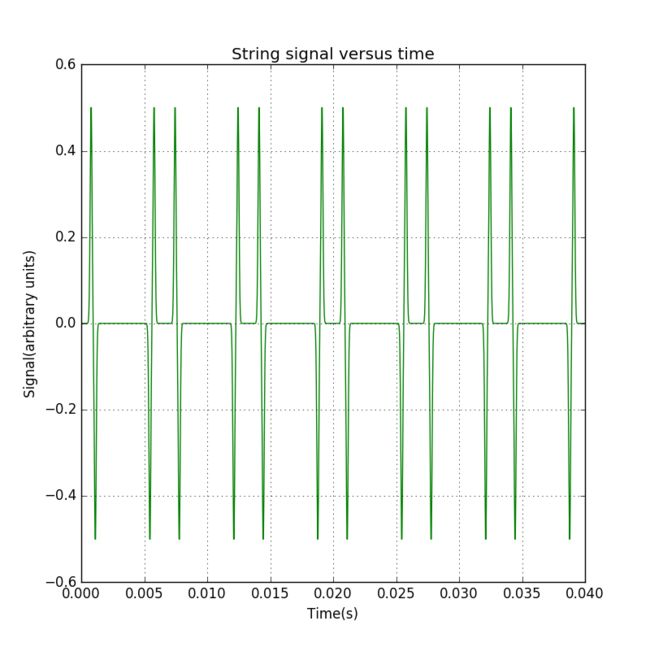
Figure 11: Signal from a vibrating string. The string was excited with one Gaussian initial pluck centered at x = 0.3 m.
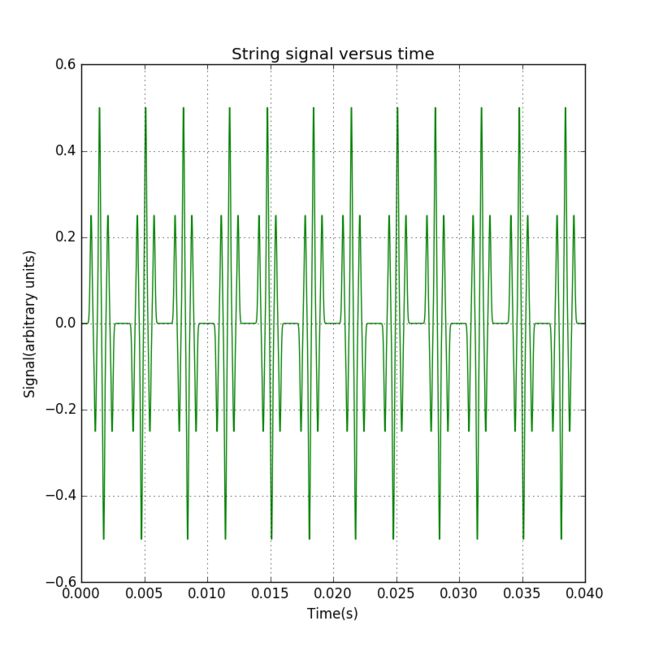
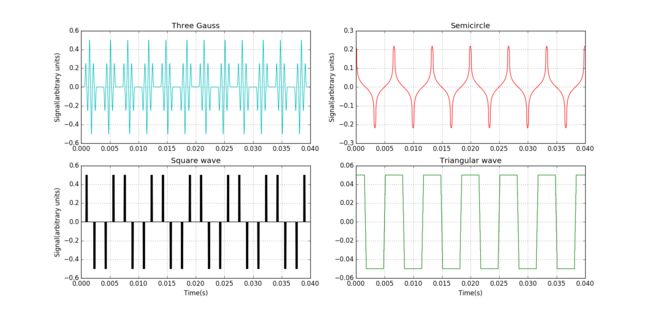
Figure 12: Signal from a vibrating string. The string was excited with three Gaussian initial plucks centered at x = 0.3 m, 0.5 m, and 0.7 m.
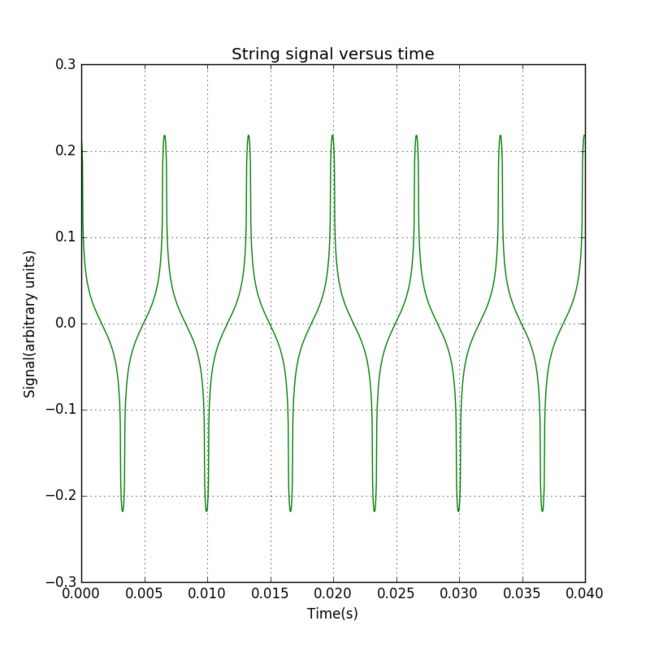
Figure 13: Signal from a vibrating string. The string was excited with a semicicular initial plucks centered at the middle of the string.
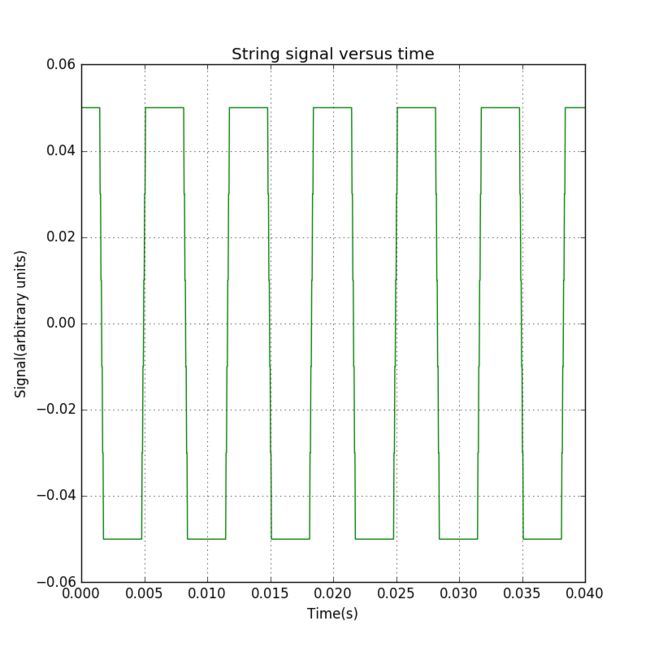
Figure 14: Signal from a vibrating string. The string was excited with a square initial plucks centered at the middle of the string.
Figure 15: Signal from a vibrating string. The string was excited with a triangle initial plucks centered at the middle of the string.
Figure 16: Gathering of the four figures above.
§ 3.2.2 Results for power spectrum of the string signal of waves on strings excited with different initial plucks
Here are the power spectrum of the string signal of waves on strings excited with different initial plucks at a distance of 5 percent from one end .
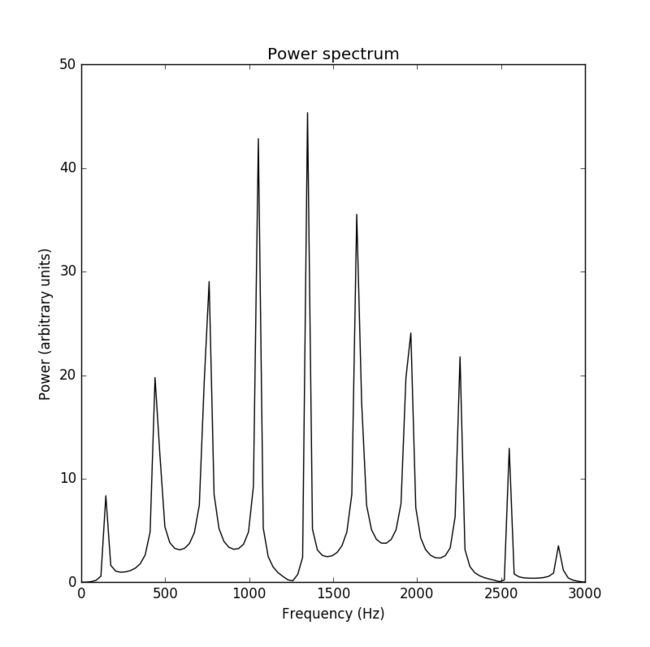
Figure 17: Power spectrum of the signal from a vibrating string. The string was excited with a Gaussian initial pluck centered at the middle of the string.
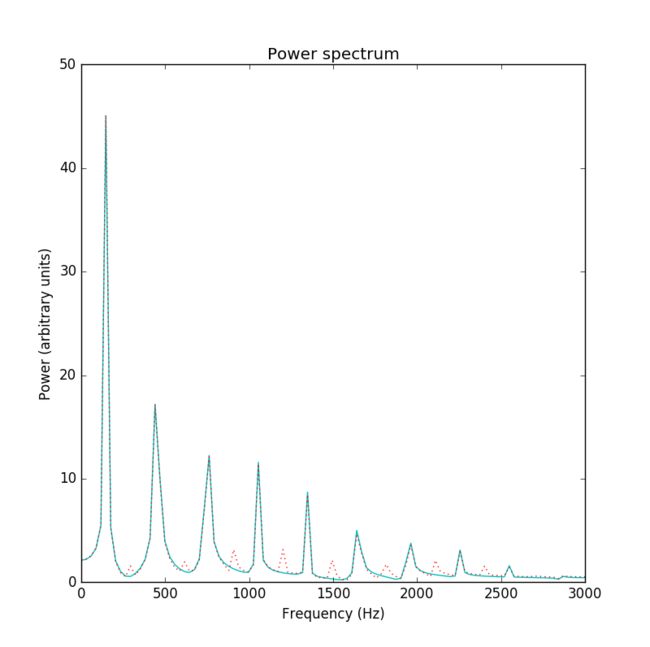
Figure 18: Power spectrum of the signal from a vibrating string. The string was excited with a Guassian inital pluck. The dotted curve is the power spectrum obtained when the string was excited 5 percent from its center. For comparison, the solid curve shows the power spectrum found when the string was excited at the centered.
Figure 19: Power spectrum of the signal from a vibrating string. The string was excited with a semicircular inital pluck. The dotted curve is the power spectrum obtained when the string was excited 1 percent from its center. For comparison, the solid curve shows the power spectrum found when the string was excited at the centered.
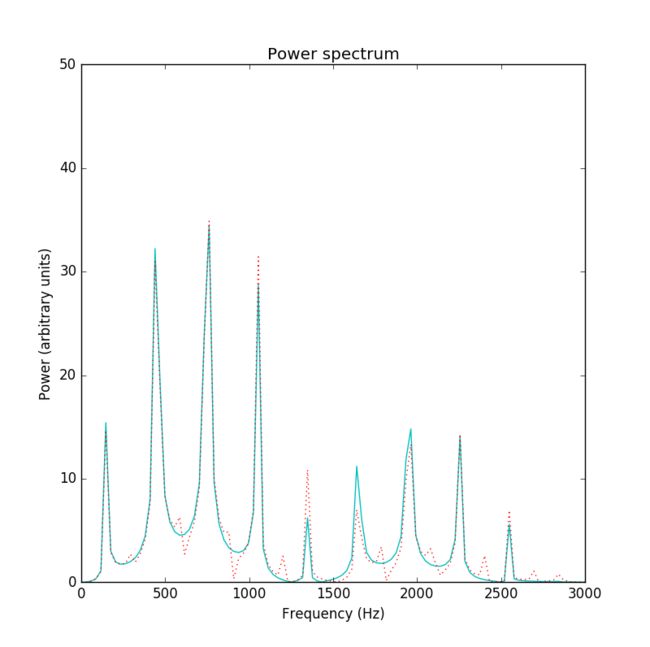
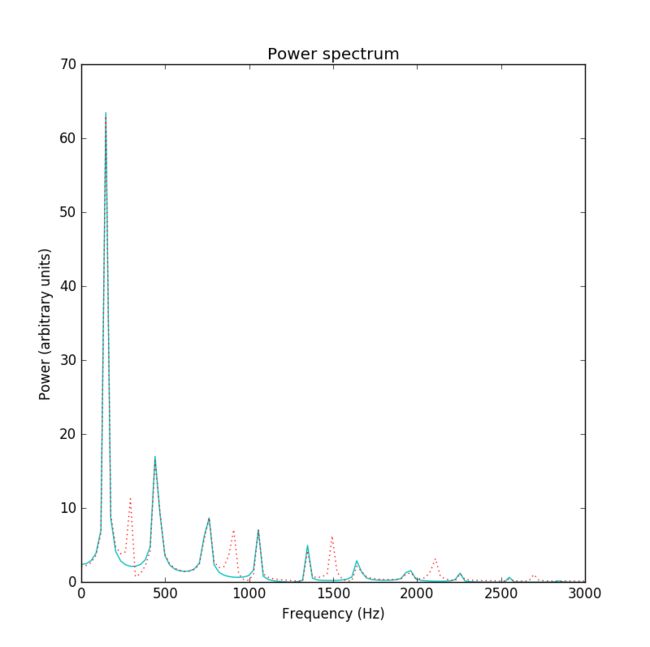
Figure 20: Power spectrum of the signal from a vibrating string. The string was excited with a square inital pluck. The dotted curve is the power spectrum obtained when the string was excited 5 percent from its center. For comparison, the solid curve shows the power spectrum found when the string was excited at the centered.
Figure 21: Power spectrum of the signal from a vibrating string. The string was excited with a square inital pluck. The dotted curve is the power spectrum obtained when the string was excited 5 percent from its center. For comparison, the solid curve shows the power spectrum found when the string was excited at the centered.
Figure 22: Gathering of the four figures above.
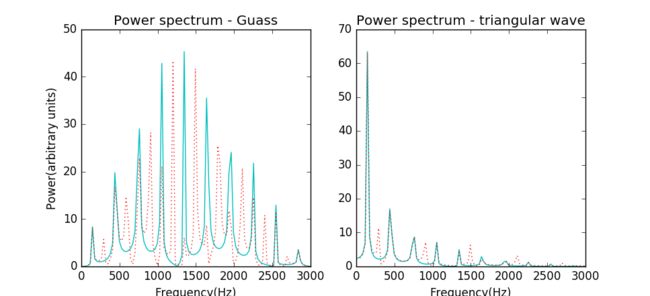
As our problem demands, here is the comparison of the power spectrum for a string excited realistically with the results found for a Gaussian initial wavepacket.
Figure 23: Left: the power for a string excited realistically. Right: the power spectrum for a string excited with a Gaussian initial wavepacket.
4. Conclusion
- All the conclusions can be derived from the figures above.
5. Acknowledgement
- Prof. Cai
- Wikipedia
- Baidu
- Wu Yuqiao
- TS (Tan Shan)