在之前一个老师的安利下,还是开了这个博弈论的坑。书是:
这本书本身写的非常棒,而且很易懂,强烈安利。
顺便自己记录下读书的笔记和一些想法,同时也把书中比较难理解的地方用自己的理解说一下,希望能帮到大家。
第一章 1完全信息静态博弈
在本章,我们来讨论如下简单形式的博弈(包含如下特点):
- 静态博弈:所有游戏的参与者同时选择行动,然后根据行动每个参与者得到各自的结果
- 完全信息博弈:即每一个参与者的收益函数在所有参与者之间是共同知识,即不存在信息的不对称性,也就是说每个参与者对游戏规则以及游戏演化机理完全明白。
关于本章的结构:
在1.1节中我们先会介绍两个问题:
- 如何描述一个博弈问题
- 如何求得博弈问题的解
在1问题中我们定义了博弈的标准式表述和严格劣战略的概念,在2问题中我们根据前面的介绍引出了纳什均衡的概念。
在1.2节中我们会运用前面的工具来分析古诺(Cournot,1838)的不完全竞争模型,使用纳什均衡的方式对之进行求解,之后我们将重回理论知识,我们将会定义混合战略,它可以理解为一个参与者并不能确定其他参与者会如何行动时应该选的战略,之后会引出纳什定理。
1.1节博弈的标准式和纳什均衡
1.1.A 博弈的标准式表述
首先举一个大家都比较熟悉的、很经典的例子:囚徒困境
警方逮捕甲、乙两名嫌疑犯,但没有足够证据指控二人入罪。于是警方分开囚禁嫌疑犯,分别和二人见面,并向双方提供以下相同的选择: 若一人认罪并作证检控对方(相关术语称“背叛”对方),而对方保持沉默,此人将即时获释,沉默者将判监10年。若二人都保持沉默(相关术语称互相“合作”),则二人同样判监1年。 若二人都互相检举(相关术语称互相“背叛”),则二人同样判监8年。
对于这个博弈我们可以来使用如下矩阵来进行描述
对于这个矩阵,其横纵轴分别为囚徒1、2所对应的选择。方框里的值第一项代表在此选择下,囚徒1 的收益情况,第二项代表囚徒2的收益情况。
现在我们回到一般情况,对于一个博弈的标准式,我们对之的表述包括以下几方面:
- 博弈的参与者(例子中的囚徒1和囚徒2)
- 每一个参与者可供选择的战略集(例子中的沉默和招认)
- 针对所有参与者可选择的的战略组合得到每一个参与者的收益(例子中方框中的值)
那么我们就可以对一个博弈给出如下定义:
定义 在一个n个人的博弈的标准式表述中,参与者的战略空间为S1, S2,……, Sn(Si表示第i个人的可选择战略集),si 收益函数为u1,u2……,un,ui(si,……sn),即参与者选择策略(si,……sn)时,第i个人的收益,我们用
来表示此博弈。
当然此博弈的标准式不仅仅可以表达静态完全信息博弈(尽管我们的例子是如此),在后面的动态问题中也可以用到,不过分析动态问题时我们可能更常用它的一种变式——
博弈的扩展式,不过这都是后话了。
1.1. B重复剔除严格劣战略
在这一节我们来着手对一个博弈进行分析,还是那个囚徒困境的例子:
对于囚徒1,他选择不同战略的时候,收益如下:
选择沉默:{-1,-9}(当囚徒2选择沉默的时收益为-1,选择招认的时收益为-9)
选择招认:{0,-6}(当囚徒2选择沉默的时收益为-1,选择招认的时收益为-9)
对于囚徒2,其不同战略得到的收益与囚徒1 相同。
而至此,我们可以看到,选择沉默时{-1,-9},招认时{0,-6},对于任何一个囚徒,其选择沉默时不管对方选择任何战略,自己的收益都没有选择招认时的收益高。对于这个博弈中,对于囚徒1、2选择沉默都是严格劣战略。
我们将这个结论一般化:
对其他参与者在其战略空间 中每一组可能的战略 都成立。
使用重复剔除严格劣战略的方法解博弈问题
对于如下博弈:
| 参与人1 |
参与人2 |
|||
|
|
左 |
中 |
右 |
|
| 上 |
1,0 |
1,2 |
0,1 |
|
| 下 |
0,3 |
0,1 |
2,0 |
|
我们先寻找参与人1和参与人2的严格劣战略:
首先,对于参与人1来说,明显,上下都不是严格占优的,(因为无法确定参与人2到底会选择哪个),但是对于参与人2来说,右是严格劣于中的(2>1,1>0)所以判断是可以将右在参与人2的策略中剔除。
| 参与人1 |
参与人2 |
|||
|
|
左 |
中 |
|
|
| 上 |
1,0 |
1,2 |
||
| 下 |
0,3 |
0,1 |
||
之后再对参与人1进行剔除严格劣战略:
在这种情况下,对于参与人1,下是严格劣于上的,删除下策略
| 参与人1 |
参与人2 |
|||
|
|
左 |
中 |
|
|
| 上 |
1,0 |
1,2 |
||
同理再进行剔除一次,可以将参与人2 的左战略删除,我们得到本次博弈的结果(上,中)。
对于重复剔除严格劣战略,有着以下几点缺点:
- 这个战略建立的一个大的基础就是参与者双方必须完全理性,并且双方知道对方完全理性,并且双方遵守“完全理性”的规则。
- 对于一些博弈,是无法找到并剔除完全劣战略的(不存在完全劣战略)
1.1. c纳什均衡的引入
在一个博弈中,假设参与者全是理性人,倘若这个博弈有唯一解,即这个博弈处于以下的状态:每个人在这种状态下,自己的策略都优于(至少是不劣于)其他可选择的策略,即达到一个共赢的状态,把这个状态就叫做纳什均衡。
和纳什均衡相关的一个东西叫做协议理念:倘若多个参与者在一个博弈中要达成某项协议,那么这个协议对于每个参与者来说都应该是最优的(至少不劣于其他策略),这个协议才没有人去违反。达成这个协议的状态可以简单的理解为纳什均衡。
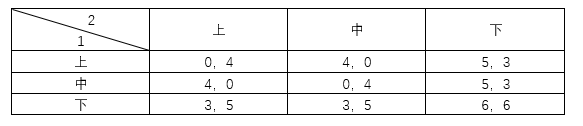
下面给出一个纳什均衡的例子:
同样,囚徒困境和本文中举的第二个例子也能用纳什均衡来求解,这里就不一一列出。在这个,纳什均衡为(下,下)因为对这个战略组合来说,当1选择下的时候,2 的最优选择也是下,当2 选择下的时候,1的最优选择也是下,这就达到了纳什均衡。举个反例,当1选择上的时候,2的最优选择为上,而当2选择为上的时候,1的最优选择变成了中,这个时候就没有处于平衡状态,双方策略会发生改变直至达到纳什均衡。
对于某些博弈会存在多个纳什均衡,比较简单的例子就是把上面那个例子中,(上,下)
对应的值改为6,6
这个时候就会产生多个纳什均衡,当然还会有不存在纳什均衡的情况,这些情况会在后续章节讨论。