使用 Hyperopt 进行参数调优（译）

本文是对Parameter Tuning with Hyperopt一文的翻译。译者在设计深度学习模型的网络结构发现了hyperopt这个大杀器，相比每次手动各种试，用工具批量调节网络中的各种超参数确实能省心不少。不过hyperopt的官方文档描述的太渣，google 了一翻，发现这篇博客算是介绍的比较清楚的一个，便顺手翻译了，译文已取得原作者授权。

正文开始

本文将介绍一种快速有效的方法用于实现机器学习模型的调参。有两种常用的调参方法：网格搜索和随机搜索。每一种都有自己的优点和缺点。网格搜索速度慢，但在搜索整个搜索空间方面效果很好，而随机搜索很快，但可能会错过搜索空间中的重要点。幸运的是，还有第三种选择：贝叶斯优化。本文我们将重点介绍贝叶斯优化的一个实现，一个名为hyperopt的 Python 模块。

使用贝叶斯优化进行调参可以让我们获得给定模型的最佳参数，例如逻辑回归模型。这也使我们能够执行最佳的模型选择。通常机器学习工程师或数据科学家将为少数模型（如决策树，支持向量机和 K 近邻）执行某种形式（网格搜索或随机搜索）的手动调参，然后比较准确率并选择最佳的一个来使用。该方法可能比较的是次优模型。也许数据科学家找到了决策树的最优参数，但却错过了 SVM 的最优参数。这意味着他们的模型比较是有缺陷的。如果 SVM 参数调整得很差，K 近邻可能每次都会击败 SVM。贝叶斯优化允许数据科学家找到所有模型的最佳参数，并因此比较最佳模型。这会得到更好的模型选择，因为你比较的是最佳的 k 近邻和最佳的决策树。只有这样你才能非常自信地进行模型选择，确保选择并使用的是实际最佳的模型。

本文涵盖的主题有：

目标函数
搜索空间
存储评估试验
可视化
经典数据集上的完整示例：Iris

要使用下面的代码，你必须安装hyperopt和pymongo

目标函数 - 一个启发性例子

假设你有一个定义在某个范围内的函数，并且想把它最小化。也就是说，你想找到产生最低输出值的输入值。下面的简单例子找到x的值用于最小化线性函数y(x) = x

from hyperopt import fmin, tpe, hp
best = fmin(
    fn=lambda x: x,
    space=hp.uniform('x', 0, 1),
    algo=tpe.suggest,
    max_evals=100)
print best

我们来分解一下这个例子。

函数fmin首先接受一个函数来最小化，记为fn，在这里用一个匿名函数lambda x: x来指定。该函数可以是任何有效的值返回函数，例如回归中的平均绝对误差。

下一个参数指定搜索空间，在本例中，它是0到1之间的连续数字范围，由hp.uniform('x', 0, 1)指定。hp.uniform是一个内置的hyperopt函数，它有三个参数：名称x，范围的下限和上限0和1。

algo参数指定搜索算法，本例中tpe表示 tree of Parzen estimators。该主题超出了本文的范围，但有数学背景的读者可以细读这篇文章。algo参数也可以设置为hyperopt.random，但是这里我们没有涉及，因为它是众所周知的搜索策略。但在未来的文章中我们可能会涉及。

最后，我们指定fmin函数将执行的最大评估次数max_evals。这个fmin函数将返回一个python字典。

上述函数的一个输出示例是{'x': 0.000269455723739237}。

以下是该函数的图。红点是我们试图找到的点。

Silvrback blog image

更复杂的例子

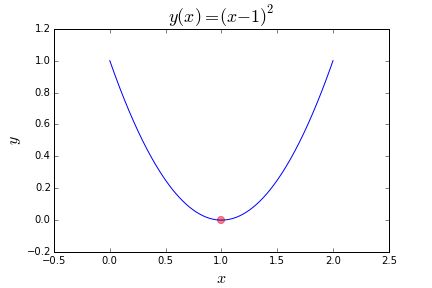
这有一个更复杂的目标函数：lambda x: (x-1)**2。这次我们试图最小化一个二次方程y(x)=(x-1)**2。所以我们改变搜索空间以包括我们已知的最优值（x=1）加上两边的一些次优范围：hp.uniform('x', -2, 2)。

现在我们有：

best = fmin(
    fn=lambda x: (x-1)**2,
    space=hp.uniform('x', -2, 2),
    algo=tpe.suggest,
    max_evals=100)
print best

输出应该看起来像这样：

{'x': 0.997369045274755}

这是函数图。

Silvrback blog image

有时也许我们想要最大化目标函数，而不是最小化它。为此，我们只需要返回函数的负数。例如，我们有函数y(x) = -(x**2)：

Silvrback blog image

我们如何解决这个问题？我们采用目标函数lambda x: -(x**2)并返回负值，只需给出lambda x: -1*-(x**2)或者lambda x: (x**2)即可。

这里有一个和例子1类似，但我们不是最小化，而是试图最大化。

Silvrback blog image

这里有许多（无限多且无限范围）局部最小值的函数，我们也试图将其最大化：

Silvrback blog image

搜索空间

hyperopt模块包含一些方便的函数来指定输入参数的范围。我们已经见过hp.uniform。最初，这些是随机搜索空间，但随着hyperopt更多的学习（因为它从目标函数获得更多反馈），通过它认为提供给它最有意义的反馈，会调整并采样初始搜索空间的不同部分。

以下内容将在本文中使用：

hp.choice(label, options) 其中options应是 python 列表或元组。
hp.normal(label, mu, sigma) 其中mu和sigma分别是均值和标准差。
hp.uniform(label, low, high) 其中low和high是范围的下限和上限。

其他也是可用的，例如hp.normal，hp.lognormal，hp.quniform，但我们不会在这里使用它们。

为了查看搜索空间的一些例子，我们应该导入另一个函数，同时定义搜索空间。

import hyperopt.pyll.stochastic

space = {
    'x': hp.uniform('x', 0, 1),
    'y': hp.normal('y', 0, 1),
    'name': hp.choice('name', ['alice', 'bob']),
}

print hyperopt.pyll.stochastic.sample(space)

一个示例输出是：

{'y': -1.4012610048810574, 'x': 0.7258615424906184, 'name': 'alice'}

尝试运行几次并查看不同的样本。

通过 Trials 捕获信息

如果能看到hyperopt黑匣子内发生了什么是极好的。Trials对象使我们能够做到这一点。我们只需要导入一些东西。

from hyperopt import fmin, tpe, hp, STATUS_OK, Trials

fspace = {
    'x': hp.uniform('x', -5, 5)
}

def f(params):
    x = params['x']
    val = x**2
    return {'loss': val, 'status': STATUS_OK}

trials = Trials()
    best = fmin(fn=f, space=fspace, algo=tpe.suggest, max_evals=50, trials=trials)

print 'best:', best

print 'trials:'
for trial in trials.trials[:2]:
    print trial

STATUS_OK和Trials是新导入的。Trials对象允许我们在每个时间步存储信息。然后我们可以将它们打印出来，并在给定的时间步查看给定参数的函数评估值。

这是上面代码的一个输出示例：

best: {'x': 0.014420181637303776}
trials:
{'refresh_time': None, 'book_time': None, 'misc': {'tid': 0, 'idxs': {'x': [0]}, 'cmd': ('domain_attachment', 'FMinIter_Domain'), 'vals': {'x': [1.9646918559786162]}, 'workdir': None}, 'state': 2, 'tid': 0, 'exp_key': None, 'version': 0, 'result': {'status': 'ok', 'loss': 3.8600140889486996}, 'owner': None, 'spec': None}
{'refresh_time': None, 'book_time': None, 'misc': {'tid': 1, 'idxs': {'x': [1]}, 'cmd': ('domain_attachment', 'FMinIter_Domain'), 'vals': {'x': [-3.9393509404526728]}, 'workdir': None}, 'state': 2, 'tid': 1, 'exp_key': None, 'version': 0, 'result': {'status': 'ok', 'loss': 15.518485832045357}, 'owner': None, 'spec': None}

Trials对象将数据存储为BSON对象，其工作方式与JSON对象相同。BSON来自pymongo模块。我们不会在这里讨论细节，这是对于需要使用MongoDB进行分布式计算的hyperopt的高级选项，因此需要导入pymongo。回到上面的输出。tid是时间 id，即时间步，其值从0到max_evals-1。它随着迭代次数递增。'x'是键'vals'的值，其中存储的是每次迭代参数的值。'loss'是键'result'的值，其给出了该次迭代目标函数的值。

我们用另一种方式来看看。

可视化

我们将在这里讨论两种类型的可视化：值 vs. 时间与损失 vs. 值。首先是值 vs. 时间。以下是绘制上述Trial.trials数据的代码和示例输出。

f, ax = plt.subplots(1)
xs = [t['tid'] for t in trials.trials]
ys = [t['misc']['vals']['x'] for t in trials.trials]
ax.set_xlim(xs[0]-10, xs[-1]+10)
ax.scatter(xs, ys, s=20, linewidth=0.01, alpha=0.75)
ax.set_title('$x$ $vs$ $t$ ', fontsize=18)
ax.set_xlabel('$t$', fontsize=16)
ax.set_ylabel('$x$', fontsize=16)

假设我们将`max_evals设为1000，输出应该如下所示。

[图片上传失败...(image-2f30d5-1524930959800)]

我们可以看到，最初算法从整个范围中均匀地选择值，但随着时间的推移以及参数对目标函数的影响了解越来越多，该算法越来越聚焦于它认为会取得最大收益的区域-一个接近零的范围。它仍然探索整个解空间，但频率有所下降。

现在让我们看看损失 vs. 值的图。

f, ax = plt.subplots(1)
xs = [t['misc']['vals']['x'] for t in trials.trials]
ys = [t['result']['loss'] for t in trials.trials]
ax.scatter(xs, ys, s=20, linewidth=0.01, alpha=0.75)
ax.set_title('$val$ $vs$ $x$ ', fontsize=18)
ax.set_xlabel('$x$', fontsize=16)
ax.set_ylabel('$val$', fontsize=16)

Silvrback blog image

它给了我们所期望的，因为函数y(x)=x**2是确定的。

总结一下，让我们尝试一个更复杂的例子，伴随更多的随机性和更多的参数。

Iris 数据集

在本节中，我们将介绍4个使用hyperopt在经典数据集 Iris 上调参的完整示例。我们将涵盖 K 近邻（KNN），支持向量机（SVM），决策树和随机森林。需要注意的是，由于我们试图最大化交叉验证的准确率（acc请参见下面的代码），而hyperopt只知道如何最小化函数，所以必须对准确率取负。最小化函数f与最大化f的负数是相等的。

对于这项任务，我们将使用经典的Iris数据集，并进行一些有监督的机器学习。数据集有有4个输入特征和3个输出类别。数据被标记为属于类别0，1或2，其映射到不同种类的鸢尾花。输入有4列：萼片长度，萼片宽度，花瓣长度和花瓣宽度。输入的单位是厘米。我们将使用这4个特征来学习模型，预测三种输出类别之一。因为数据由sklearn提供，它有一个很好的DESCR属性，可以提供有关数据集的详细信息。尝试以下代码以获得更多细节信息。

print iris.feature_names # input names
print iris.target_names # output names
print iris.DESCR # everything else

让我们通过使用下面的代码可视化特征和类来更好地了解数据。如果你还没安装别忘了先执行pip install searborn。

import seaborn as sns
sns.set(style="whitegrid", palette="husl")

iris = sns.load_dataset("iris")
print iris.head()

iris = pd.melt(iris, "species", var_name="measurement")
print iris.head()

f, ax = plt.subplots(1, figsize=(15,10))
sns.stripplot(x="measurement", y="value", hue="species", data=iris, jitter=True, edgecolor="white", ax=ax)

这是图表：

Silvrback blog image

K 近邻

我们现在将使用hyperopt来找到 K近邻（KNN）机器学习模型的最佳参数。KNN 模型是基于训练数据集中 k 个最近数据点的大多数类别对来自测试集的数据点进行分类。关于这个算法的更多信息可以参考这里。下面的代码结合了我们所涵盖的一切。

from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target

def hyperopt_train_test(params):
    clf = KNeighborsClassifier(**params)
    return cross_val_score(clf, X, y).mean()

space4knn = {
    'n_neighbors': hp.choice('n_neighbors', range(1,100))
}

def f(params):
    acc = hyperopt_train_test(params)
    return {'loss': -acc, 'status': STATUS_OK}

trials = Trials()
best = fmin(f, space4knn, algo=tpe.suggest, max_evals=100, trials=trials)
print 'best:'
print best

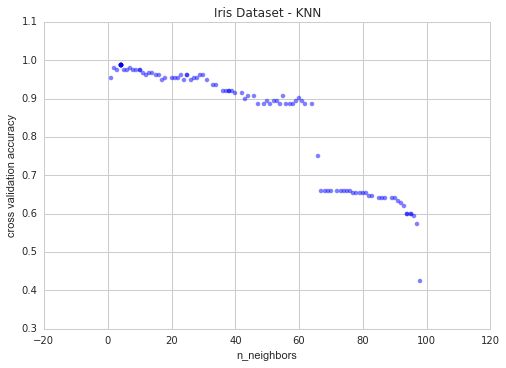
现在让我们看看输出结果的图。y轴是交叉验证分数，x轴是 k 近邻个数。下面是代码和它的图像：

f, ax = plt.subplots(1)#, figsize=(10,10))
xs = [t['misc']['vals']['n'] for t in trials.trials]
ys = [-t['result']['loss'] for t in trials.trials]
ax.scatter(xs, ys, s=20, linewidth=0.01, alpha=0.5)
ax.set_title('Iris Dataset - KNN', fontsize=18)
ax.set_xlabel('n_neighbors', fontsize=12)
ax.set_ylabel('cross validation accuracy', fontsize=12)

Silvrback blog image

k 大于63后，准确率急剧下降。这是因为数据集中每个类的数量。这三个类中每个类只有50个实例。所以让我们将'n_neighbors'的值限制为较小的值来进一步探索。

from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target

def hyperopt_train_test(params):
    clf = KNeighborsClassifier(**params)
    return cross_val_score(clf, X, y).mean()

space4knn = {
    'n_neighbors': hp.choice('n_neighbors', range(1,50))
}

def f(params):
    acc = hyperopt_train_test(params)
    return {'loss': -acc, 'status': STATUS_OK}

trials = Trials()
best = fmin(f, space4knn, algo=tpe.suggest, max_evals=100, trials=trials)
print 'best:'
print best

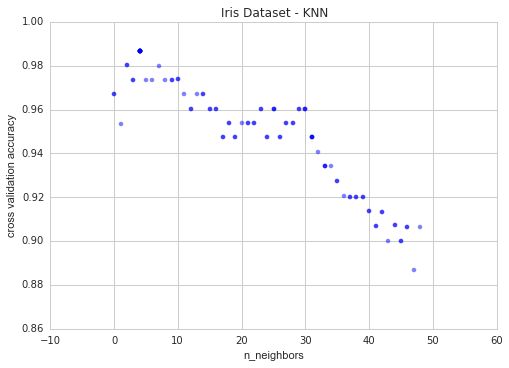
这是我们运行相同的可视化代码得到的结果：

Silvrback blog image

现在我们可以清楚地看到k有一个最佳值，k=4。

上面的模型没有做任何预处理。所以我们来归一化和缩放特征，看看是否有帮助。用如下代码：

# now with scaling as an option
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target

def hyperopt_train_test(params):
    X_ = X[:]

    if 'normalize' in params:
        if params['normalize'] == 1:
            X_ = normalize(X_)
            del params['normalize']

    if 'scale' in params:
        if params['scale'] == 1:
            X_ = scale(X_)
            del params['scale']

    clf = KNeighborsClassifier(**params)
    return cross_val_score(clf, X_, y).mean()

space4knn = {
    'n_neighbors': hp.choice('n_neighbors', range(1,50)),
    'scale': hp.choice('scale', [0, 1]),
    'normalize': hp.choice('normalize', [0, 1])
}

def f(params):
    acc = hyperopt_train_test(params)
    return {'loss': -acc, 'status': STATUS_OK}

trials = Trials()
best = fmin(f, space4knn, algo=tpe.suggest, max_evals=100, trials=trials)
print 'best:'
print best

并像这样绘制参数：

parameters = ['n_neighbors', 'scale', 'normalize']
cols = len(parameters)
f, axes = plt.subplots(nrows=1, ncols=cols, figsize=(15,5))
cmap = plt.cm.jet
for i, val in enumerate(parameters):
    xs = np.array([t['misc']['vals'][val] for t in trials.trials]).ravel()
    ys = [-t['result']['loss'] for t in trials.trials]
    xs, ys = zip(\*sorted(zip(xs, ys)))
    ys = np.array(ys)
    axes[i].scatter(xs, ys, s=20, linewidth=0.01, alpha=0.75, c=cmap(float(i)/len(parameters)))
    axes[i].set_title(val)

Silvrback blog image

我们看到缩放和/或归一化数据并不会提高预测准确率。k的最佳值仍然为4，这得到98.6％的准确率。

所以这对于简单模型 KNN 调参很有用。让我们看看用支持向量机（SVM）能做什么。

支持向量机（SVM）

由于这是一个分类任务，我们将使用sklearn的SVC类。代码如下：

iris = datasets.load_iris()
X = iris.data
y = iris.target

def hyperopt_train_test(params):
    X_ = X[:]

    if 'normalize' in params:
        if params['normalize'] == 1:
            X_ = normalize(X_)
            del params['normalize']

    if 'scale' in params:
        if params['scale'] == 1:
            X_ = scale(X_)
            del params['scale']

    clf = SVC(**params)
    return cross_val_score(clf, X_, y).mean()

space4svm = {
    'C': hp.uniform('C', 0, 20),
    'kernel': hp.choice('kernel', ['linear', 'sigmoid', 'poly', 'rbf']),
    'gamma': hp.uniform('gamma', 0, 20),
    'scale': hp.choice('scale', [0, 1]),
    'normalize': hp.choice('normalize', [0, 1])
}

def f(params):
    acc = hyperopt_train_test(params)
    return {'loss': -acc, 'status': STATUS_OK}

trials = Trials()
best = fmin(f, space4svm, algo=tpe.suggest, max_evals=100, trials=trials)
print 'best:'
print best

parameters = ['C', 'kernel', 'gamma', 'scale', 'normalize']
cols = len(parameters)
f, axes = plt.subplots(nrows=1, ncols=cols, figsize=(20,5))
cmap = plt.cm.jet
for i, val in enumerate(parameters):
    xs = np.array([t['misc']['vals'][val] for t in trials.trials]).ravel()
    ys = [-t['result']['loss'] for t in trials.trials]
    xs, ys = zip(\*sorted(zip(xs, ys)))
    axes[i].scatter(xs, ys, s=20, linewidth=0.01, alpha=0.25, c=cmap(float(i)/len(parameters)))
    axes[i].set_title(val)
    axes[i].set_ylim([0.9, 1.0])

这是我们得到的：

Silvrback blog image

同样，缩放和归一化也没有帮助。核函数的首选是（linear），C的最佳值是1.4168540399911616，gamma的最佳值是15.04230279483486。这组参数得到了99.3％的分类准确率。

决策树

我们将尝试只优化决策树的一些参数。代码如下。

iris = datasets.load_iris()
X_original = iris.data
y_original = iris.target

def hyperopt_train_test(params):
    X_ = X[:]
    if 'normalize' in params:
        if params['normalize'] == 1:
            X_ = normalize(X_)
            del params['normalize']

    if 'scale' in params:
        if params['scale'] == 1:
            X_ = scale(X_)
            del params['scale']
    clf = DecisionTreeClassifier(**params)
    return cross_val_score(clf, X, y).mean()

space4dt = {
    'max_depth': hp.choice('max_depth', range(1,20)),
    'max_features': hp.choice('max_features', range(1,5)),
    'criterion': hp.choice('criterion', ["gini", "entropy"]),
    'scale': hp.choice('scale', [0, 1]),
    'normalize': hp.choice('normalize', [0, 1])
}

def f(params):
acc = hyperopt_train_test(params)
return {'loss': -acc, 'status': STATUS_OK}

trials = Trials()
best = fmin(f, space4dt, algo=tpe.suggest, max_evals=300, trials=trials)
print 'best:'
print best

输出如下，其准确率为97.3％。

{'max_features': 1, 'normalize': 0, 'scale': 0, 'criterion': 0, 'max_depth': 17}

以下是图表。我们可以看到，对于不同的scale值，normalize和criterion，性能几乎没有差别。

parameters = ['max_depth', 'max_features', 'criterion', 'scale', 'normalize'] # decision tree
cols = len(parameters)
f, axes = plt.subplots(nrows=1, ncols=cols, figsize=(20,5))
cmap = plt.cm.jet
for i, val in enumerate(parameters):
    xs = np.array([t['misc']['vals'][val] for t in trials.trials]).ravel()
    ys = [-t['result']['loss'] for t in trials.trials]
    xs, ys = zip(\*sorted(zip(xs, ys)))
    ys = np.array(ys)
    axes[i].scatter(xs, ys, s=20, linewidth=0.01, alpha=0.5, c=cmap(float(i)/len(parameters)))
    axes[i].set_title(val)
    #axes[i].set_ylim([0.9,1.0])

Silvrback blog image

随机森林

让我们来看看集成分类器随机森林发生了什么，随机森林只是在不同分区数据上训练的决策树集合，每个分区都对输出类进行投票，并将绝大多数类的选择为预测。

iris = datasets.load_iris()
X_original = iris.data
y_original = iris.target

def hyperopt_train_test(params):
    X_ = X[:]
    if 'normalize' in params:
        if params['normalize'] == 1:
            X_ = normalize(X_)
            del params['normalize']

    if 'scale' in params:
        if params['scale'] == 1:
            X_ = scale(X_)
            del params['scale']
    clf = RandomForestClassifier(**params)
    return cross_val_score(clf, X, y).mean()

space4rf = {
    'max_depth': hp.choice('max_depth', range(1,20)),
    'max_features': hp.choice('max_features', range(1,5)),
    'n_estimators': hp.choice('n_estimators', range(1,20)),
    'criterion': hp.choice('criterion', ["gini", "entropy"]),
    'scale': hp.choice('scale', [0, 1]),
    'normalize': hp.choice('normalize', [0, 1])
}

best = 0
def f(params):
    global best
    acc = hyperopt_train_test(params)
    if acc > best:
    best = acc
    print 'new best:', best, params
    return {'loss': -acc, 'status': STATUS_OK}

trials = Trials()
best = fmin(f, space4rf, algo=tpe.suggest, max_evals=300, trials=trials)
print 'best:'
print best

同样，与决策树相同，我们仅得到97.3％的准确率。

这是绘制参数的代码：

parameters = ['n_estimators', 'max_depth', 'max_features', 'criterion', 'scale', 'normalize']
f, axes = plt.subplots(nrows=2, ncols=3, figsize=(15,10))
cmap = plt.cm.jet
for i, val in enumerate(parameters):
    print i, val
    xs = np.array([t['misc']['vals'][val] for t in trials.trials]).ravel()
    ys = [-t['result']['loss'] for t in trials.trials]
    xs, ys = zip(\*sorted(zip(xs, ys)))
    ys = np.array(ys)
    axes[i/3,i%3].scatter(xs, ys, s=20, linewidth=0.01, alpha=0.5, c=cmap(float(i)/len(parameters)))
    axes[i/3,i%3].set_title(val)
    #axes[i/3,i%3].set_ylim([0.9,1.0])

Silvrback blog image

是时候把所有东西合为一体了

自动调整一个模型的参数（如SVM或KNN）非常有趣并且具有启发性，但同时调整它们并取得全局最佳模型则更有用。这使我们能够一次比较所有参数和所有模型，因此为我们提供了最佳模型。代码如下：

digits = datasets.load_digits()
X = digits.data
y = digits.target
print X.shape, y.shape

def hyperopt_train_test(params):
    t = params['type']
    del params['type']
    if t == 'naive_bayes':
        clf = BernoulliNB(**params)
    elif t == 'svm':
        clf = SVC(**params)
    elif t == 'dtree':
        clf = DecisionTreeClassifier(**params)
    elif t == 'knn':
        clf = KNeighborsClassifier(**params)
    else:
        return 0
    return cross_val_score(clf, X, y).mean()

space = hp.choice('classifier_type', [
    {
        'type': 'naive_bayes',
        'alpha': hp.uniform('alpha', 0.0, 2.0)
    },
    {
        'type': 'svm',
        'C': hp.uniform('C', 0, 10.0),
        'kernel': hp.choice('kernel', ['linear', 'rbf']),
        'gamma': hp.uniform('gamma', 0, 20.0)
    },
    {
        'type': 'randomforest',
        'max_depth': hp.choice('max_depth', range(1,20)),
        'max_features': hp.choice('max_features', range(1,5)),
        'n_estimators': hp.choice('n_estimators', range(1,20)),
        'criterion': hp.choice('criterion', ["gini", "entropy"]),
        'scale': hp.choice('scale', [0, 1]),
        'normalize': hp.choice('normalize', [0, 1])
    },
    {
        'type': 'knn',
        'n_neighbors': hp.choice('knn_n_neighbors', range(1,50))
    }
])

count = 0
best = 0
def f(params):
    global best, count
    count += 1
    acc = hyperopt_train_test(params.copy())
    if acc > best:
        print 'new best:', acc, 'using', params['type']
        best = acc
    if count % 50 == 0:
        print 'iters:', count, ', acc:', acc, 'using', params
    return {'loss': -acc, 'status': STATUS_OK}

trials = Trials()
best = fmin(f, space, algo=tpe.suggest, max_evals=1500, trials=trials)
print 'best:'
print best

由于我们增加了评估数量，此代码需要一段时间才能运行完：max_evals=1500。当找到新的最佳准确率时，它还会添加到输出用于更新。好奇为什么使用这种方法没有找到前面的最佳模型：参数为kernel=linear，C=1.416，gamma=15.042的SVM。

总结

我们已经介绍了简单的例子，如最小化确定的线性函数，以及复杂的例子，如调整随机森林参数。hyperopt的官方文档在这里。另一篇有关 hyperopt 不错的博客位于 FastML 站点（译注：已无效）。hyperopt作者的SciPy会议论文是Hyperopt: A Python Library for Optimizing the Hyperparameters of Machine Learning Algorithms，伴随一起的视频教程。关于工程来龙去脉的更多技术处理细节可以参见Making a Science of Model Search。

本文的技术可以用于机器学习以外的许多领域，例如调整epsilon-greedy multi-armed bandit的epsilon参数，或将参数传递给图生成器以生成具有某些属性的合成网络。我们以后会写更多。

使用 Hyperopt 进行参数调优（译）

正文开始

目标函数 - 一个启发性例子

更复杂的例子

搜索空间

通过 Trials 捕获信息

可视化

Iris 数据集

K 近邻

支持向量机（SVM）

决策树

随机森林

是时候把所有东西合为一体了

总结

你可能感兴趣的:(使用 Hyperopt 进行参数调优（译）)